湖南省株洲市八校联盟2020-2021学年高一上学期数学期末考试试卷
试卷更新日期:2021-12-15 类型:期末考试
一、单选题
-
1. 与2021°终边相同的角是( )A、-111° B、-70° C、141° D、221°2. 已知集合 则 ( )A、 B、 C、 D、3. 命题:“ , ”的否定是( )A、 , B、 , C、 , D、 ,4. 若 ,则下面大小关系正确的是( )A、 B、 C、 D、5. 已知函数 满足 ,则函数 的图象大致为( )A、
 B、
B、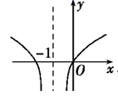 C、
C、 D、
D、 6. 设 ,则 的最小值为( )A、7 B、9 C、 D、7. 若角 的终边经过点 ,则 的值是( )A、 B、 C、 D、8. 已知函数 ,若 互不相等,且 ,则 的取值范围是( )A、 B、 C、 D、9. 已知函数 ,给出下述论述,其中正确的是( )A、当 时, 的定义域为 B、 一定有最小值 C、当 时, 的定义域为 D、若 在区间 上单调递增,则实数 的取值范围是
6. 设 ,则 的最小值为( )A、7 B、9 C、 D、7. 若角 的终边经过点 ,则 的值是( )A、 B、 C、 D、8. 已知函数 ,若 互不相等,且 ,则 的取值范围是( )A、 B、 C、 D、9. 已知函数 ,给出下述论述,其中正确的是( )A、当 时, 的定义域为 B、 一定有最小值 C、当 时, 的定义域为 D、若 在区间 上单调递增,则实数 的取值范围是二、多选题
-
10. 下列各组函数表示同一函数的是( )A、 , B、 , C、 , D、 ,11. 给出下列各命题,其中正确的是( )A、存在实数 ,使 B、要得到 的图像,只需把 向右平移 个单位 C、 是函数 图像的一条对称轴 D、函数 的图像恒过定点12. 已知 ,关于x的一元二次不等式 的解集中有且仅有3个整数,则a的值可以是( )A、5 B、6 C、7 D、8
三、填空题
-
13. 已知 ,则 .14. 已知函数 则 .15. 幂函数 在 上单调递增,则实数 .16. 若函数 是定义在实数集上的奇函数;则实数 ;满足关于 的不等式 恒成立,则实数 的取值范围.
四、解答题
-
17. 已知集合 , 或 .(1)、当 时,求 ;(2)、若 ,且“ ”是“ ”的充分不必要条件,求实数a的取值范围.18.(1)、化简求值:(2)、已知 , , , 为锐角,求 的值.19. 已知函数 ,求:(1)、 的最小正周期;(2)、 的单调减区间;(3)、 在区间 上值域?20. 湖南株洲市某高科技企业决定开发生产一款大型电子设备.生产这种设备的年固定成本为500万元,每生产 台,需要另投入成本 (万元),当年产量小于60台时, (万元);当年产量不少于60台时 (万元).若每台设备的售价为100万元,通过市场分析,假设该企业生产的电子设备能全部售.(1)、求年利润 (万元)关于年产量 (台)的函数关系式?(2)、年产量为多少台时,该企业在这一款电子设备的生产中获利最大?
