湘教版初中数学八年级上学期期末复习专题7 等腰三角形
试卷更新日期：2021-12-15 类型：复习试卷
一、单选题
-
1. 等腰三角形的两条边长分别为8和4，则它的周长等于（ ）A、12 B、16 C、20 D、16或202. 如图，△ABC中，AB=AC ， AD=DE ， ∠BAD＝18°，∠EDC＝12°，则∠DAE的度数是（ ）
A、52° B、58° C、60° D、62°3. 在△ABC中，AB＝BC ， 中线AD将这个三角形的周长分成15和12两部分，则AC的长为（ ）A、7 B、11 C、7或11 D、8或104. 等腰三角形周长为13cm，其中一边长3cm，则该等腰三角形底边长为（ ）A、7cm B、7cm或3cm C、3cm D、8cm5. 一条船从海岛A出发，以15海里/时的速度向正北航行，2小时后到达海岛B处．灯塔C在海岛A的北偏东43°方向上，在海岛B的北偏东86°方向上．则海岛B到灯塔C的距离是（ ）A、15海里 B、20海里 C、30海里 D、60海里6. 如果一等腰三角形的周长为27，且两边的差为12，则这个等腰三角形的腰长为（ ）A、13 B、5 C、5或13 D、17. 下列给出的5个图中，能判定 是等腰三角形的有（ ）
A、2个 B、3个 C、4个 D、5个8. 如图，D是△ABC中BC边上一点，AB＝AC＝BD ， 则∠2＝24°则∠1＝（ ）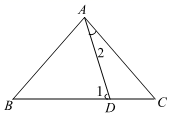
A、44° B、68° C、64° D、54°9. 如图，已知∠MON＝30°，点A1、A2、A3…在射线N上，点B1、B2、B3……在射线OM上；△A1B1A2、△A2B2A3、△A3B3A4……均为等边三角形若OA1＝1，则△A2020B2020A2021的边长（ ）
A、22019 B、4040 C、4038 D、2202010. 如图，在△ABC 中，∠ABC 的平分线交 AC 于点 D，AD＝6，过点 D 作 DE∥BC 交 AB 于点 E， 若△AED 的周长为 16，则边 AB 的长为（ ）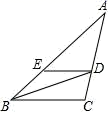
A、6 B、8 C、10 D、1二、填空题
-
11. 用三根木棒首尾相连围成一个等腰三角形，其中两根木棒的长度分别为 和 ，则第三根木棒的长为 ．12. 如图，在△ABC中，点D在边BC上，AB＝AD＝DC ， ∠C＝35°，则∠BAD＝度．
13. 如图，已知△ABC是等边三角形，BC=BD，∠CBD=90°，则∠1的度数是.
14. 如图， 是等边 的 边上的中点，点 在 的延长线上， ， 的周长是9，则 ．
15. 如图，△ABC是等边三角形，∠CBD=90°，BD=BC ， 连接AD交BC于点E ， 则∠AEC的度数是 ．
16. 如图，△ABC中，AB＝8，AC＝6，BC＝5，∠ABC与∠ACB的平分线相交于点O ， 过O点作DE∥BC ， 则△ADE的周长为 ．
三、作图题
-
17. 如图，已知在 中， ， ，请用一直线将这个三角形分成两个等腰三角形.（要求两种不同的分法并写出每个等腰三角形的内角度数）
四、解答题
-
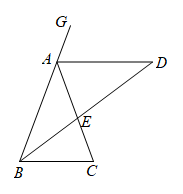
18. 如图，在△ABC 中，∠ABC=60°，∠ACB=82°，延长CB至D ， 使DB=BA ， 延长BC至E ， 使CE=CA ， 连接AD ， AE ． 求∠D ， ∠E ， ∠DAE 的度数．
19. 某地地震过后，河沿村中学的同学用下面的方法检测教室的房梁是否水平；在等腰直角三角尺斜边中点拴一条线绳，线绳的另一端挂一个铅锤，把这块三角尺的斜边贴在房梁上，结果线绳经过三角尺的直角顶点，同学们由此确信房梁是水平的，他们的判断对吗？为什么？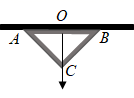
20. 如图，在△ABC中，AB=AC，点E是AC上一点，ED⊥BC于点D，DE的延长线交BA的延长线于点F．求证：△AEF是等腰三角形．
五、综合题
-
21. 如图，在△ABC中，AB＝AC ， 点D、E、F分别在AB、BC、AC边上，且BE＝CF ， BD＝CE ．
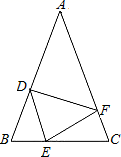(1)、求证：△DEF是等腰三角形；(2)、当∠A＝40°时，求∠DEF的度数．22. 如图： 是等腰三角形，
(1)、若 ，请你将三角形 分成两个等腰三角形，画一画，并标出各角的度数.(2)、若剪一刀，能将分割成两个等腰三角形，则 度数是多少？（直接写出答案）
-
