湘教版初中数学八年级上学期期末复习专题6命题与证明

试卷更新日期：2021-12-14 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列说法中，①三角形的中线、角平分线、高都是线段；②三角形的三条角平分线、三条中线、三条高都在三角形内部；③直角三角形只有一条高；④三角形的三条角平分线、三条中线、三条高分别交于一点．正确的是（）

A、① B、①④ C、②③ D、②④

查看试题解析
2. 用反证法证明“在△ABC中，若∠A＞∠B＞∠C，则∠A＞60°”时，应先假设（）

A、∠A＝60° B、∠A＜60° C、∠A≤60° D、∠A≠60°

查看试题解析
3. 下列语句中不是命题的是（）

A、作直线AB垂直于直线CD B、两直线平行，同位角相等 C、若|a|=|b|，则a²=b² D、同角的补角相等

查看试题解析
4. 对于命题“如果 $∠ 1 + ∠ 2 = 90 °$ ，那么 $∠ 1 \neq ∠ 2$ ”，能说明它是假命题的反例是（）

A、 $∠ 1 = 60 °$ ， $∠ 2 = 40 °$ B、 $∠ 1 = 50 °$ ， $∠ 2 = 40 °$ C、 $∠ 1 = ∠ 2 = 40 °$ D、 $∠ 1 = ∠ 2 = 45 °$

查看试题解析
5. 下列命题的逆命题是假命题的是（）

A、直角三角形的两个锐角互余 B、有两边相等的三角形是等腰三角形 C、相等的两个角是对顶角 D、如果a＞0，b＞0，那么a+b＞0

查看试题解析
6. 下列命题是假命题的是（）．

A、同一平面内，两直线不相交就平行 B、对顶角相等 C、互为邻补角的两角和为180° D、相等的两个角一定是对顶角

查看试题解析
7. 已知△ABC中，AB=AC，求证：∠B＜90°，下面写出运用反证法证明这个命题的四个步骤：
①所以∠A+∠B+∠C＞180°，这与三角形内角和为180°矛盾 ②因此假设不成立.所以∠B＜90°③假设在△ABC中，∠B≥90° ④由AB=AC，得∠C=∠B≥90°，即∠B+∠C≥180°. 这四个步骤正确的顺序应是（）

A、④③①② B、③④②① C、①②③④ D、③④①②

查看试题解析
8. 牛顿曾说：“反证法是数学家最精良的武器之一”.用反证法证明命题“在△ABC中，若AB≠AC，则∠B≠∠C”，首先应假设（）

A、∠B＝∠C B、AB＝AC C、∠B≥∠C D、∠B≤∠C

查看试题解析
9. 用反证法证明命题“在直角三角形中，必有一个锐角不小于45°”时，首先应假设这个直角三角形中（）

A、两个锐角都大于45° B、两个锐角都小于45° C、两个锐角都不大于45° D、两个锐角都等于45°

查看试题解析
10. 用反证法证明“直角三角形中至少有一个锐角不大于45°”，应先假设（）

A、直角三角形中两个锐角都大于45° B、直角三角形中两个锐角都不大于45° C、直角三角形中有一个锐角大于45° D、直角三角形中有一个锐角不大于45°

查看试题解析

二、填空题

11. 写出命题“等腰三角形的两个底角相等”的逆命题：．

查看试题解析
12. 写出命题“全等三角形的周长相等”的逆命题：．

查看试题解析
13. 把命题“如果直角三角形的两直角边长分别为a、b，斜边长为c，那么 $a^{2} + b^{2} = c^{2}$ ”的逆命题改写成“如果……，那么……”的形式：.

查看试题解析
14. 请写出命题“直角三角形的两个锐角互余”的逆命题：．

查看试题解析
15. “直角三角形有两个角是锐角”这个命题的逆命题是，它是一个命题（填“真”或“假”）.

查看试题解析

三、解答题

16. 阅读下列文字，回答问题.
题目：在Rt△ABC中，∠C=90°，若∠A≠45°，所以AC≠BC．

证明：假设AC=BC，∵∠A≠45°，∠C=90°，∴∠A≠∠B，∴AC≠BC．这与假设矛盾，所以AC≠BC．

上面的证明有没有错误？若没有错误，指出其证明的方法；若有错误，请予以纠正.

查看试题解析
17. 写出命题“如果一个角的两边与另一个角的两边分别垂直，那么这两个角相等”的逆命题，并判断原命题和逆命题的真假．若是假命题，请举出反例．

查看试题解析
18. 已知：如图，直线a ， b被c所截，∠1，∠2是同位角，且∠1≠∠2．
求证：a不平行于b ．

查看试题解析

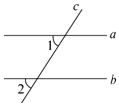
四、综合题

19. 探究问题：已知∠ABC ，画一个角∠DEF ，使DE∥AB ， EF∥BC ，且DE交BC于点P ． ∠ABC与∠DEF有怎样的数量关系？

(1)、我们发现∠ABC与∠DEF有两种位置关系：如图1与图2所示．
①图1中∠ABC与∠DEF数量关系为；图2中∠ABC与∠DEF数量关系为；

请选择其中一种情况说明理由．

②由①得出一个真命题（用文字叙述）：．

(2)、应用②中的真命题，解决以下问题：
若两个角的两边互相平行，且一个角比另一个角的2倍少30°，请直接写出这两个角的度数．

查看试题解析
20. 写出下列命题的逆命题，并判断原命题和逆命题的真假：

(1)、若 $m^{2} \neq n^{2}$ ，则 $m \neq n$ ；

(2)、如果一个三角形有一个内角是钝角，那么它的另外两个内角是锐角。

查看试题解析
21. 探究问题：已知 $∠ A B C$ ，画一个角 $∠ D E F$ ，使 $D E / / A B ， E F / / B C$ ，且 $D E$ 交 $B C$ 于点 $P$ . $∠ A B C$ 与 $∠ D E F$ 有怎样的数量关系？

(1)、我们发现 $∠ A B C$ 与 $∠ D E F$ 有两种位置关系：如图1与图2所示.
①图1中 $∠ A B C$ 与 $∠ D E F$ 数量关系为；图2中 $∠ A B C$ 与 $∠ D E F$ 数量关系为.请选择其中一种情况说明理由.

②由①得出一个真命题（用文字叙述）：.

(2)、应用②中的真命题，解决以下问题：若两个角的两边互相平行，且一个角比另一个角的2倍少30°，请直接写出这两个角的度数.

查看试题解析
22.
如图，有以下3句话：①AB∥CD，②∠B=∠C、③∠E=∠F、请以其中2句话为条件，第三句话为结论构造命题.

(1)、你构造的是哪几个命题？

(2)、你构造的命题是真命题还是假命题？请加以证明.

查看试题解析