浙教版备考2022年中考数学一轮复习专题3 无理数与实数

试卷更新日期：2021-12-14 类型：一轮复习

进入出卷网下载

一、单选题

1. 在实数 $\frac{22}{7} ， 3.14159265 ， \sqrt[3]{9} ， - 8 ， \sqrt[3]{2} ， \sqrt{36} ， \frac{π}{3}$ 中，无理数的个数为（　　）

A、1 B、2 C、3 D、4

查看试题解析
2. $\sqrt{169}$ 的平方根为（　　）

A、13 B、±13 C、 $\sqrt{13}$ D、± $\sqrt{13}$

查看试题解析
3. 已知x为实数，且 $\sqrt[3]{x - 3}$ ﹣ $\sqrt[3]{2 x + 1}$ ＝0，则x²＋x﹣3的算术平方根为（）

A、3 B、2 C、3和﹣3 D、2和﹣2

查看试题解析
4. 的显示结果是（）

A、15 B、±15 C、-15 D、25

查看试题解析
5. 下面说法中，正确的是（）

A、实数分为正实数和负实数 B、带根号的数都是无理数 C、无限不循环小数都是无理数 D、平方根等于本身的数是1和0

查看试题解析
6. 如图，数轴上的点 $A ， B ， C ， D ， E$ 分别对应的数是 $1 ， 2 ， 3 ， 4 ， 5$ ，那么表示 $\sqrt{11} - 1$ 的点应在（）

A、线段 $A B$ 上 B、线段 $B C$ 上 C、线段 $C D$ 上 D、线段 $D E$ 上

查看试题解析
7. 如图，长方形OABC的OA长为2，AB长为1，OA在数轴上，点O与原点重合，以原点为圆心，对角线OB的长为半径画弧，交负半轴于一点，则这个点表示的实数是（）

A、2.5 B、－2 $\sqrt{2}$ C、 $\sqrt{3}$ D、－ $\sqrt{5}$

查看试题解析
8. 有七个数， $0. 4_{}^{•} \overset{•}{2}$ ， $\frac{3}{7}$ ， $\frac{11}{26}$ ，0.424和 $\frac{26}{61}$ 是其中的五个，已知从小到大排列第三个数是 $\frac{11}{26}$ ，那么，从大到小排列的第三个数是（）．

A、 $\frac{11}{26}$ B、 $\frac{3}{7}$ C、 $0. 4_{}^{•} \overset{•}{2}$ D、0.424

查看试题解析
9. 下列各组数中互为相反数的是（）

A、 $5$ 和 $\sqrt{{(- 5)}^{2}}$ B、 $- 5$ 和 $\frac{1}{5}$ C、 $- \sqrt[3]{8}$ 和 $\sqrt[3]{- 8}$ D、 $- | - \sqrt{2} |$ 和 $- (- \sqrt{2})$

查看试题解析
10. 计算： $| 1 + \sqrt{3} | + | \sqrt{3} - 2 |$ ＝（　　）

A、 $2 \sqrt{3} - 1$ B、 $1 - 2 \sqrt{3}$ C、﹣1 D、3

查看试题解析

二、填空题

11. 计算： $2 \sin^{2} 45 ° + \tan 60 ° \cdot \tan 30 ° - \cos 60 ° =$ ．

查看试题解析
12. 若 $\sqrt{7}$ 的整数部分为a，小数部分为b，则b= ，数轴上表示实数a，b的两点之间距离为。

查看试题解析
13. 如图，用两个面积为3cm²的小正方形纸片剪拼成一个大的正方形，则以数轴上表示1的点A为圆心，以大正方形的边长为半径画弧，与数轴的交点表示的实数是．

查看试题解析
14. 如果一个正数的两个平方根是2a＋1和4﹣3a ，那么这个正数是．

查看试题解析
15. 若x³＝64，则 $\sqrt{x}$ ＝．

查看试题解析
16. 已知一个数的两个平方根分别是7和a﹣4，则a＝．

查看试题解析

三、综合题

17. 我们在学习二次根式时，了解了分母有理化及其应用．其实，还有一个类似的方法叫做“分子有理化”，即分母和分子都乘以分子的有理化因式，从而消除分子中的根式．
比如： $\sqrt{7} - \sqrt{6} = \frac{(\sqrt{7} - \sqrt{6}) (\sqrt{7} + \sqrt{6})}{\sqrt{7} + \sqrt{6}}$ ＝ $\frac{1}{\sqrt{7} + \sqrt{6}}$ ．

分子有理化可以用来比较某些二次根式的大小，也可以用来处理一些二次根式的最值问题．例如：比较： $\sqrt{7} - \sqrt{6}$ 和 $\sqrt{6} - \sqrt{5}$ 的大小可以先将它们分子有理化如下： $\sqrt{7} - \sqrt{6} = \frac{1}{\sqrt{7} + \sqrt{6}}$ ， $\sqrt{6} - \sqrt{5} = \frac{1}{\sqrt{6} + \sqrt{5}}$ ．

因为 $\sqrt{7} + \sqrt{6} > \sqrt{6} + \sqrt{5}$ ，所以， $\sqrt{7} - \sqrt{6} < \sqrt{6} - \sqrt{5}$ ．

再例如，求y＝ $\sqrt{x + 2} - \sqrt{x - 2}$ 的最大值、做法如下：

解：由x＋2≥0，x﹣2≥0可知x≥2，而y＝ $\sqrt{x + 2} - \sqrt{x - 2}$ ＝ $\frac{4}{\sqrt{x + 2} + \sqrt{x - 2}}$ ．当x＝2时，分母 $\sqrt{x + 2} + \sqrt{x - 2}$ 有最小值2.所以y的最大值是2

利用上面的方法，完成下面问题：

(1)、比较 $\sqrt{19}$ ﹣ $\sqrt{18}$ 和 $\sqrt{18}$ ﹣ $\sqrt{17}$ 的大小；

(2)、求y＝ $\sqrt{x + 1}$ ﹣ $\sqrt{x - 1}$ ＋2的最大值．

查看试题解析
18. 学习了无理数之后，我们已经把数的领域扩大到了实数的范围，下面让我们在几个具体的图形中认识一下无理数．

(1)、如图1，直径为1个单位长度的圆从原点O沿数轴向右滚动一周，圆上的一点P（开始滚动时与点O重合）由原点到达点O′，则OO′的长度就等于圆的周长，所以数轴上点O′代表的实数就是，它是一个无理数．

(2)、如图2，在Rt△ABC中，∠C＝90°，AC＝2，BC＝1，根据勾股定理可以求得AB＝．

(3)、你能在6×5的网格图中（图3）（每个小正方形边长均为1），画出一条长为 $\sqrt{10}$ 的格点线段吗？如果能，请在图中表示出来．

(4)、请你在数轴上（图4）找到表示 $\sqrt{5}$ 的点．

查看试题解析
19. 已知 $| 2 a + b |$ 与 $\sqrt{3 b + 12}$ 互为相反数．

(1)、求 $6 a - 13 b$ 的平方根和立方根；

(2)、解关于x的方程 $a x^{2} + 4 b - 2 = 0$ ．

查看试题解析
20. 课堂上，老师让同学们从下列数中找一个无理数：
$- \frac{22}{7}$ ， $- \sqrt{2}$ ， $| - \frac{1}{2} |$ ，0， $2 π$ ， $- \sqrt[3]{8}$ ，

其中，甲说“ $- \frac{22}{7}$ ”，乙说“ $- \sqrt{2}$ ”，丙说“ $2 π$ ”

(1)、甲、乙、丙三个人中，说错的是．

(2)、请将老师所给的数字按要求填入下面相应的区域内；

查看试题解析
21. 计算或解方程

(1)、 ${(\frac{1}{2} - \sqrt{3})}^{0}$ ﹣4tan45°+6cos60°﹣|﹣5|

(2)、解方程（x-1)²=3x(x-1）

查看试题解析
22. 如图，纸上有五个边长为1的小正方形组成的图形纸（图1），我们可以把它剪开拼成一个正方形（图2）．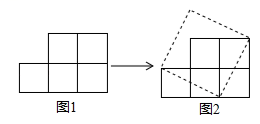

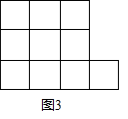(1)、图2中拼成的正方形的面积是；边长是；（填实数）

(2)、你能把十个小正方形组成的图形纸（图3），剪开并拼成正方形吗？若能，请仿照图2的形式把它重新拼成一个正方形．并求出它的边长.

查看试题解析
23. 阅读下面文字，然后回答问题．
给出定义：一个实数的整数部分是不大于这个数的最大数，这个实数的小数部分为这个数与它的整数部分的差的绝对值．例如：2.4的整数部分为2，小数部分为 $2.4 - 2 = 0.4$ ； $\sqrt{2}$ 的整数部分为1，小数部分可用 $\sqrt{2} - 1$ 表示；再如，﹣2.6的整数部分为﹣3，小数部分为 $| - 2.6 - (- 3) | = 0.4$ ．由此我们得到一个真命题：如果 $\sqrt{2} = x + y$ ，其中 $x$ 是整数，且 $0 < y < 1$ ，那么 $x = 1$ ， $y = \sqrt{2} - 1$ ．

(1)、如果 $\sqrt{7} = a + b$ ，其中 $a$ 是整数，且 $0 < b < 1$ ，那么 $a =$ ， $b =$ ；

(2)、如果 $- \sqrt{7} = c + d$ ，其中 $c$ 是整数，且 $0 < d < 1$ ，那么 $c =$ ， $d =$ ；

(3)、已知 $3 + \sqrt{7} = m + n$ ，其中m是整数，且 $0 < n < 1$ ，求 $| m - n |$ 的值；

查看试题解析
24. 如图（1），在4×4的方格中，每个小正方形的边长为1．

(1)、求图（1）中正方形ABCD的面积；

(2)、如图（2），若点A在数轴上表示的数是﹣1，以A为圆心，AD为半径画圆弧与数轴的正半轴交于点E，则点E所表示的数是．

查看试题解析
25. 阅读下面的文字，解答问题：
大家知道 $\sqrt{2}$ 是无理数，而无理数是无限不循环小数，因此 $\sqrt{2}$ 的小数部分我们不可能全部地写出来，于是小明用 $\sqrt{2} - 1$ 来表示 $\sqrt{2}$ 的小数部分，因为 $\sqrt{2}$ 的整数部分是1，将这个数减去其整数部分，差就是小数部分．又例如：∵ $\sqrt{4}$ ＜ $\sqrt{7}$ ＜ $\sqrt{9}$ ，即2＜ $\sqrt{7}$ ＜3，∴ $\sqrt{7}$ 的整数部分为2，小数部分为（ $\sqrt{7}$ ﹣2）．

请解答：

(1)、 $\sqrt{15}$ 的整数部分是，小数部分是；

(2)、已知（ $2 + \sqrt{6}$ ）的小数部分为 $a$ ，（ $5 - \sqrt{6}$ ）的小数部分为 $b$ ，计算 $a + b$ 的值．

查看试题解析
26. 如图1，这是由8个同样大小的立方体组成的魔方，体积为64．

(1)、求出这个魔方的棱长．

(2)、图中阴影部分是一个正方形ABCD，求出阴影部分的面积及其边长．

(3)、把正方形ABCD放到数轴上，如图2，使得A与﹣1重合，那么D在数轴上表示的数为．

查看试题解析
27. 若 $x = \frac{1}{\sqrt{6} - 2}$ ， $y = \frac{1}{\sqrt{6} + 2}$ .

(1)、求 $x^{2} - x y + y^{2}$ 的值；

(2)、若 $x$ 的小数部分为 $m$ ， $y$ 的小数部分为 $n$ ，求 $(m + n) (m - n)$ 的值.

查看试题解析