浙教版备考2022年中考数学一轮复习专题2 代数式、整式、因式分解

试卷更新日期：2021-12-14 类型：一轮复习

进入出卷网下载

一、单选题

1. 多项式x²+4x-3的次数是（）

A、3 B、2 C、1 D、0

查看试题解析
2. 将教材中“整式及整式加减”单元建立如图所示的知识结构图，图中A和B分别表示的是（　　）

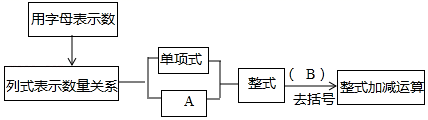A、单项式，因式分解 B、单项式，合并同类项 C、多项式，因式分解 D、多项式，合并同类项

查看试题解析
3. 下列计算正确的是（）

A、8ab-3a=5b B、(-3a²b)²= 6a⁴b² C、(a+1)²=a²+1 D、2a²b÷b=2a²

查看试题解析
4. 已知x^a＝4，x^b＝5，则x^3a﹣2b等于（　　）

A、 $\frac{64}{25}$ B、 $\frac{16}{10}$ C、 $\frac{16}{25}$ D、 $\frac{4}{5}$

查看试题解析
5. 将一组数 $\sqrt{3}$ ， $\sqrt{6}$ ，3， $\sqrt{12}$ ， $\sqrt{15}$ ，……， $\sqrt{228}$ 按下面的方法进行排列：
$\sqrt{3}$ $\sqrt{6}$ 3 $\sqrt{12}$ $\sqrt{15}$

$\sqrt{18}$ $\sqrt{21}$ $\sqrt{24}$ $\sqrt{27}$ $\sqrt{30}$

……

若 $\sqrt{12}$ 的位置记为 $(1 ， 4)$ ， $\sqrt{24}$ 的位置记为 $(2 ， 3)$ ，则这组数中最大的有理数的位置记为（）

A、 $(14 ， 4)$ B、 $(14 ， 5)$ C、 $(15 ， 5)$ D、 $(16 ， 1)$

查看试题解析
6. 阅读理解：设 $\vec{a} = (x_{1} ， y_{1}) ， \vec{b} = (x_{2} ， y_{2})$ ，若 $\vec{a} ⊥ \vec{b}$ ，则 $\vec{a} \cdot \vec{b} = 0$ ，即 $x_{1} \cdot x_{2} + y_{1} \cdot y_{2} = 0$ ，已知 $\vec{a}$ =(-2，x+1)， $\vec{b}$ =(3，x+2)，且 $\vec{a} ⊥ \vec{b}$ ，则x的值为（）

A、2或-2 B、1或-4 C、-1或4 D、1

查看试题解析
7. 下列各式的因式分解中正确的是（）

A、 $- a^{2} + a b - a c = - a (a + b - c)$ B、 $9 x y z - 6 x^{2} y^{2} = 3 x y z (3 - 2 x y)$ C、 $3 a^{2} x - 6 b x + 3 x = 3 x (a^{2} - 2 b)$ D、 $\frac{1}{2} x y^{2} + \frac{1}{2} x^{2} y = \frac{1}{2} x y (x + y)$

查看试题解析
8. 下列各式能用完全平方公式进行因式分解的是（）

A、9x²-6x+1 B、x²+x+1 C、x²+2x-1 D、x²-9

查看试题解析
9. 如果多项式x²﹣5x+c可以用十字相乘法因式分解，那么下列c的取值正确的是（　　）

A、2 B、3 C、4 D、5

查看试题解析
10. 如图，已知∠MON＝30°，点A₁、A₂、A₃…在射线N上，点B₁、B₂、B₃……在射线OM上；△A₁B₁A₂、△A₂B₂A₃、△A₃B₃A₄……均为等边三角形若OA₁＝1，则△A₂₀₂₀B₂₀₂₀A₂₀₂₁的边长（　　）

A、2²⁰¹⁹ B、4040 C、4038 D、2²⁰²⁰

查看试题解析

二、填空题

11. 分式 $\frac{4 m n^{2}}{20 m^{2}}$ 中分子、分母的公因式为.

查看试题解析
12. 4x²-(k-1)x+1能用完全平方公式因式分解，则k的值为

查看试题解析
13. 边长为a ， b的长方形的周长为14，面积为10，则 $a^{3} b + a b^{3} + 2 a^{2} b^{2}$ 的值为．

查看试题解析
14. 一个长方形的面积为12ab²-9a²b，若一边长为3ab，则与这条边相邻的另一条边的长为

查看试题解析
15. 若多项式a²+ka+9是完全平方式，则常数k的值为

查看试题解析
16. 若 $\frac{1}{(2 n - 1) (2 n + 1)}$ = $\frac{a}{2 n - 1}$ + $\frac{b}{2 n + 1}$ ，对任意自然数n都成立，则a= ， b=；
计算：m= $\frac{1}{1 \times 3}$ + $\frac{1}{3 \times 5}$ + $\frac{1}{5 \times 7}$ + …+ $\frac{1}{19 \times 21}$ = ．

查看试题解析

三、综合题

17. 某小区院内有一块长为(3a+b)米，觅为(2a+b)米(a>b)的长方形地，现在物业部门计划将该地的周用进行绿化(如图中阴影邰分)中间部分将修建一长方形景点。

(1)、用含a、b的式子表示绿化的面积；

(2)、求出当a=3，b=2时的绿化面积。

查看试题解析
18.

(1)、[探究]根据图①、图②、图③中所标记的图形的长度，解答下列问题：，
⑴利用图①、图②中图形的面积关系分别写出能解释的乘法公式；

⑵图③是用四个长和宽分别为a、b的全等的长方形拼成的一个正方形(所拼图形无重叠无缝隙)，直接写出式子(a+b)²、(a-b)²、ab之间的等量关系；

(2)、[应用]根据探究(2)中探索的结论，完成下列问题：．
①当a+b= 5，ab=-1时，求a-b的值；

②设A= $\frac{a + 3}{4}$ ，B=a-3，化简：(A+B)²-(A-B)²

查看试题解析
19. 计算与分解因式
计算：

(1)、（2x²y）²•（﹣5xy²）÷（14x⁴y³）

(2)、（x+y﹣m+n）（x﹣y﹣m﹣n）．

(3)、16x⁴﹣1；

(4)、（a﹣b）（5a+2b）+（a+6b）（b﹣a）．

查看试题解析
20. 甲、乙两人各持一张分别写有整式A、B的卡片，已知整式 $C = a^{2} - 2 a - 5$ ，下面是甲、乙两人的对话：
甲：我的卡片上写着整式 $A = a^{2} - 4 a + 10$ ，加上整式C后得到最简整式D；

乙：我用最简整式B加上整式C得到整式 $E = 6 a^{2} - 2 a + 8$ ．

根据以上信息，解答下列问题：

(1)、求整式D和整式B；

(2)、当 $a = - 2$ 时，试判断整式D和整式B的大小，并说明理由．

查看试题解析
21. 小红准备完成题目：计算（x² x+2）（x²﹣x）．她发现第一个因式的一次项系数被墨水遮挡住了．

(1)、她把被遮住的一次项系数猜成3，请你完成计算：（x²+3x+2）（x²﹣x）；

(2)、老师说：“你猜错了，这个题目的正确答案是不含三次项的．”请通过计算说明原题中被遮住的一次项系数是多少？

查看试题解析
22. 下面是小彬同学进行整式化简的过程，请认真阅读并完成相应任务．
$3 x^{2} y + 2 x y - 2 (x y + x^{2} y)$

$= 3 x^{2} y + 2 x y - (2 x y + 2 x^{2} y)$ 第一步

$= 3 x^{2} y + 2 x y - 2 x y + 2 x^{2} y$ 第二步

$= 5 x^{2} y$ 第三步

任务1：填空：

①以上化简步骤中，第一步的依据是．

②以上化简步骤中，第步开始出现下午，这一步错误的原因是．

查看试题解析
23. 阅读材料：我们知道， $4 x - 2 x + x = (4 - 2 + 1) x = 3 x$ ，类似地，我们把 $(a + b)$ 看成一个整体，则 $4 (a + b) - 2 (a + b) + (a + b) = (4 - 2 + 1) (a + b) = 3 (a + b)$ ，“整体思想”是中学教学课题中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛．

(1)、尝试应用：把 ${(a - b)}^{2}$ 看成一个整体，合并 $3 {(a - b)}^{2} - 5 {(a - b)}^{2} + 7 {(a - b)}^{2}$ 的结果是．

(2)、已知 $2 x^{2} - 3 y = 6$ ，求 $- 4 x^{2} + 6 y - 5$ 的值．

(3)、拓展探索：
已知 $a - 2 b = 2$ ， $2 b - c = - 5$ ， $c - d = 9$ ，求 $(2 a - c) + (2 b - 3 d) - (4 b - 3 c)$ 的值．

查看试题解析
24.

(1)、先化简，再求值： $- 2 (x^{2} - 3 y) - [x^{2} - 3 (2 x^{2} - 3 y)]$ ，其中 $x = - 1$ ， $y = - 2$ ．

(2)、已知多项式A，B，其中 $A = x^{2} - 2 x + 1$ ，小马在计算 $A + B$ 时，由于粗心把 $A + B$ 看成 $A - B$ ，求得结果为 $- 3 x^{2} - 2 x - 1$ ，请你帮小马算出 $A + B$ 的符合题意结果．

查看试题解析
25. 因式分解

(1)、 $- 12 x y + x^{2} + 36 y^{2}$

(2)、 $m n (m - n) - m (n - m)$

(3)、 $- 4 x^{3} + 20 x^{2} - 24 x$

查看试题解析
26. 某校“数学社团”活动中，小亮对多项式进行因式分解，m²－mn+2m－2n =(m²－mn)+(2m－2n)=m(m－n)+2(m－n) =(m－n)(m+2)．以上分解因式的方法叫做“分组分解法”，请你在小亮解法的启发下，解决下面问题：

(1)、因式分解a³－3a²－9a+27；

(2)、因式分解x²+4y²－4xy－16；

(3)、已知a ， b ， c是 $△$ ABC的三边，且满足 $a^{2} - a b + c^{2} = 2 a c - b c$ ，判断 $△$ ABC的形状并说明理由．

查看试题解析
27. 探究：
第1个： $2^{2} - 2^{1} = 2 \times 2^{1} - 1 \times 2^{1} = 2^{1}$ ，

第2个： $2^{3} - 2^{2} = 2 \times 2^{2} - 1 \times 2^{2} = 2^{2}$ ，

第3个： $2^{4} - 2^{3} = 2 \times 2^{3} - 1 \times 2^{3} = 2^{3}$ ，

……

(1)、请仔细观察，写出第6个等式；

(2)、请你找规律，写出第n个等式；

(3)、计算： $2^{1} + 2^{2} + 2^{3} + \dots 2^{2019} + 2^{2020} - 2^{2021}$ ．

查看试题解析
28. （探索发现）
先观察下面给出的等式，探究其隐含的规律，然后回答问题： $\frac{1}{1 \times 2} = 1 - \frac{1}{2}$ ； $\frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}$ ； $\frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}$ ； $\dots$

(1)、若 $n$ 为正整数，直接写出结果： $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \dots + \frac{1}{n (n + 1)} =$ ．

(2)、（拓展延伸）
根据上面探索的规律，解决下面的问题：

解关于 $x$ 的分式方程： $\frac{1}{(x - 1) (x - 2)} - \frac{1}{(x - 2) (x - 3)} - \frac{2}{(x - 1) (x - 3)} = \frac{x - 5}{x - 3}$ ．

查看试题解析
29. 图1是一个长方形窗户ABCD ，它是由上下两个长方形（长方形AEFD和长方形EBCF）的小窗户组成，在这两个小窗户上各安装了一个可以朝一个方向水平方向拉伸的遮阳帘，这两个遮阳帘的高度分别是a和2b（即DF＝a ， BE＝2b），且b＞a＞0．当遮阳帘没有拉伸时（如图1），窗户的透光面积就是整个长方形窗户（长方形ABCD）的面积．
如图2，上面窗户的遮阳帘水平方向向左拉伸2a至GH ．当下面窗户的遮阳帘水平方向向右拉伸2b时，恰好与GH在同一直线上（即点G、H、P在同一直线上）．

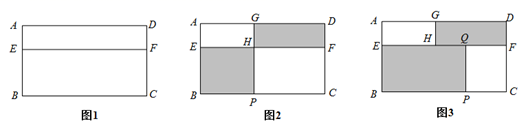(1)、求长方形窗户ABCD的总面积；（用含a、b的代数式表示）

(2)、如图3，如果上面窗户的遮阳帘保持不动，将下面窗户的遮阳帘继续水平方向向右拉伸b至PQ时，求此时窗户透光的面积（即图中空白部分的面积）为多少？（用含a、b的代数式表示）

(3)、如果上面窗户的遮阳帘保持不动，当下面窗户的遮阳帘拉伸至BC的中点处时，请通过计算比较窗户的透光的面积与被遮阳帘遮住的面积的大小．

查看试题解析
30. （问题提出）用n个圆最多能把平面分成几个区域？
（问题探究）为了解决上面的数学问题，我们采取一般问题特殊化的策略，先从最简单情形入手，再逐次递进，最后猜想得出结论．

探究一：如图1，一个圆能把平面分成2个区域．

探究二：用2个圆最多能把平面分成几个区域？

如图2，在探究一的基础上，为了使分成的区域最多，应使新增加的圆与前1个圆有2个交点，将新增加的圆分成2部分，从而增加2个区域，所以，用2个圆最多能把平面分成4个区域．

探究三：用3个圆最多能把平面分成几个区域？

如图3，在探究二的基础上，为了使分成的区域最多，应使新增加的圆与前2个圆分别有2个交点，将新增加的圆分成 $2 \times 2 = 4$ 部分，从而增加4个区域，所以，用3个圆最多能把平面分成8个区域．

(1)、用4个圆最多能把平面分成几个区域？
仿照前面的探究方法，写出解答过程，不需画图．

(2)、（一般结论）用n个圆最多能把平面分成几个区域？
为了使分成的区域最多，应使新增加的圆与前 $(n - 1)$ 个圆分别有2个交点，将新增加的圆分成部分，从而增加个区域，所以，用n个圆最多能把平面分成个区域．（将结果进行化简）

(3)、（结论应用）
①用10个圆最多能把平面分成个区域；

②用个圆最多能把平面分成422个区域．

查看试题解析