2022年浙江省中考专项复习2 代数式及其运算

试卷更新日期：2021-12-14 类型：一轮复习

进入出卷网下载

一、单选题

1. 单项式 $- 8 π a b$ 的系数是（）

A、8 B、-8 C、 $8 π$ D、 $- 8 π$

查看试题解析
2. 下列各组多项式中，没有公因式的是（　　）

A、ax﹣by和by²﹣axy B、3x﹣9xy和6y²﹣2y C、x²﹣y²和x﹣y D、a+b和a²﹣2ab+b²

查看试题解析
3. 用整式表示"x的2倍与y的和的平方”，正确的是（）

A、(2x+y)² B、2x+ y² C、2x²+ y² D、(2x)²+y²

查看试题解析
4. 如果多项式x²﹣5x+c可以用十字相乘法因式分解，那么下列c的取值正确的是（　　）

A、2 B、3 C、4 D、5

查看试题解析
5. 下列关于分式的判断，正确的是（）

A、当 $x = 2$ 时， $\frac{x + 1}{x - 2}$ 的值为零 B、当 $x \neq 3$ 时， $\frac{x - 3}{x}$ 有意义 C、无论x为何值， $\frac{3}{x + 1}$ 不可能得正整数值 D、无论x为何值， $\frac{3}{x^{2} + 1}$ 的值总为正数

查看试题解析
6. 将分式 $\frac{x^{2}}{x + y}$ 中的x、y的值同时扩大3倍，则分式的值（）

A、扩大3倍 B、缩小到原来的 $\frac{1}{3}$ C、保持不变 D、扩大9倍

查看试题解析
7. 把方程 $2 x = x^{2} - 3$ 化为一般形式后二次项系数为1，则一次项系数与常数项的和是（）．

A、5 B、－1 C、1 D、－5

查看试题解析
8. 估计 $\sqrt{15} \times \sqrt{\frac{1}{3}} + \sqrt{4}$ 的运算结果在哪两个整数之间（）

A、1和2 B、2和3 C、3和4 D、4和5

查看试题解析
9. $a$ 、 $b$ 为实数，且 $a b = 1$ ，设 $P = \frac{a}{a + 1} + \frac{b}{b + 1}$ ， $Q = \frac{1}{a + 1} + \frac{1}{b + 1}$ ，则 $P$ 和 $Q$ 的大小关系是（）

A、 $P > Q$ B、 $P < Q$ C、 $P = Q$ D、不能确定

查看试题解析
10. 如图所示的大长方形被分割成4个大小不同的正方形(1)(2)(4)和一个小长方形(5)，有下列结论：
（ 1 ）若已知小正方形(1)和(2)的周长，就能求出大长方形的周长；（2）若已知小正方形(3)的周长，就能求出大长方形的周长；（3）若已知小正方形(4)的周长，就能求出大长方形的周长；(4) 若已知小长方形(5)的周长，就能求出大长方形的周长。其中正确的是（）

A、(1) (2) (4) B、(1) (2) (3) C、(1) (3) D、(2) (3)

查看试题解析

二、填空题

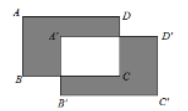
11. 单项式 $\frac{2 π a b^{2}}{5}$ 的次数是．

查看试题解析
12. 因式分解：2a²+4a=.

查看试题解析
13. 将多项式xy²﹣2x²y＋x³﹣1按字母x降幂排列，结果是．

查看试题解析
14. 如果 $\sqrt{\frac{1}{2 x}}$ 有意义，那么实数x的取值范围是．

查看试题解析
15. 若 $3 x^{2} y^{n}$ 与 $- \frac{3}{2} x^{m} y^{3}$ 的差是单项式，则 $m^{n} =$ .

查看试题解析
16. 已知 $x$ 为整数，且 $\frac{2}{x + 3} + \frac{2}{3 - x} + \frac{2 x + 18}{x^{2} - 9}$ 为整数，则所有符合条件的 $x$ 值的和为．

查看试题解析
17. 若|a﹣1|+（ab﹣2）²＝0，则 $\frac{1}{a b} + \frac{1}{(a + 1) (b + 1)}$ $+$ … $+$ $\frac{1}{(a + 10) (b + 10)}$ ＝.

查看试题解析
18. 如图，将长为a cm(a>2)，宽为b cm(b>1)的长方形ABCD先向右平移2cm，再向下平移1cm，得到长方形A'B'C'D'，则阴影部分的面积为cm² ． (用含a、b的代数式表示，结果要求化成最简)

查看试题解析
19. 如果两个多项式有公因式，则称这两个多项式为关联多项式，若x²﹣25与（x＋b）²为关联多项式，则b＝；若（x＋1）（x＋2）与A为关联多项式，且A为一次多项式，当A＋x²﹣6x＋2不含常数项时，则A为.

查看试题解析

三、计算题

20. 化简： $(\frac{x^{2} + x}{x - 1} - x - 1) \div \frac{x^{2} + x}{x^{2} - 2 x + 1}$ .

查看试题解析
21. 计算：（m+n）²﹣（m+n）（m﹣n）+2mn ．

查看试题解析
22. 在实数范围内因式分解：2x²﹣8x+5．

查看试题解析
23. 先化简，再求值：5(3x²y-xy²)-4(-x²y+3xy²)，其中x=-1，y=2，

查看试题解析
24. 化简求值： $\frac{a + 1}{a^{2} - 2 a + 1} \div (2 + \frac{3 - a}{a - 1})$ ，其中 $a = \sqrt{2} + 1$ ．

查看试题解析

四、综合题

25. 一辆出租车从甲地出发，在一条东西走向的街道上行驶，当天行驶的路程记录如下（规定向东为正，x为正整数，单位：千米）： $x ， - \frac{1}{2} x ， x - 6 ， 2 (3 - x)$ ．

(1)、求当天行驶结束后，出租车在甲地的什么位置？

(2)、当 $x = 10$ 时，这辆出租车一共行驶了多少路程？

查看试题解析
26. 如图，阅读下列材料，完成相应的任务：

任务：

(1)、下列四个代数式中，是对称式的是（填序号即可）；
① $a + b + c$ ；② $a^{2} + b^{2}$ ；③ $a^{2} b$ ；④ $\frac{a}{b}$

(2)、写出一个只含有字母 $x ， y$ 的单项式，使该单项式是对称式，且次数为6次；

(3)、已知 $A = 2 a^{2} + 4 b^{2} ， B = a^{2} - 2 a b$ ，求A＋2B ，并直接判断所得结果是否为对称式；

查看试题解析
27. 观察以下等式：① $\frac{1}{1} - \frac{1}{2} = \frac{1}{2} = \frac{1}{1 \times 2}$ ；② $\frac{1}{2} - \frac{1}{3} = \frac{1}{6} = \frac{1}{2 \times 3}$ ；③ $\frac{1}{3} - \frac{1}{4} = \frac{1}{12} = \frac{1}{3 \times 4}$ …，按以上规律解决下列问题：

(1)、第⑤个等式是．

(2)、探究： $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4}$ …+ $\frac{1}{n \times (n + 1)}$ ＝（用含的等式表示）；

(3)、计算：若 $\frac{1}{1 \times 3} + \frac{1}{3 \times 5} + \frac{1}{5 \times 7}$ +… $\frac{1}{(2 n - 1) \times (2 n + 1)}$ ＝ $\frac{16}{33}$ ，求n的值．

查看试题解析
28. 某校“数学社团”活动中，小亮对多项式进行因式分解，m²－mn+2m－2n =(m²－mn)+(2m－2n)=m(m－n)+2(m－n) =(m－n)(m+2)．以上分解因式的方法叫做“分组分解法”，请你在小亮解法的启发下，解决下面问题：

(1)、因式分解a³－3a²－9a+27；

(2)、因式分解x²+4y²－4xy－16；

(3)、已知a ， b ， c是 $△$ ABC的三边，且满足 $a^{2} - a b + c^{2} = 2 a c - b c$ ，判断 $△$ ABC的形状并说明理由．

查看试题解析