2022高考二轮复习选择填空题型 01 集合
试卷更新日期:2021-12-14 类型:二轮复习
一、单选题
-
1. 已知全集 ,集合 , ,那么 ( )A、 B、 C、 D、2. 已知集合 , ,则 元素的个数为A、0 B、1 C、2 D、33. 已知集合 , ,若 ,则实数 的取值范围是( )A、 B、 C、 D、4. 已知集合 ,集合 ,若 ,则 的取值范围为( )A、 B、 C、 D、5. 设集合 ,则 ( )A、 B、 C、 D、6. 已知全集 ,集合 , ,则集合 可能是( )A、{4} B、 C、 D、7. 已知集合A={0,1,3},B={x∈Z|x2-2x+m<0},若A∩B={0,1},则A∪B等于( )A、{0,1,3} B、{0,1,2,3} C、{0,1,2,3,4} D、{-1,0,1,2,3}8. 已知集合 ,集合 ,则集合 的真子集的个数为( )A、3 B、4 C、7 D、89. 已知全集 ,集合 ,集合 ,则阴影部分所示集合为( )
 A、 B、 C、 D、10. 已知 、 ,若 ,则 的值为( )A、-1 B、0 C、1 D、-1或011. 已知函数 ,且 ,函数 的最大值为1,若当 , 时, 的取值范围为 ,则 ( )A、1 B、 C、 D、2
A、 B、 C、 D、10. 已知 、 ,若 ,则 的值为( )A、-1 B、0 C、1 D、-1或011. 已知函数 ,且 ,函数 的最大值为1,若当 , 时, 的取值范围为 ,则 ( )A、1 B、 C、 D、2二、多选题
-
12. 已知集合 ,若集合A有且仅有2个子集,则a的取值有( )A、-2 B、-1 C、0 D、113. 设 表示不大于 的最大整数,已知集合 , ,则( )A、 B、 C、 D、14. 已知全集U的两个非空真子集A,B满足 ,则下列关系一定正确的是( )A、 B、 C、 D、15. 图中阴影部分用集合符号可以表示为( )
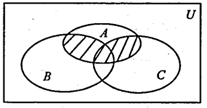 A、 B、 C、 D、16. 已知集合 , ,则下列命题中正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 或 D、若 时,则 或
A、 B、 C、 D、16. 已知集合 , ,则下列命题中正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 或 D、若 时,则 或三、填空题
-
17. 若集合 , , , ,且满足集合 中最大的数大于集合 中最大的数,则称有序集合对 为“兄弟集合对”.当 时,这样的“兄弟集合对”有对;当 时,这样的“兄弟集合对”有对(用含有 的表达式作答).18. 则集合19. 若f(x)= 的定义域为M,g(x)= 的定义域为N,令全集为R,则 =.20. 已知 、 与 、 是4个不同的实数,若关于 的方程 的解集 不是无限集,则集合 中元素的个数构成的集合为.