浙教版备考2022年中考数学一轮复习专题1：实数及其运算

试卷更新日期：2021-12-13 类型：一轮复习

进入出卷网下载

一、单选题

1. 在-1，0.01，π，0，-（-3）， $\frac{22}{7}$ ，这六个数中，正有理数有（）个

A、2个 B、3个 C、4个 D、5个

查看试题解析
2. 若 $- (- 3)$ 表示一个数的相反数，则这个数是（）

A、 $\frac{1}{3}$ B、 $- \frac{1}{3}$ C、 $3$ D、 $- 3$

查看试题解析
3. -7的倒数是（）

A、7 B、 $\frac{1}{7}$ C、 $- \frac{1}{7}$ D、-7

查看试题解析
4. 下列说法错误的是（）

A、开启计算器使之工作的按键是 B、输入－5.8的顺序是 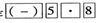C、输入0.58的按键顺序是 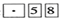D、按键能计算出－69－87的结果

查看试题解析
5. 在有理数 $0$ ， ${(- 1)}^{2}$ ， $- (- \frac{3}{2})$ ， $- | - 2 |$ ， ${(- 2)}^{3}$ 中正数有（）个

A、 $4$ B、 $3$ C、 $2$ D、 $1$

查看试题解析
6. 已知有理数a、b、c在数轴上的对应点的位置如图所示，则下列关系中，正确的是（）

A、 $a + b + c > 0$ B、 $a b c > 0$ C、 $a + b - c > 0$ D、 $0 < \frac{a b}{c} < 1$

查看试题解析
7. 若|a|=3，则a=（）

A、3 B、-3 C、 $\pm 3$ D、 $\pm \frac{1}{3}$

查看试题解析
8. 设a为最小的正整数，b是最大的负整数，c是绝对值最小的数，d是倒数等于自身的有理数，则a－b+c－d的值为（）

A、1 B、－1 C、2或－1 D、1或3

查看试题解析
9. 设n！表示所有小于或等于该数的正整数的积，如4！=1×2×3×4，则计算 $\frac{101 ！ - 100 ！}{99 ！ + 98 ！}$ 的结果为（）

A、100 B、99 C、10 000 D、9 900

查看试题解析
10. 在算式3-|-1□2|中的“□”里，选择一个运算符号，使得算式的值最大（）

A、+ B、- C、× D、÷

查看试题解析

二、填空题

11. 计算：

(1)、 $- {(- 1)}^{5} =$ ；

(2)、 $- 6 + 2 \times (- 1) =$ ．

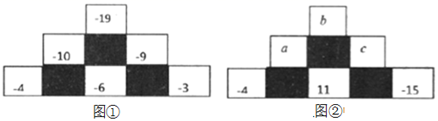
查看试题解析
12. 六三班今天到校47人，请假3人，今天的出勤率是．

查看试题解析
13. 我国第一艘航母“辽宁舰”最大排水虽约为67500吨，若将67500用科学记数法表示为．

查看试题解析
14. 已知(3-m)²+ln+2|=0，则2m+3n的值是

查看试题解析
15. “ $\otimes$ ”定义新运算：对于任意的有理数a和b ，都有 $a \otimes b = b^{2} + 1$ ．例如： $9 \otimes 5 = 5^{2} + 1 = 26$ ．当m为有理数时，则 $m \otimes (m \otimes 3)$ 等于．

查看试题解析
16. 从图①中找出规律，并按规律从图②中找出 $a$ ， $b$ ， $c$ 的值，计算 $a + b - c$ 的值是．

查看试题解析

三、综合题

17. 如图，点A、B、C是数轴上三点，点A、B、C表示的数分别为-10、2、6，我们规定：数铀上两点之间的距离用字母表示．例如：点A与点B之间的距离，可记为AB

(1)、写出AB= ， BC= ，AC=

(2)、点P是A、C之间的点，点P在数轴上对应的数为x
①若PB=5时，则x=

②PA = ， PC= (用含x的式子表示)；

(3)、动点M、N同时从点A、C出发，点M以每秒2个单位长度的速度沿数轴向右运动，点N以每秒2个单位长度的速度沿数向左运动，设运动时间为t(t>0)秒，求当t为何值时，点M、N之间相距2个单位长度？

查看试题解析
18. 规定一种新的运算：a※b=a- 2b，例如：3※2=3-2×2=-1．根据新运算法则，解答下列问题：

(1)、求(-2)※5的值；

(2)、若2※(x+1)=10，求x的值．

查看试题解析
19. 在学习整式加减法时，小明同学做了这样一道题目：
化简：(2x²+ax)-(-2x²+ax+1)

=2x²+ax+2x²-ax-1

=(2+2)x²+(a-a)x-1

=4x²-1

小明发现，化简后含x项的系数和为0，所以整式(2x²+ax)-(-2x²+ax+1)的值和a的取值无关．请根据小明发现的规律，解决下列问题．

已知整式2(ax³+2bx²+1)-4(-x³-3x²+6)的值与a、b的取值无关，回答下列问题：

(1)、直接写出a= ， b=

(2)、求整式2ab²+3a³b的值

(3)、解关于x的方程： $\frac{x + a}{2} - \frac{x + b}{3} = 1$

查看试题解析
20. 观察下列等式：
第一个等式： $2^{2} - 2^{1} = 4 - 2 = 2 = 2^{1}$ ；

第二个等式： $2^{3} - 2^{2} = 8 - 4 = 4 = 2^{2}$ ；

第三个等式： $2^{4} - 2^{3} = 16 - 8 = 8 = 2^{3}$ ；

……

(1)、请按这个顺序仿照前面的等式写出第四个等式；

(2)、根据你上面所发现的规律，用含字母n的式子表示第n个等式；

(3)、请利用上述规律计算： $2^{1} + 2^{2} + 2^{3} + \dots + 2^{2020} + 2^{2021}$ ．

查看试题解析
21. 用数学猜想解决问题
数学猜想即依据已知条件或已有结论，运用实验、观察、归纳、类比的方法，对研究的问题做出由特殊到一般的归纳推测．数学猜想是解决问题的常用方法，也是数学发展的重要思维式．

观察下列等式回答问题：

第一个等式： $\frac{1}{1 \times 2} = 1 - \frac{1}{2}$

第二个等式： $\frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}$

第三个等式： $\frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}$

第四个等式： $\frac{1}{4 \times 5} = \frac{1}{4} - \frac{1}{5}$

(1)、由已知等式可猜想第n个等式为： $\frac{1}{n (n + 1)} =$ ．

(2)、求 $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \dots + \frac{1}{n (n + 1)}$ 的值（要求写出过程，结果用含n的代数式表示）

查看试题解析

22. “十一”黄金周期间，郑州市绿博园在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数，负数表示比前一天少的人数)：

日期

1日

2日

3日

4日

5日

6日

7日

人数变化

单位：万人

+1.6

+0.8

−0.4

−1.4

+0.2

−0.9

(1)、第3天与假期前的游客人数相比，是增加了还是减少了?增加(减少)了多少万人?

(2)、7天假期中平均每天的游客数相较假期前是增加还是减少了?增加(减少)了多少万人?

(3)、请判断7天内游客人数最多的是日.

查看试题解析

23. 蒙阴县的蜜桃闻名全国，现有

20

筐蜜桃，以每筐

23

千克为标准，超过或不足的千克数分别用正数或负数来表示，记录如下：

(1)、与标准重量比较，

20

筐蜜桃总计超过或不足多少千克？

与标准质量的差值

（单位：千克）

$- 3$

$- 2$

$- 1.5$

$0$

$1$

$2.5$

筐数

$1$

$4$

$2$

$3$

$2$

$8$

(2)、若蜜桃每千克售价

5

元，则这

20

筐可卖多少元？

查看试题解析

24. 有理数a，b在数轴上的对应点位置如图所示，且|a|=|c|．

(1)、用“＜”连接这四个数：0，a，b，c；

(2)、化简：|a+b|﹣2|a|﹣|b+c|．

查看试题解析

25. 某工厂本星期内计划每日生产300个机器零件，由于工人实行轮休，每日上班人数不一定相等，实际每日生产量与计划量相比情况如下表（增加的零件数为正数，减少的零件数为负数）：

星期	一	二	三	四	五	六	日
增减	$+ 7$	$- 3$	$+ 10$	$- 5$	$+ 4$	$- 25$	$- 9$

(1)、本星期生产零件个数最多的是星期几？生产了多少个零件？

(2)、本星期总生产量与计划生产量相比，是增加还是减少？增加或减少多少？

(3)、生产零件个数最多的一天比生产零件个数最少的一天多生产了多少个？

查看试题解析

26. 某登山队5名队员以大本营为基地，向海拔距离大本营500米的顶峰发起登顶冲击，假设向上走为正，向下走为负，行程记录如下（单位：米）＋120，－30，－45，＋205，－30，＋25，－20，－5，＋30，＋105，－25，＋90．

(1)、他们有没有登上顶峰？如果没有登上顶峰，他们距离顶峰多少米？

(2)、登山时，5名队员在进行中全程均使用了氧气，每人每100米消耗氧气0.5升，求共使用了多少升氧气？

查看试题解析
27. 已知点A在数轴上对应的数为 $a$ ，点B在数轴上对应的数为 $b$ ，且 $| a + 3 | + | b - 2 | = 0$ ，A、B之间的距离记为 $| A B | = | a - b |$ 或 $| b - a |$ ，请回答问题：

(1)、直接写出 $a$ ， $b$ ， $| A B |$ 的值， $a =$ ， $b =$ ， $| A B | =$ ．

(2)、设点P在数轴上对应的数为 $x$ ，若 $| x - 3 | = 5$ ，则 $x =$ ．

(3)、如图，点M，N，P是数轴上的三点，点M表示的数为 $4$ ，点N表示的数为 $- 1$ ，动点P表示的数为 $x$ ．

①若点P在点M，N之间，则 $| x + 1 | + | x - 4 | =$ _▲_；

②若 $| x + 1 | + | x - 4 | =$ 10，则x=_▲_；

③若点P代表的数是-5，现在有一蚂蚁从点P出发，以每秒1个单位长度的速度向右运动，当经过多少秒时，蚂蚁所经过的点到点M，N的距离之和是8？

查看试题解析
28. 如图，点A、B、C是数轴上三点，点C表示的数为6，BC=4，AB=12．

(1)、写出数轴上点A、B表示的数：，．

(2)、动点P ， Q同时从A ， C出发，点P以每秒4个单位长度的速度沿数轴向右匀速运动，点Q以2个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t>0）秒．
①求数轴上P ， Q表示的数（用含t的式子表示）；

②t为何值时，点P ， Q相距6个单位长度．

查看试题解析
29. 已知下列各有理数：a，b，c的大小关系为 $a < - 1 < b < 0 < 1 < c$ ．

(1)、画出数轴，在数轴上标出这些数表示的点；

(2)、在横线上填上合适的符号（>或<或=）：
① $a + c$ $b + c$ ； ② $a - c$ $a - b$ ；

③ $a b$ $a c$ ； ④ $\frac{a}{b}$ $\frac{a}{c}$ ；

(3)、化简： $| a + b | - | b - c | - | 1 - c |$ ．

查看试题解析
30. 我们知道：在研究和解决数学问题时，当问题所给对象不能进行统一研究时，我们就需要根据数学对象的本质属性的相同点和不同点，将对象区分为不同种类，然后逐类进行研究和解决，最后综合各类结果得到整个问题的解决，这一思想方法，我们称之为“分类讨论的思想”这一数学思想用处非常广泛，我们经常用这种方法解决问题．例如：我们在讨论|a|的值时，就会对a进行分类讨论，当a≥0时，|a|＝a；当a＜0时，|a|＝﹣a ．现在请你利用这一思想解决下列问题：

(1)、 $\frac{8}{| 8 |} =$ ； $\frac{- 3}{| - 3 |} =$ ；

(2)、 $\frac{a}{| a |} =$ （a≠0）， $\frac{a}{| a |} + \frac{b}{| b |} =$ （其中a＞0，b≠0）；

(3)、若abc≠0，试求 $\frac{a}{| a |} + \frac{b}{| b |} + \frac{c}{| c |} + \frac{a b c}{| a b c |}$ 的所有可能的值．

查看试题解析