上海市杨浦区2022届高三上学期数学期中考试试卷

试卷更新日期：2021-12-13 类型：期中考试

进入出卷网下载

一、填空题

1. 函数 $f (x) = x^{- \frac{1}{2}}$ 的定义域为.

查看试题解析
2. 已知集合 $A = {- 1, 2 m - 1}$ ， $B = {m^{2}}$ ，若 $B \subseteq A$ ，则实数 $m =$ ．

查看试题解析
3. ${(1 + 2 x)}^{5} = a_{0} + a_{1} x + a_{2} x^{2} + a_{3} x^{3} + a_{4} x^{4} + a_{5} x^{5}$ ，则 $a_{3} =$ .

查看试题解析
4. 如图，若正四棱柱 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的底面边长为3，高为4，则直线 $B_{1} D$ 与平面 $A B C D$ 所成角的正切值为.

查看试题解析
5. 方程 $\lg (x + 2) = 2 \lg x$ 的解为.

查看试题解析
6. 若 $\arccos x > \frac{π}{3}$ ，则 $x$ 的取值范围为.

查看试题解析
7. 若函数 $f (x) = \sqrt{2 x + 1}$ 的反函数为 $g (x)$ ，则函数 $g (x)$ 的零点为.

查看试题解析
8. 已知函数 $y = \sin (ω x - \frac{π}{6}) (ω > 0)$ 图像的一条对称轴为 $x = \frac{π}{6}$ ，则 $ω$ 的最小值为.

查看试题解析
9. 已知圆锥的底面半径为1，其侧面展开图为一个半圆，则该圆锥的母线长为.

查看试题解析
10. 7人排成一行，甲､乙相邻且丙不排两端的排法有种（用数字作答）

查看试题解析
11. 设 $f (x)$ 是定义在 $R$ 上的函数，且满足 $f (1) = 0$ .若 $y = f (x) + a \cdot 2^{x}$ 是奇函数， $y = f (x) + 3^{x}$ 是偶函数，则 $a$ 的值为.

查看试题解析
12. 在 $△ A B C$ 中， $b = 2$ ， $c = 1$ ， $∠ B - ∠ C = \frac{π}{2}$ ，则 $△ A B C$ 的周长为.

查看试题解析

二、单选题

13. 下列是“ $a > b$ ”的充分不必要条件的是（）

A、 $a > b + 1$ B、 $\frac{a}{b} > 1$ C、 $a^{2} > b^{2}$ D、 $a^{3} > b^{3}$

查看试题解析
14. 下列函数中，既是奇函数，又是减函数的是（）

A、 $y = x^{- 1}$ B、 $y = - \arcsin x$ C、 $y = \log_{2} x$ D、 $y = 2^{x}$

查看试题解析
15. 已知 $f (x) = \sin x$ ，对任意 $x_{1} \in [0 ， \frac{π}{2}]$ ，都存在 $x_{2} \in [0 ， \frac{π}{2}]$ 使得 $f (x_{1}) - 2 f (x_{2} + θ) = - 1$ 成立，则下列 $θ$ 取值可能的是（）

A、 $\frac{3 π}{13}$ B、 $\frac{5 π}{13}$ C、 $\frac{7 π}{13}$ D、 $\frac{9 π}{13}$

查看试题解析
16. 非空集合 $A \subseteq R$ ，且满足如下性质：性质一：若 $a$ ， $b \in A$ ，则 $a + b \in A$ ；性质二：若 $a \in A$ ，则 $- a \in A$ .则称集合 $A$ 为一个“群”以下叙述正确的个数为（）
①若 $A$ 为一个“群”，则 $A$ 必为无限集；②若 $A$ 为一个“群”，且 $a$ ， $b \in A$ ，则 $a - b \in A$ ；③若 $A$ ， $B$ 都是“群”，则 $A \cap B$ 必定是“群”；④若 $A$ ， $B$ 都是“群”，且 $A \cup B \neq A$ ， $A \cup B \neq B$ ，则 $A \cup B$ 必定不是“群”；

A、1 B、2 C、3 D、4

查看试题解析

三、解答题

17. 如图，在正三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A A_{1} = 2$ ， $A B = 3$ ，点 $D$ 为 $B C$ 的中点.

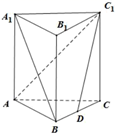(1)、求证：直线 $A_{1} B$ 与 $C_{1} D$ 为异面直线；

(2)、求三棱锥 $B - A C_{1} D$ 的体积.

查看试题解析
18. 已知代数式 ${(\frac{2}{m} + \frac{m}{x})}^{n} (m > 0 ， x > 0)$ .

(1)、当 $m = 2$ ， $n = 6$ 时，求二项展开式中二项式系数最大的项；

(2)、若 ${(\frac{2}{m} + \frac{m}{x})}^{10} = a_{0} + \frac{a_{1}}{x} + \frac{a_{2}}{x^{2}} + \dots + \frac{a_{10}}{x^{10}}$ ，且 $a_{2} = 180$ ，求 $a_{i} (0 \leq i \leq 10 ， i \in N)$ 的最大值.

查看试题解析
19. 为实现“碳达峰”，减少污染，某化工企业开发了一个废料回收项目､经测算，该项目回收成本 $p$ （元）与日回收量 $x$ （吨）（ $x \in [0 ， 50]$ ）的函数关系可表示为 $p = {\begin{array}{l} 20 x ， 0 \leq x \leq 30 \\ x^{2} + 16 x - 780 ， 30 < x \leq 50 \end{array}$ ，且每回收1吨废料，转化成其他产品可收入80元.

(1)、设日纯收益为 $y$ 元，写出函数 $y = f (x)$ 的解析式；（纯收益=收入-成本）

(2)、该公司每日回收废料多少吨时，获得纯收益最大？

查看试题解析
20. 已知函数 $f (x) = 2^{x} + \frac{a}{2^{x}}$ ， $a$ 为实常数.

(1)、若函数 $f (x)$ 为奇函数，求 $a$ 的值；

(2)、若 $x \in [0 ， 1]$ 时 $f (x)$ 的最小值为2，求 $a$ 的值；

(3)、若方程 $f (x) = 6$ 有两个不等的实根 $x_{1}$ ， $x_{2}$ ，且 $| x_{1} - x_{2} | \leq 1$ ，求 $a$ 的取值范围.

查看试题解析
21. 若实数 $x$ ， $y \in [0 ， 2 π]$ ，且满足 $\cos (x + y) = \cos x + \cos y$ ，则称x､y是“余弦相关”的.

(1)、若 $x = \frac{π}{2}$ ，求出所有与之“余弦相关”的实数 $y$ ；

(2)、若实数x､y是“余弦相关”的，求x的取值范围；

(3)、若不相等的两个实数x､y是“余弦相关”的，求证：存在实数z，使得x､z为“余弦相关”的，y､z也为“余弦相关”的.

查看试题解析