江苏省苏州市2021-2022学年高三上学期数学期中考试试卷
试卷更新日期:2021-12-13 类型:期中考试
一、单选题
-
1. 已知集合 ,则 ( )A、 B、 C、 D、2. 若 ,则“ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件3. 若 ,则 ( )A、 B、-7 C、 D、74. 函数 的部分图象大致为( )A、
 B、
B、 C、
C、 D、
D、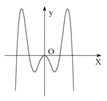 5. 已知 是边长为1的等边三角形,点D,E分别是边 的中点,连结 并延长到点F,使得 ,则 的值为( )A、 B、 C、1 D、-86. 定义方程 的实数根 叫做函数 的“躺平点”.若函数 , 的“躺平点”分别为 , ,则 , 的大小关系为( )A、 B、 C、 D、7. 已知函数 ,直线 与 的图象在 轴右侧交点的横坐标依次为 、 、 、 、 、 ,(其中 ),若 ,则 ( )A、 B、2 C、 D、8. 设数列 ,若存在公比为q的等比数列 ,使得 ,其中 ,则称数列 为数列 的“等比分割数列”,则下列说法错误的是( )A、数列 ;2,4,8,16,32是数列 :3,7,12,24的一个“等比分割数列” B、若数列 存在“等比分割数列” ,则有 和 成立,其中 C、数列 : , ,2存在“等比分割数列” D、数列 的通项公式为 ,若数列 的“等比分割数列” 的首项为1,则公比
5. 已知 是边长为1的等边三角形,点D,E分别是边 的中点,连结 并延长到点F,使得 ,则 的值为( )A、 B、 C、1 D、-86. 定义方程 的实数根 叫做函数 的“躺平点”.若函数 , 的“躺平点”分别为 , ,则 , 的大小关系为( )A、 B、 C、 D、7. 已知函数 ,直线 与 的图象在 轴右侧交点的横坐标依次为 、 、 、 、 、 ,(其中 ),若 ,则 ( )A、 B、2 C、 D、8. 设数列 ,若存在公比为q的等比数列 ,使得 ,其中 ,则称数列 为数列 的“等比分割数列”,则下列说法错误的是( )A、数列 ;2,4,8,16,32是数列 :3,7,12,24的一个“等比分割数列” B、若数列 存在“等比分割数列” ,则有 和 成立,其中 C、数列 : , ,2存在“等比分割数列” D、数列 的通项公式为 ,若数列 的“等比分割数列” 的首项为1,则公比二、多选题
-
9. 已知实数a满足, (i为虚数单位),复数 ,则( )A、z为纯虚数 B、 为虚数 C、 D、10. 已知不等式 的解集是 ,则b的值可能是( )A、-1 B、3 C、2 D、011. 关于函数 有下述四个结论,则( )A、 是偶函数 B、 的最小值为-1 C、 在 上有4个零点 D、 在区间 单调递增12. 如图,正方形 与正方形 边长均为1,平面 与平面 互相垂直,P是 上的一个动点,则( )
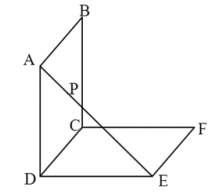 A、 的最小值为 B、当P在直线 上运动时,三棱锥 的体积不变 C、 的最小值为 D、三棱锥 的外接球表面积为
A、 的最小值为 B、当P在直线 上运动时,三棱锥 的体积不变 C、 的最小值为 D、三棱锥 的外接球表面积为三、填空题
-
13. 已知曲线 在 处的切线方程为 ,则 .14. 已知数列 是等差数列, ,则使 的最大整数n的值为.15. 某区域规划建设扇形观景水池,同时紧贴水池周边建设一圈人行步道.要求总预算费用24万元,水池造价为每平方米400元,步道造价为每米1000元(不考虑宽度厚度等因素),则水池面积最大值为平方米.16. 已知 是定义在 上的奇函数,且 ,则 的最小正周期为;若对任意的 ,当时 ,都有 ,则关于x的不等式 在区间 上的解集为.
四、解答题
-
17. 已知向量 ,向量 ,记 .(1)、求 表达式;(2)、解关于x的不等式 .18. 在下列条件:①数列 的任意相邻两项均不相等,且数列 为常数列,② ,③ 中,任选一个,补充在横线上,并回答下面问题.
已知数列 的前n项和为 ,___________.
(1)、求数列 的通项公式 和前n项和 ;(2)、设 ,数列 的前n项和记为 ,证明: .19. 在等腰直角三角形 中,已知 ,点D,E分别在边 , 上, .(1)、若D为 的中点,三角形 的面积为4,求证:E为 的中点;(2)、若 ,求 的面积.
