苏科版数学七年级上册 5.4 主视图、左视图、俯视图 同步训练(1)
试卷更新日期:2021-12-12 类型:同步测试
一、单选题
-
1. 立体图形如图,从上面看到的图形应是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 如图所示的几何体从上面看到的图形是( )
2. 如图所示的几何体从上面看到的图形是( ) A、
A、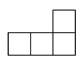 B、
B、 C、
C、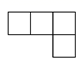 D、
D、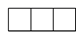 3. 下列几何体中,从正面看到的形状为三角形的是( )A、
3. 下列几何体中,从正面看到的形状为三角形的是( )A、 B、
B、 C、
C、 D、
D、 4. 下列立体图形中,从上面观察你所看到的形状图不是圆的是( )A、
4. 下列立体图形中,从上面观察你所看到的形状图不是圆的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图所示的几何体的从左边看的视图是( )
5. 如图所示的几何体的从左边看的视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 如图的几何体由5个相同的小正方体搭成,从上面看,这个几何体的形状是( )
6. 如图的几何体由5个相同的小正方体搭成,从上面看,这个几何体的形状是( ) A、
A、 B、
B、 C、
C、 D、
D、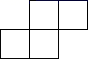 7. 如图,在下面四种用相同的正方体储物箱堆放在一起的形态中,从正面看到的和从左面看到的图形不相同的是( )A、
7. 如图,在下面四种用相同的正方体储物箱堆放在一起的形态中,从正面看到的和从左面看到的图形不相同的是( )A、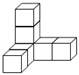 B、
B、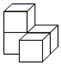 C、
C、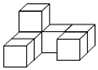 D、
D、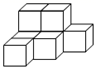 8. 由5个小立方体搭成如图所示的几何体,从正面看到的平面图形是( )
8. 由5个小立方体搭成如图所示的几何体,从正面看到的平面图形是( )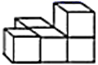 A、
A、 B、
B、 C、
C、 D、
D、 9. 如图是一个由相同小正方体搭成的几何体俯视图,小正方形中的数字表示在该位置上的小正方体的个数,则这个几何题的主视图是 ( )
9. 如图是一个由相同小正方体搭成的几何体俯视图,小正方形中的数字表示在该位置上的小正方体的个数,则这个几何题的主视图是 ( ) A、
A、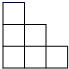 B、
B、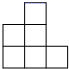 C、
C、 D、
D、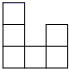 10. 如图是由六个大小相同的小正方体搭成的几何体的俯视图,则该几何体的左视图不可能是( )
10. 如图是由六个大小相同的小正方体搭成的几何体的俯视图,则该几何体的左视图不可能是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 在长方体、圆柱、圆锥、球中,三视图均一样的几何体是12. 下列某种几何体从正面、左面、上面看到的形状图都相同,则这个几何体是(填写序号)①三棱锥;②圆柱;③球.13. 如图,是从不同的方向看一个物体得到的平面图形,该物体的形状是。
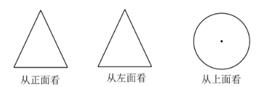 14. 如图是由几个大小相同的小立方块搭成的几何体,搭成这个几何体需要10个小立方块,在保持从正面看和从左面看到的形状图不变的情况下,最多可以拿掉个小立方块.
14. 如图是由几个大小相同的小立方块搭成的几何体,搭成这个几何体需要10个小立方块,在保持从正面看和从左面看到的形状图不变的情况下,最多可以拿掉个小立方块. 15. 一个小立方体的六个面分别标有数字1、2. 3、4、5、6,从三个不同的方向看到的情形如图所示,则数字6的对面是.
15. 一个小立方体的六个面分别标有数字1、2. 3、4、5、6,从三个不同的方向看到的情形如图所示,则数字6的对面是. 16. 如图是由若干个棱长为1的小正方体堆砌而成的几何体,那么这个几何体露在外面的面积是 .
16. 如图是由若干个棱长为1的小正方体堆砌而成的几何体,那么这个几何体露在外面的面积是 .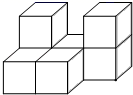 17. 如图是一个几何体的三视图,则这个几何体的侧面积是.(结果保留 ).
17. 如图是一个几何体的三视图,则这个几何体的侧面积是.(结果保留 ).
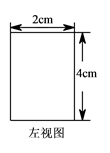
 18. 如图,一个正方体由64块大小相同的小正方体搭成,现从中取走若干个小立方体块,得到一个新的几何体,新几何体与原几何体的三视图(从正面、从左面、从上面看到的所搭几何体的形状图)相同,最多取走块小立方体块.
18. 如图,一个正方体由64块大小相同的小正方体搭成,现从中取走若干个小立方体块,得到一个新的几何体,新几何体与原几何体的三视图(从正面、从左面、从上面看到的所搭几何体的形状图)相同,最多取走块小立方体块.
三、解答题
-
19. 由几个相同的边长为1的小立方块搭成的几何体如图所示,排放在桌面上.
 (1)、请在下面方格纸中分别画出这个几何体从三个不同的方向(上面、正面和左面)看到的视图;(2)、根据三个视图,请你求出这个几何体的表面积(不包括底面积).20.
(1)、请在下面方格纸中分别画出这个几何体从三个不同的方向(上面、正面和左面)看到的视图;(2)、根据三个视图,请你求出这个几何体的表面积(不包括底面积).20.如图所示,观察左图,并在右边的三视图中标出几何体中的相应字母的位置.
 21. 如图,水平放置的长方体的底面是边长为2cm和4cm的矩形,它的左视图的面积为6cm2 , 则长方体的体积是多少?
21. 如图,水平放置的长方体的底面是边长为2cm和4cm的矩形,它的左视图的面积为6cm2 , 则长方体的体积是多少? 22.
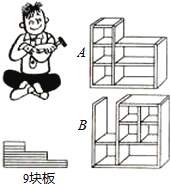
22.王师傅买来九块木板,向自己做一个书架.现在有两个书架的样子,请你观察一下,再猜一猜,王师傅做的是哪个样子的书架,并说明理由.
 23.
23.如图①所示的组合几何体,它的下面是一个长方体,上面是一个圆柱.

(1)图②和图③是它的两个视图,在横线上分别填写两种视图的名称(填“主”、“左”或“俯”);
(2)根据两个视图中的尺寸,计算这个组合几何体的体积.(结果保留π)
24.小明和小彬观察同一个物体,从俯视图看都是一个等腰梯形,但小明所看到的主视图如图(1)所示,小彬看到的主视图如图(2)所示.你知道这是一个什么样的物体?小明和小彬分别是从哪个方向观察它的?
 25.
25.在一个正方体两对侧面各打通一个长方体洞,如图,长方体的一个侧面是正方形,在上面和下面的中心打通一个圆柱体的洞,圆柱直径等于正方形截面的边长.画一画正方体空心部分是一个什么样的几何体.
 26.
26.学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
碟子的个数
碟子的高度(单位:cm)
1
2
2
2+1.5
3
2+3
4
2+4.5
…
…

(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
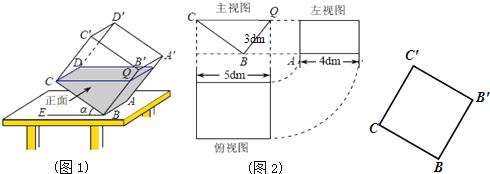
27. 如图所示的几何体是由三个大小完全相同的小正方体组成. (1)、在指定区域内画出从不同的方向看这个几何体得到的平面图形;(2)、已知小正方体的棱长是 ,求这个几何体的体积和表面积.28. 一透明的敞口正方体容器ABCD﹣A′B′C′D′装有一些有色液体,棱AB始终在水平桌面上,容器底部的倾斜角为α (注:图1中∠CBE=α,图2中BQ=3dm).
(1)、在指定区域内画出从不同的方向看这个几何体得到的平面图形;(2)、已知小正方体的棱长是 ,求这个几何体的体积和表面积.28. 一透明的敞口正方体容器ABCD﹣A′B′C′D′装有一些有色液体,棱AB始终在水平桌面上,容器底部的倾斜角为α (注:图1中∠CBE=α,图2中BQ=3dm).探究:如图1,液面刚好过棱CD,并与棱BB′交于点Q,其三视图及尺寸如图2所示,那么:图1中,液体形状为 (填几何体的名称);利用图2中数据,可以算出图1中液体的体积为 dm3 . (提示:V=底面积×高)
拓展:在图1的基础上,以棱AB为轴将容器向左或向右旋转,但不能使液体溢出.若从正面看,若液面与棱C′C或CB交于点P、点Q始终在棱BB′上,设PC=x,请你在下图中把此容器主视图补充完整,并用含x的代数式表示BQ的长度.