苏科版数学七年级上册 5.2 图形的运动 同步训练
试卷更新日期:2021-12-12 类型:同步测试
一、单选题
-
1. 雨滴滴下来形成雨丝属于下列哪个选项的实际应用( )A、点动成线 B、线动成面 C、面动成体 D、以上都不对2. 如图,左面的图形绕虚线旋转一周,可以得到的几何体是
 A、
A、 B、
B、 C、
C、 D、
D、 3. 把如图的三角形绕它的最长边旋转一周,得到的几何体为图中的( )
3. 把如图的三角形绕它的最长边旋转一周,得到的几何体为图中的( )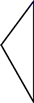 A、
A、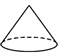 B、
B、 C、
C、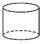 D、
D、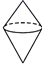 4. 将选项中的直角梯形绕直线旋转一周,可以得到如图的立体图形的是( )
4. 将选项中的直角梯形绕直线旋转一周,可以得到如图的立体图形的是( )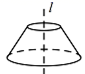 A、
A、 B、
B、 C、
C、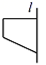 D、
D、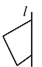 5. 图中的几何体是由哪个图形绕虚线旋转一周得到的( )
5. 图中的几何体是由哪个图形绕虚线旋转一周得到的( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 将图中的三角形绕直线l旋转一周后得到的几何体是( )
6. 将图中的三角形绕直线l旋转一周后得到的几何体是( ) A、
A、 B、
B、 C、
C、 D、
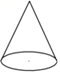
D、 7. 如图,将一个直角三角形绕它的一条直角边所在的直线旋转一周,得到的几何体是圆锥,这一现象能用以下哪个数学知识解释( )
7. 如图,将一个直角三角形绕它的一条直角边所在的直线旋转一周,得到的几何体是圆锥,这一现象能用以下哪个数学知识解释( )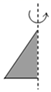
 A、点动成线 B、线动成面 C、面动成体 D、面面相交得线8. 如图所示的几何体是由以下四个图形中的哪一个图形绕着虚线旋转一周得到的( )
A、点动成线 B、线动成面 C、面动成体 D、面面相交得线8. 如图所示的几何体是由以下四个图形中的哪一个图形绕着虚线旋转一周得到的( )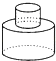 A、
A、 B、
B、 C、
C、 D、
D、 9. 用一平面去截下列几何体,其截面可能是长方形的有( )
9. 用一平面去截下列几何体,其截面可能是长方形的有( )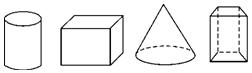 A、1个 B、2个 C、3个 D、4个10. 用一个平面去截一个几何体,若截面的形状是长方形,则原来的几何体不可能是( )A、正方体 B、直棱柱 C、圆柱 D、圆锥
A、1个 B、2个 C、3个 D、4个10. 用一个平面去截一个几何体,若截面的形状是长方形,则原来的几何体不可能是( )A、正方体 B、直棱柱 C、圆柱 D、圆锥二、填空题
-
11. 当笔尖在纸上移动时,形成 , 这说明:;表针旋转时,形成了一个 , 这说明:;长方形纸片绕它的一边旋转,形成的几何图形就是 , 这说明: .12. 下列平面图形中,将编号为(只需填写编号)的平面图形绕轴旋转一周,可得到图中所示的立体图形.
 13. 用一个平面去截一个几何体,截面不可能是圆的几何体的是 .
13. 用一个平面去截一个几何体,截面不可能是圆的几何体的是 .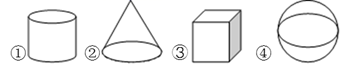 14. 以三角形一直角边为轴旋转一周形成.15. 长方形绕着它的一条边旋转一周后形成的几何体是.16. 长方形的两条边长分别为3cm和4cm,以其中一条边所在的直线为轴旋转一周后得到几何体的底面积是.17. 用平面去截球体与圆柱,如果得到的截面形状相同,那么截面的形状是 .18. 用一个平面去截一个几何体,截面形状为圆,则这个几何体可能为(填序号).
14. 以三角形一直角边为轴旋转一周形成.15. 长方形绕着它的一条边旋转一周后形成的几何体是.16. 长方形的两条边长分别为3cm和4cm,以其中一条边所在的直线为轴旋转一周后得到几何体的底面积是.17. 用平面去截球体与圆柱,如果得到的截面形状相同,那么截面的形状是 .18. 用一个平面去截一个几何体,截面形状为圆,则这个几何体可能为(填序号).①正方体;②圆柱;③圆锥;④正三棱柱
三、解答题
-
19.
图中的立体图形是由哪个平面图形旋转后得到?请用线连起来.
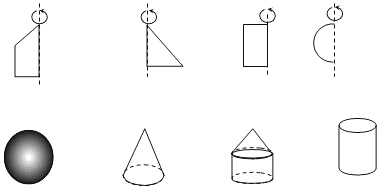 20. 观察图形,回答下列问题:
20. 观察图形,回答下列问题: (1)、图是由几个面组成的,这些面有什么特征?
(1)、图是由几个面组成的,这些面有什么特征?
(2)、图②是由几个面组成的,这些面有什么特征?(3)、图①中共形成了多少条线?这些线都是直的吗?图②呢?(4)、图①和图②中各有几个顶点?21. 小明学习了“面动成体”之后,他用一个边长为3cm、4cm和5cm的直角三角形,绕其中一条边旋转一周,得到了一个几何体.(1)、请画出可能得到的几何体简图.(2)、分别计算出这些几何体的体积.(锥体体积= 底面积×高)22. 已知长方形的长为4cm.宽为3cm,将其绕它的一边所在的直线旋转一周,得到一个几何体,(1)、求此几何体的体积;(2)、求此几何体的表面积.(结果保留π)23.一些立体图形可由一些平面图形绕一条直线旋转而得到,这样的几何体叫旋转体,试思考:
(1)以长方形的一边为轴把长方形绕轴旋转﹣周得到的立体图形是什么?你能画出示意图吗?
(2)把直角三角形以直角边为旋转轴旋转一周得到的几何体又是什么?以斜边呢?你能画出示意图吗?
(3)知果把图绕虚线旋转一周所得的图形是怎样的呢?你能画出示意图吗?
 24.
24.如图,长方形的长和宽分别是7cm和3cm,分别绕着它的长和宽所在的直线旋转一周,回答下列问题:
(1)如图(1),绕着它的宽所在的直线旋转一周,所得到的是什么样的几何体?得到的几何体的体积是多少?(π取3.14)
(2)如图(2),绕着它的长所在的直线旋转一周,所得到的是什么样的几何体?得到的几何体的体积是多少?(π取3.14)
 25. 如图所示,在长方形ABCD中,BC=6cm,CD=8cm.现绕这个长方形的一边所在直线旋转一周得到一个几何体。请解决以下问题:
25. 如图所示,在长方形ABCD中,BC=6cm,CD=8cm.现绕这个长方形的一边所在直线旋转一周得到一个几何体。请解决以下问题: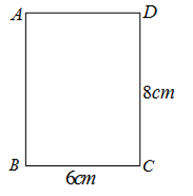 (1)、说出旋转得到的几何体的名称?(2)、如果用一个平面去截旋转得到的几何体,那么截面有哪些形状 至少写出 种 ?(3)、求以CD边所在直线进行旋转所得几何体的体积? 结果保留26. 已知长方形的长为5cm , 宽为4cm , 将其绕它的一边所在的直线旋转一周,得到一个立体图形.
(1)、说出旋转得到的几何体的名称?(2)、如果用一个平面去截旋转得到的几何体,那么截面有哪些形状 至少写出 种 ?(3)、求以CD边所在直线进行旋转所得几何体的体积? 结果保留26. 已知长方形的长为5cm , 宽为4cm , 将其绕它的一边所在的直线旋转一周,得到一个立体图形.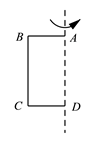 (1)、得到的几何图形的名称为 , 这个现象用数学知识解释为 .(2)、求此几何体的表面积;(结果保留π)(3)、求此几何体的体积.(结果保留π)27. 在直角三角形,两条直角边分别为6cm,8cm,斜边长为10cm,若分别以一边旋转一周(①结果用π表示;②你可能用到其中的一个公式,V圆柱=πr2h,V球体= , V圆锥=h)
(1)、得到的几何图形的名称为 , 这个现象用数学知识解释为 .(2)、求此几何体的表面积;(结果保留π)(3)、求此几何体的体积.(结果保留π)27. 在直角三角形,两条直角边分别为6cm,8cm,斜边长为10cm,若分别以一边旋转一周(①结果用π表示;②你可能用到其中的一个公式,V圆柱=πr2h,V球体= , V圆锥=h)(1)如果绕着它的斜边所在的直线旋转一周形成的几何体是?
(2)如果绕着它的直角边6所在的直线旋转一周形成的几何体的体积是多少?
(3)如果绕着它的斜边10所在的直线旋转一周形成的几何体的体积与绕着直角边8所在的直线旋转一周形成的几何体的体积哪个大?
28. 探究:有一弦长6cm,宽4cm的矩形纸板,现要求以其一组对边中点所在直线为轴,旋转180°,得到一个圆柱,现可按照两种方案进行操作:方案一:以较长的一组对边中点所在直线为轴旋转,如图①;
方案二:以较短的一组对边中点所在直线为轴旋转,如图②.
(1)请通过计算说明哪种方法构造的圆柱体积大;
(2)如果该矩形的长宽分别是5cm和3cm呢?请通过计算说明哪种方法构造的圆柱体积大;
(3)通过以上探究,你发现对于同一个矩形(不包括正方形),以其一组对边中点所在直线为轴旋转得到一个圆柱,怎样操作所得到的圆柱体积大(不必说明原因)?
