初中数学人教版一轮复习专题:专题9 一元一次不等式(组)及其应用
试卷更新日期:2021-12-10 类型:一轮复习
一、单选题
-
1. 已知a<b,则下列不等式中不正确的是( )A、a+4<b+4 B、a﹣4<b﹣4 C、﹣4a<﹣4b D、4a<4b2. 下列说法不一定成立的是( )A、若a>b,则a+c>b+c B、若a+c>b+c,则a>b C、若a>b,则ac2>bc2 D、若ac2>bc2 , 则a>b3. 若a<b<0,则下列式子:①a+1<b+2;② >1;③a+b<ab;④ < 中,正确的有( )A、1个 B、2个 C、3个 D、4个4. 已知a<b<0,x= ,y= ,则下列结论正确的是( )A、x<y B、x>y C、x=y D、无法确定5. 若<2,>-3,则x的取值范围( )
A、 B、 或 C、 或 D、以上答案都不对6. 若不等式 有解,则实数 最小值是( )
A、1 B、2 C、4 D、67. 等式 成立的x的取值范围在数轴上可表示为( )A、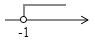 B、
B、 C、
C、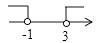 D、
D、 8. 下列是一元一次不等式的有
8. 下列是一元一次不等式的有, , , , , , .
A、1个 B、2个 C、3个 D、4个9. 已知关于x的分式方程 = 的解是非负数,那么a的取值范围是( )A、a>1 B、a≥1 C、a≥1且a≠9 D、a≤110. 某种商品的进价为1200元,标价为1575元,后来由于该商品积压,商店准备打折出售,但要保持利润率不低于5%,则至多可打( )
A、6折 B、7折 C、8折 D、9折11. 若关于 的一元一次不等式组 无解,则 的取值范围是( )A、 ≥1 B、 >1 C、 ≤ D、 <12. 若数a使关于x的不等式组 有且仅有四个整数解,且使关于y的分式方程 + =2有非负数解,则所有满足条件的整数a的值之和是( )
A、3 B、1 C、0 D、﹣3二、填空题
-
13. 如图,数轴上所表示关于 的不等式组的解集是.
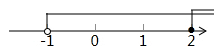 14. 若 ,则 , -b+1,
14. 若 ,则 , -b+1,.(用“
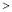 ”,“
”,“ 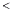 ”或“=”填空)15. 若 是关于 的一元一次不等式,则 .16. 若不等式3x-m≤0的正整数解恰好是1、2、3,则m的取值范围是.
”或“=”填空)15. 若 是关于 的一元一次不等式,则 .16. 若不等式3x-m≤0的正整数解恰好是1、2、3,则m的取值范围是.
17. 若关于 的二元一次方程组 的解都为正整数,则18. 定义新运算:对于任意实数a,b都有:a⊕b=a(a﹣b)+1。如:2⊕5=2×(2﹣5)+1=2×(﹣3)+1=﹣5,那么不等式3⊕x<13的解为。
19. 商家花费760元购进某种水果80千克,销售中有5%的水果正常损耗,为了避免亏本,售价至少应定为元/千克
三、解答题
-
20. 解不等式组: 并把它的解集在数轴上表示出来.并求不等式组的整数解.21. 感知:解不等式 .根据两数相除,同号得正,异号得负,得不等式组 或不等式组 解不等式组 ,得 ;解不等式组 ,得 ,所以原不等式的解集为 或 .(1)、探究:解不等式 .(2)、应用:不等式 的解集是 .22. 今年中考期间,我县部分乡镇学校的九年级考生选择在一中、二中的学生宿舍住宿,某学校将若干间宿舍分配给该校九年级一班的女生住宿,已知该班女生少于25人,若每个房间住4人,则剩下3人没处住;若每个房间住6人,则空一间房,并且还有一间房有人住但住不满。问分配给该校九年级一班女生多少间宿舍,该班有多少名女生?23. 绵阳市“全国文明村”江油白玉村果农王灿收获枇杷20吨,桃子12吨.现计划租用甲、乙两种货车共8辆将这批水果全部运往外地销售,已知一辆甲种货车可装枇杷4吨和桃子1吨,一辆乙种货车可装枇杷和桃子各2吨.(1)、王灿如何安排甲、乙两种货车可一次性地运到销售地有几种方案?(2)、若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费240元,则果农王灿应选择哪种方案,使运输费最少?最少运费是多少?