初中数学人教版一轮复习专题：专题8 分式方程及其应用

试卷更新日期：2021-12-10 类型：一轮复习

进入出卷网下载

一、单选题

1. 下列方程：① $\frac{x - 3}{5}$ =1；② $\frac{3}{x}$ =2；③ $\frac{1 + x}{5 + x}$ $= \frac{1}{2}$ ④ $\frac{x}{2}$ + $\frac{2}{x^{2} + 1}$ =5；⑤ $\frac{x}{π}$ + $\frac{x}{2 π}$ =4.其中是分式方程的是（）

A、①② B、②③ C、③④ D、②③④

查看试题解析
2. 下面说法中，正确的是（）

A、把分式方程化为整式方程，则这个整式方程的解就是这个分式方程的解 B、分式方程中，分母中一定含有未知数 C、分式方程就是含有分母的方程 D、分式方程一定有解

查看试题解析
3. 下列说法：①解分式方程一定会产生增根；②方程 $1 - \frac{4}{x + 2} = 0$ 的根为2；③方程 $\frac{1}{2 x} = \frac{1}{2 x - 4}$ 的最简公分母为 $2 x (2 x - 4)$ ；④ $x + \frac{1}{x - 1} = 1 + \frac{1}{x}$ 是分式方程.其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
4. 用换元法解方程x²-2x+ $\frac{7}{x^{2} - 2 x}$ =8，若设x²-2x=y,则原方程化为关于y的整式方程是( )

A、y²+8y-7=0 B、y²-8y-7=0 C、y²+8y+7=0 D、
y²-8y+7=0

查看试题解析
5. 分式方程 $\frac{x}{x - 1} - 1 = \frac{3}{(x - 1) (x + 2)}$ 的解为（）

A、 $x = 1$ B、 $x = 2$ C、 $x = - 1$ D、无解

查看试题解析
6. 已知 $\frac{3 x + 4}{x^{2} -x- 2}$ = $\frac{A}{x- 2}$ - $\frac{B}{x + 1}$ ，其中A，B为常数，则4A-B的值为（）

A、13 B、9 C、7 D、5

查看试题解析
7. 关于x的方程 $\frac{3 x - 2}{x + 1}$ =2+ $\frac{m}{x + 1}$ 无解，则m的值为（）

A、-5 B、-8 C、-2 D、5

查看试题解析
8. 已知方程 $\frac{k - 1}{x^{2} - 1} - \frac{1}{x^{2} - x} = \frac{k - 5}{x^{2} + x}$ 有增根x=1，那么k的值为（）

A、1 B、 $- 1$ C、3 D、 $- 3$

查看试题解析
9. 从－3，－1， $\frac{1}{2}$ ，1，3这五个数中，随机抽取一个数记为a，若数a使关于x的方程 $(1 - 2 a) x^{2} - 2 x - 1 = 0$ 有实数解，且使关于x的分式方程 $\frac{a x}{x - 3} + \frac{1}{3 - x} = 1$ 有整数解，那么这5个数中所有满足条件的a值之和是（）.

A、﹣3 B、 $- \frac{1}{2}$ C、 $- \frac{3}{2}$ D、 $2$

查看试题解析
10. 若 $\frac{1}{x}$ + $\frac{1}{y}$ = $\frac{1}{x + y}$ ，则 $\frac{y}{x}$ + $\frac{x}{y}$ 的值为（）

A、0 B、1 C、﹣1 D、无法计算

查看试题解析
11. 新能源汽车环保节能，越来越受到消费者的喜爱．各种品牌相继投放市场．一汽贸公司经销某品牌新能源汽车．去年销售总额为5000万元，今年1～5月份，每辆车的销售价格比去年降低1万元．销售数量与去年一整年的相同．销售总额比去年一整年的少20%，今年1﹣5月份每辆车的销售价格是多少万元？设今年1﹣5月份每辆车的销售价格为x万元．根据题意，列方程正确的是（）

A、 $\frac{5000}{x + 1}$ = $\frac{5000 (1 - 20 %)}{x}$ B、 $\frac{5000}{x + 1}$ = $\frac{5000 (1 + 20 %)}{x}$ C、 $\frac{5000}{x - 1}$ = $\frac{5000 (1 - 20 %)}{x}$ D、 $\frac{5000}{x - 1}$ = $\frac{5000 (1 + 20 %)}{x}$

查看试题解析
12. 一艘轮船在静水中的最大航速为30千米/时，它沿江以最大航速顺流航行100千米所用时间，与以最大航速逆流航行60千米所用时间相等，江水的流速为多少？设江水的流速为 $x$ 千米/时，则可列方程（）

A、 $\frac{100}{30 + x} = \frac{60}{30 - x}$ B、 $\frac{100}{x + 30} = \frac{60}{x - 30}$ C、 $\frac{100}{30 - x} = \frac{60}{30 + x}$ D、 $\frac{100}{x - 30} = \frac{60}{x + 30}$

查看试题解析

二、填空题

13. 若 $\frac{m - 3}{m - 1}$ •|m|= $\frac{m - 3}{m - 1}$ ，则m= ．

查看试题解析
14. 如图是一个运算程序的示意图，若输出y的值为2，则输入x的值可能为．

查看试题解析
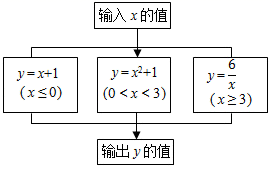15. 已知关于x的分式方程 $\frac{x}{x - 3}$ －2= $\frac{k}{x - 3}$ 有一个正数解，则k的取值范围为.

查看试题解析
16. 已知a>b>0，且 $\frac{2}{a} + \frac{1}{b} + \frac{3}{b-a} = 0$ ，则 $\frac{b}{a} =$ 。

查看试题解析
17. 某服装厂准备加工400套运动装，在加工完160套后，采用了新技术，使得工作效率比原计划提高了20%，结果共用了18天完成任务，问计划每天加工服装多少套？在这个问题中，设计划每天加工x套，则根据题意可得方程为。

查看试题解析
18. 如图，甲，乙两人分别从A、B两地同时出发去往C地，在距离C地2500米处甲追上乙；若乙提前10分钟出发，则在距离C地1000米处甲追上乙。已知，乙每分钟走60米，那么甲的速度是每分钟米。

查看试题解析
19. 观察下列等式：
$\frac{1}{1 \times 2} = 1 - \frac{1}{2}$ ， $\frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}$ ， $\frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}$

将以上三个等式两边分别相加得： $\frac{1}{1 \times 2} +$ $\frac{1}{2 \times 3} +$ $\frac{1}{3 \times 4}$ = $1 - \frac{1}{2}$ + $\frac{1}{2} - \frac{1}{3}$ + $\frac{1}{3} - \frac{1}{4}$ = $1 - \frac{1}{4}$ = $\frac{3}{4}$

猜想并得出： $\frac{1}{n (n + 1)}$ = $\frac{1}{n} - \frac{1}{n + 1}$

根据以上推理，求出分式方程 $\frac{1}{x - 2} + \frac{1}{(x - 2) (x - 3)} + \frac{1}{(x - 3) (x - 4)} = 1$ 的解是．

查看试题解析

三、计算题

20. 解方程： $1 - \frac{1}{x^{2} + 7 x + 6} = \frac{x^{2} - 5 x + 5}{x^{2} - 5 x + 6}$

查看试题解析
21. 解分式方程： $\frac{7}{x^{2} + x} - \frac{3}{x - x^{2}} = 1 + \frac{7 - x^{2}}{x^{2} - 1}$

查看试题解析

四、综合题

22. 已知关于x的分式方程 $\frac{2}{x - 2}$ + $\frac{m x}{x^{2} - 4}$ = $\frac{2}{x + 2}$ .

(1)、若方程的增根为x=2,求m的值;

(2)、若方程有增根,求m的值;

(3)、若方程无解,求m的值.

查看试题解析
23. 某校利用暑假进行田径场的改造维修，项目承包单位派遣一号施工队进场施工，计划用40天时间完成整个工程：当一号施工队工作5天后，承包单位接到通知，有一大型活动要在该田径场举行，要求比原计划提前14天完成整个工程，于是承包单位派遣二号与一号施工队共同完成剩余工程，结果按通知要求如期完成整个工程.

(1)、若二号施工队单独施工，完成整个工程需要多少天？

(2)、若此项工程一号、二号施工队同时进场施工，完成整个工程需要多少天？

查看试题解析
24. 李老师家距学校1900米，某天他步行去上班，走到路程的一半时发现忘带手机，此时离上班时间还有23分钟，于是他立刻步行回家取手机，随后骑电瓶车返回学校．已知李老师骑电瓶车到学校比他步行到学校少用20分钟，且骑电瓶车的平均速度是步行速度的5倍，李老师到家开门、取手机、启动电瓶车等共用4分钟.

(1)、求李老师步行的平均速度；

(2)、请你判断李老师能否按时上班，并说明理由.

查看试题解析