湘教版初中数学九年级上学期期末复习专题14 解直角三角形

试卷更新日期：2021-12-10 类型：复习试卷

进入出卷网下载

一、单选题

1. 已知 $△ A B C$ ，AB＝m ， ∠ACB＝90°，则下列各式中，正确的是（）

A、 $B C = m \cdot \tan A$ B、 $B C = m \cdot \cot A$ C、 $B C = m \cdot \cos A$ D、 $B C = m \cdot \sin A$

查看试题解析
2. 如图，河坝横断面迎水坡 $A B$ 的坡比为 $1： \sqrt{3}$ ．坝高 $B C$ 为 $4 m$ ，则 $A B$ 的长度为（）

A、 $4 \sqrt{3} m$ B、 $8 m$ C、 $8 \sqrt{3} m$ D、 $16 m$

查看试题解析
3. 在Rt $△$ ABC中，∠C＝90°，sinA $= \frac{1}{3}$ ，BC＝2，则AB等于（）

A、 $\frac{2}{3}$ B、4 C、4 $\sqrt{2}$ D、6

查看试题解析
4. 如图要测量小河两岸相对的两点P、A的距离，可以在小河边取 $P A$ 的垂线 $P B$ 上的一点C ，测得 $P C = 50$ 米， $∠ P C A = 44 °$ ，则小河宽 $P A$ 为（）米

A、 $50 \sin 44 °$ B、 $50 \cos 44 °$ C、 $50 \tan 44 °$ D、 $50 \tan 46 °$

查看试题解析
5. 在 $△ A B C$ 中， $∠ C = 90 °$ ， $B C = 2$ ， $\sin A = \frac{2}{3}$ ，则 $A C$ 的长是（）

A、 $\sqrt{5}$ B、3 C、 $\frac{4}{5}$ D、 $\sqrt{13}$

查看试题解析
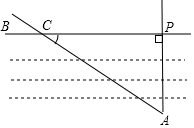6. 某课外数学兴趣小组的同学进行关于测量楼房高度的综合实践活动．如图，他们在距离楼房35米的 $C$ 处测得楼顶的仰角为 $α$ ，则楼房 $A B$ 的高为（）

A、 $35 \sin α$ 米 B、 $35 \tan α$ 米 C、 $\frac{35}{\tan α}$ 米 D、 $\frac{35}{\sin α}$ 米

查看试题解析
7. 如图，在 $△ A B C$ 中， $∠ B = 45 °$ ， $∠ C = 30 °$ ，过点A作 $A C$ 的垂线交 $B C$ 于点D ， $D E$ 平分 $∠ A D C$ 交 $A C$ 于点E ．若 $A E = 2$ ，则 $A B$ 的长为（）

A、 $\sqrt{6}$ B、 $3 \sqrt{2}$ C、 $\frac{3 \sqrt{6}}{2}$ D、3

查看试题解析
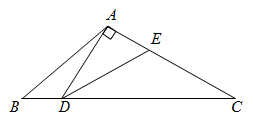8. 如图，小明在学校门口的点C处测得树的顶端A仰角为α，同时测得 $A C = 15 m$ ，则树的高度 $A B$ 为（）

A、 $\frac{15}{\tan α} m$ B、 $15 \tan α m$ C、 $\frac{15}{\sin α} m$ D、 $15 \sin α m$

查看试题解析
9. 定义：在 $∠ C = 30 °$ 的 $△ A B C$ 中，我们把 $∠ A$ 的对边与 $∠ C$ 的对边的比叫做 $∠ A$ 的邻弦，记作 $thi A$ ，即 $thi A = \frac{B C}{A B}$ ．则 $thi 45 °$ 的值为（）．

A、 $\frac{\sqrt{2}}{2}$ B、1 C、 $\sqrt{2}$ D、 $\sqrt{3}$

查看试题解析
10. 如图，已知矩形 $A O B C$ 的三个顶点的坐标分别为 $O (0 ， 0)$ ， $A (0 ， 3 \sqrt{3})$ ， $B (3 ， 0)$ ，按以下步骤作图：①以点 $O$ 为圆心，适当长度为半径作弧，分别交 $O C$ ， $O B$ 于点 $D$ ， $E$ ；②分别以点 $D$ ， $E$ 为圆心，大于 $\frac{1}{2} D E$ 的长为半径作弧，两弧在 $∠ B O C$ 内交于点 $F$ ；③作射线 $O F$ ，交边 $B C$ 于点 $G$ ，则点 $G$ 的坐标为（）

A、 $(3 ， \frac{3 \sqrt{3}}{2})$ B、 $(\frac{3 \sqrt{3}}{2} ， 3)$ C、 $(\sqrt{3} ， 3)$ D、 $(3 ， \sqrt{3})$

查看试题解析

二、填空题

11. 如图，在△ABC中，∠A＝30°，∠B＝45°，AC＝2 $\sqrt{3}$ ，则AB的长为．

查看试题解析
12. 已知在直角三角形ABC中，∠C为直角，tan∠ABC＝2，AC＝2，则AB＝．

查看试题解析
13. 在△ABC中，AB＝5，tan∠ABC＝ $\frac{1}{2}$ ，AC＝ $\sqrt{10}$ ，则BC＝．

查看试题解析
14. 如图所示，四边形ABCD中，∠B＝90°，AB＝2，CD＝8，AC⊥CD，若sin∠ACB＝ $\frac{1}{3}$ ，则cos∠ADC＝．

查看试题解析
15. 寒假在家学习网课时，小李将笔记本电脑水平放置在桌子上，显示屏OB与底板OA所在水平线的夹角为120°，此时感觉最舒适（如图1），侧面示意图为图2.使用时为了散热，他在底板下垫入散热架ACO′后，使电脑变化至AD′位置（如图3），侧面示意图为图4.已知OA＝OB＝24cm，O′C⊥OA于点C，O′C＝12cm.

(1)、∠CAO′＝；

(2)、显示屏的顶部B比原来升高了cm.

查看试题解析
16. 有一种双层长方体垃圾桶AB＝70cm，BC＝25cm，CF＝30cm，侧面如图1所示，隔板EG等分上下两层，下方内桶BCHG绕底部轴（CF）旋转开，若点H恰好能卡在原来点G的位置，则内桶边CH的长度应设计为；现将CH调整为25cm，打开最大角度时，点H卡在隔板上，如图2所示，则可完全放入下方桶内的球体的直径不大于.

查看试题解析

三、解答题

17. 如图，在 $Rt △ A B C$ 中， $∠ B A C = 90 °$ ，AD是BC边上的高，若 $\sin ∠ C A D = \frac{3}{5}$ ， $B C = 25$ ，求AC的长．

查看试题解析
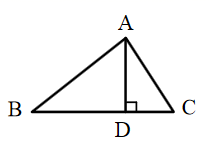18. 如图，在Rt△ABC中，∠ACB＝90°，sinB＝ $\frac{3}{5}$ ， D是BC上一点，DE⊥AB于点E，CD＝DE，AC+CD＝9.求BE，CE的长.

查看试题解析
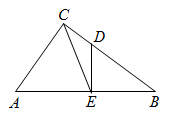19. 如图，AD是△ABC的高， $\cos B = \frac{\sqrt{2}}{2} ， \sin C = \frac{3}{5} ， A C = 10$ ，求△ABC的周长.

查看试题解析

四、综合题

20. 某小区外面的一段长120米的街道上要开辟停车位，计划每个停车位都是同样的长方形且每个长方形的宽均为2.2米，如果长方形的较长的边与路段的边平行，如图1所示，那么恰好能够停放24辆车．（备注： $\sqrt{2} = 1.414$ ， $\sqrt{3} = 1.732$ ， $\sqrt{5} = 2.236$ ）

(1)、如果长方形的边与街道的边缘成45°角，那么按图1，图2中的方法停放，一个停车位占用街道的长度各是多少？（结果保留一位小数）

(2)、如果按照图2中的方法停放车辆，这段路上最多可以停放多少车辆？

查看试题解析
21. 如图，在△ABC中，AD是BC上的高，BD＝AC＝10，tanB＝ $\frac{4}{5}$ ．

(1)、求AD的长；

(2)、求cos∠C的值和S_△ABC ．

查看试题解析
22. 已知：如图，在 $△ A B C$ 中， $A B = 6$ ， $B C = 8$ ， $∠ B = 60^{\circ}$ .求：

(1)、 $△ A B C$ 的面积；

(2)、 $∠ C$ 的余弦值.

查看试题解析