湘教版初中数学九年级上学期期末复习专题13 正切
试卷更新日期:2021-12-10 类型:复习试卷
一、单选题
-
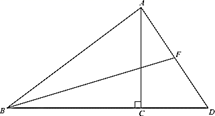
1. 的值为( )A、1 B、 C、2 D、2. 如图, 中, 于点D,若 , ,则 的值为( )
 A、 B、 C、 D、3. 如图,在平面直角坐标系 中,直线 与y轴交于点C , 与反比例函数 在第一象限内的图象交于点B , 连接 ,若 ,则 的值是( )
A、 B、 C、 D、3. 如图,在平面直角坐标系 中,直线 与y轴交于点C , 与反比例函数 在第一象限内的图象交于点B , 连接 ,若 ,则 的值是( ) A、 B、 C、2 D、34. 下列计算正确的是( )A、(π﹣3)0=1 B、tan30°= C、 =±2 D、a2•a3=a65. 如图,在△ABC中,点O是角平分线AD、BE的交点,若AB=AC=10,BC=12,则tan∠OBD的值是( )
A、 B、 C、2 D、34. 下列计算正确的是( )A、(π﹣3)0=1 B、tan30°= C、 =±2 D、a2•a3=a65. 如图,在△ABC中,点O是角平分线AD、BE的交点,若AB=AC=10,BC=12,则tan∠OBD的值是( ) A、 B、2 C、 D、6. 如图,点A、B、C在边长为1的正方形网格格点上,下列结论错误的是( )
A、 B、2 C、 D、6. 如图,点A、B、C在边长为1的正方形网格格点上,下列结论错误的是( ) A、sinB B、sinC C、tanB D、sin2B+sin2C=17. 如图,矩形AOBC的顶点A、B在坐标轴上,点C的坐标是(﹣10,8),点D在AC上,将 BCD沿BD翻折,点C恰好落在OA边上点E处,则tan∠DBE等于( )
A、sinB B、sinC C、tanB D、sin2B+sin2C=17. 如图,矩形AOBC的顶点A、B在坐标轴上,点C的坐标是(﹣10,8),点D在AC上,将 BCD沿BD翻折,点C恰好落在OA边上点E处,则tan∠DBE等于( )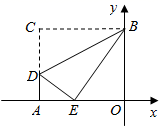 A、 B、 C、 D、8. 如图,在正方形方格纸中,每个小的四边形都是相同的正方形,点 , , , 都在格点处, 与 相交于点 ,则 的值是( )
A、 B、 C、 D、8. 如图,在正方形方格纸中,每个小的四边形都是相同的正方形,点 , , , 都在格点处, 与 相交于点 ,则 的值是( ) A、 B、 C、 D、9. 计算 的值为( )A、 B、0 C、 D、10. 在正方形 中, ,点E是 边的中点,连接 ,延长 至点F , 使得 ,过点F作 ,分别交 、 于N、G两点,连接 、 、 ,下列正确的是( )
A、 B、 C、 D、9. 计算 的值为( )A、 B、0 C、 D、10. 在正方形 中, ,点E是 边的中点,连接 ,延长 至点F , 使得 ,过点F作 ,分别交 、 于N、G两点,连接 、 、 ,下列正确的是( )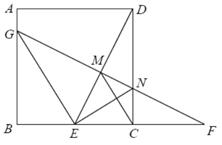
① ; ② ; ③ ; ④ .
A、4 B、3 C、2 D、1二、填空题
-
11. 已知 是锐角, ,则 =°.12. 已知:正方形ABCD的边长为3,点P是直线CD上一点,若DP=1,则tan∠BPC的值是 .13. 如下图:直角三角形纸片的两直角边长分别为4,8,现将△ABC如图那样折叠,使点A与点B重合,折痕为DE,则 的值是 .
 14. 如图的正方形网格中, 的顶点都在格点上,则 值为.
14. 如图的正方形网格中, 的顶点都在格点上,则 值为.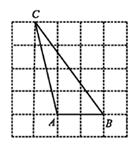 15. 在直角 中, , , 的角平分线交 于点 ,且 ,斜边 的值是.16. 如图,Rt△ABC中,∠BAC=90°,tan∠ABC= ,将△ABC绕A点顺时针方向旋转角α(0°<α<90°)得到△AB′C′,连接BB′,CC′,则△CAC′与△BAB′的面积之比等于 .
15. 在直角 中, , , 的角平分线交 于点 ,且 ,斜边 的值是.16. 如图,Rt△ABC中,∠BAC=90°,tan∠ABC= ,将△ABC绕A点顺时针方向旋转角α(0°<α<90°)得到△AB′C′,连接BB′,CC′,则△CAC′与△BAB′的面积之比等于 .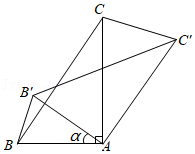
三、作图题
-
17. 如图,方格纸中每个小正方形的边长均为1,线段 的端点在小正方形的顶点上.分别画出符合要求的图形,所画图形各顶点必须与方格纸中的小正方形顶点重合.
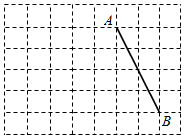 (1)、在图中画出以 为腰的等腰直角三角形 ;(2)、在图中画出面积为6的等腰三角形 ,并直接写出 的值.18. 如图,在 的正方形网格中,A,B,C,E均为小正方形的顶点,用无刻度的直尺画图,保留画图痕迹.
(1)、在图中画出以 为腰的等腰直角三角形 ;(2)、在图中画出面积为6的等腰三角形 ,并直接写出 的值.18. 如图,在 的正方形网格中,A,B,C,E均为小正方形的顶点,用无刻度的直尺画图,保留画图痕迹. (1)、将线段 绕点A逆时针旋转 得到线段 ;(2)、在 上画点T,使 ;(3)、在 上画点F(不与点C重合),使 ;(4)、在 上画点N,使 .
(1)、将线段 绕点A逆时针旋转 得到线段 ;(2)、在 上画点T,使 ;(3)、在 上画点F(不与点C重合),使 ;(4)、在 上画点N,使 .四、解答题
-
19. 如图,在Rt△ABC中,∠C=90°,AB=10,BC=6,求sinA,cosA,tanA的值.
 20. 先化简,再求值: ,其中 .21. 如图,在 中, , , .求: 、 .
20. 先化简,再求值: ,其中 .21. 如图,在 中, , , .求: 、 .
五、综合题