湘教版初中数学九年级上学期期末复习专题12 正弦和余弦
试卷更新日期:2021-12-10 类型:复习试卷
一、单选题
-
1. 在Rt△ABC中,∠C=90°,AC=4,BC=3,那么∠B的余弦值是( )A、 B、 C、 D、2. 在直角三角形中,各边的长度都扩大3倍,则锐角A的三角函数值( )A、也扩大3倍 B、缩小为原来的 C、都不变 D、有的扩大,有的缩小3. 如图,边长为10的等边 中,点 在边 上,且 ,将含30°角的直角三角板( )绕直角顶点 旋转, 、 分别交边 、 于 、 .连接 ,当 时, 长为( )
 A、6 B、 C、10 D、4. 如图,△ABC中,cosB ,sinC ,AC=5,则△ABC的面积是( )
A、6 B、 C、10 D、4. 如图,△ABC中,cosB ,sinC ,AC=5,则△ABC的面积是( )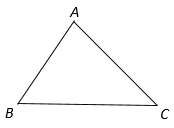 A、 B、12 C、14 D、215. 如图,在边长为4的正方形ABCD中,点E是CD边上的一点,点F是点D关于直线AE对称的点,连接AF、BF,若tan∠ABF=2,则DE的长是( )
A、 B、12 C、14 D、215. 如图,在边长为4的正方形ABCD中,点E是CD边上的一点,点F是点D关于直线AE对称的点,连接AF、BF,若tan∠ABF=2,则DE的长是( ) A、1 B、 C、 D、6. 如图,点A、B、C均在小正方形的顶点上,且每个小正方形的边长均为1,则cos∠BAC的值为( )
A、1 B、 C、 D、6. 如图,点A、B、C均在小正方形的顶点上,且每个小正方形的边长均为1,则cos∠BAC的值为( )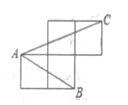 A、 B、 C、1 D、7. 在△ABC中,若|sinA- |+( -cosB)2=0,则∠C的度数是( )A、45° B、75° C、105° D、120°8. 如图是一张高脚木凳,AC∥EF∥GH,AB=CD,点E,G是AB的三等分点,已知EF与GH之间的距离为25cm,∠EGH=80°,则椅脚AB的长度为 cm( )
A、 B、 C、1 D、7. 在△ABC中,若|sinA- |+( -cosB)2=0,则∠C的度数是( )A、45° B、75° C、105° D、120°8. 如图是一张高脚木凳,AC∥EF∥GH,AB=CD,点E,G是AB的三等分点,已知EF与GH之间的距离为25cm,∠EGH=80°,则椅脚AB的长度为 cm( ) A、 B、75sin80° C、 D、9. 已知 是锐角三角形,若 ,则( )A、 B、 C、 D、10. 已知在 中, , , ,则 的长为( )A、 B、 C、 D、11. 如图,在平面直角坐标系中,点A的坐标为(4,3),那么cosα的值是( )
A、 B、75sin80° C、 D、9. 已知 是锐角三角形,若 ,则( )A、 B、 C、 D、10. 已知在 中, , , ,则 的长为( )A、 B、 C、 D、11. 如图,在平面直角坐标系中,点A的坐标为(4,3),那么cosα的值是( ) A、 B、 C、 D、12. 西周时期,丞相周公旦设置过一种通过测定日影长度来确定时间的仪器,称为圭表.如图是一个根据北京的地理位置设计的圭表,其中,立柱AC高为a.已知,冬至时北京的正午日光入射角∠ABC约为26.5°,则立柱根部与圭表的冬至线的距离(即BC的长)约为( )
A、 B、 C、 D、12. 西周时期,丞相周公旦设置过一种通过测定日影长度来确定时间的仪器,称为圭表.如图是一个根据北京的地理位置设计的圭表,其中,立柱AC高为a.已知,冬至时北京的正午日光入射角∠ABC约为26.5°,则立柱根部与圭表的冬至线的距离(即BC的长)约为( ) A、 B、asin26.5° C、acos26.5° D、
A、 B、asin26.5° C、acos26.5° D、二、填空题
-
13. 在△ABC中,AB=AC,BD⊥AC于D,若cos∠BAD= ,BD= ,则CD的长为 .14. 在△ABC中,AB=AC,BD⊥AC于D,若cos∠BAD= ,BD= ,则CD为15. 如图,在边长为6的等边△ABC中,点D在边AB上,且AD=2,长度为1的线段PQ在边AC上运动,则线段DP的最小值为 , 四边形DPQB面积的最大值为 .
 16. 如图,已知在 中, , , ,点 在边 上,将 沿着过点 的一条直线翻折,使点 落在边 上的点 处,连结 , ,若 ,则 的长是.
16. 如图,已知在 中, , , ,点 在边 上,将 沿着过点 的一条直线翻折,使点 落在边 上的点 处,连结 , ,若 ,则 的长是. 17. 如图,在 中,AD=3,AB=5, ,将 绕着点B顺时针旋转 后,点A的对应是点 ,联结 ,如果 ,那么 的值是 .
17. 如图,在 中,AD=3,AB=5, ,将 绕着点B顺时针旋转 后,点A的对应是点 ,联结 ,如果 ,那么 的值是 .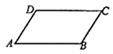 18. 如图,O是坐标原点,边长为2的菱形OABC的顶点C在x轴的负半轴上,cos∠AOC= ,函数 的图象经过顶点B,则k的值为.
18. 如图,O是坐标原点,边长为2的菱形OABC的顶点C在x轴的负半轴上,cos∠AOC= ,函数 的图象经过顶点B,则k的值为.
三、作图题
-
19. 如图,在平面直角坐标系中,已知 三个顶点的坐标分别是 , , .

( 1 )画出 向左平移6个单位长度后得到的 ;
( 2 )以点 为位似中心,将 缩小为原来的 ,得到 ,请在y轴右侧画出 ,并直接写 的值.
(不写解答过程,直接写结果,保留作图痕迹.)
四、解答题
-
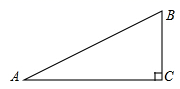
20. 如图,在 中, , , .求 的三个三角函数值.
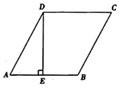
 21. 已知:如图,在菱形ABCD中,DE⊥AB于E,BE=16cm,
21. 已知:如图,在菱形ABCD中,DE⊥AB于E,BE=16cm,求此菱形的周长.
五、综合题
-
22. 如图,在△ABC中,CD是AB边上的中线,∠B=45°,tan∠ACB=3,AC= .
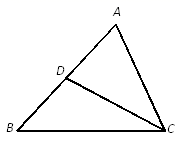
求:
(1)、△ABC的面积;(2)、sin∠ACD的值.23. 我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图①,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA ,容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题: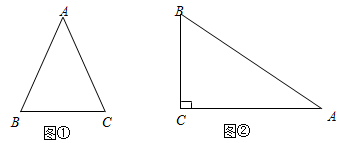 (1)、sad60°= , sad120°=(2)、如图②,在Rt△ABC中,∠ACB=90°,已知sinA ,试求sadA的值.(3)、直线y x+6与x轴,y轴分别交于点A,B,点M,N分别在线段AB,OA上,且△MON是等腰三角形,设△MON的顶角为θ,当sadθ 时,求点M的坐标.(请直接㝍出结果)24.(1)、计算:3tan30°-(cos60°)-1+ cos45°+(2)、先化简,再求代数式 的值,其中x=4cos30°-tan45°
(1)、sad60°= , sad120°=(2)、如图②,在Rt△ABC中,∠ACB=90°,已知sinA ,试求sadA的值.(3)、直线y x+6与x轴,y轴分别交于点A,B,点M,N分别在线段AB,OA上,且△MON是等腰三角形,设△MON的顶角为θ,当sadθ 时,求点M的坐标.(请直接㝍出结果)24.(1)、计算:3tan30°-(cos60°)-1+ cos45°+(2)、先化简,再求代数式 的值,其中x=4cos30°-tan45°
-