浙江省杭州市拱墅区锦绣育才教育集团2021-2022学年七年级上学期数学期中考试试卷

试卷更新日期：2021-12-10 类型：期中考试

进入出卷网下载

一、选择题（共10小题，每小题3分，满分30分）

1. 如果“盈利5%”记作+5%，那么-3%表示 $($ $)$

A、少赚3% B、亏损-3% C、盈利3% D、亏损3%

查看试题解析
2. 下列四个运算，结果最小的是 $($ $)$

A、 $1 + (- 3)$ B、 $1 - (- 3)$ C、 $1 \times (- 3)$ D、 $1 \div (- 3)$

查看试题解析
3. 下列各数中是无理数的是 $($ $)$

A、0 B、 $\frac{π}{2}$ C、-3.1415 D、 $\frac{22}{7}$

查看试题解析
4. 代数式 $\frac{a}{b + 2}$ 表示（）

A、a 除以 $b + 2$ B、 $b + 2$ 除a C、b与2的和除以a D、a除以b与2的和所得的商

查看试题解析
5. 下列计算正确的是（）

A、 $\sqrt{0.09} = \pm 0.3$ B、 $\sqrt{4 \frac{1}{4}} = 2 \sqrt{\frac{1}{2}}$ C、 $\sqrt[3]{- 27} = - 3$ D、 $- \sqrt{| - 25 |} = 5$

查看试题解析
6. 下列计算正确的是（）

A、 $5 a - 2 a = 3$ B、 $2 a + 3 b = 5 a b$ C、 $3 a + 2 a = 5 a^{2}$ D、 $- 3 a b + b a = - 2 a b$

查看试题解析
7. 下列说法错误的是 $($ $)$

A、代数式 $m + 5$ ， $m b$ ， $- 2$ 都是整式 B、单项式 $- a b$ 的系数是 $- 1$ ，次数是1 C、多项式 $3 x - π$ 的项是 $3 x$ ， $- π$ D、多项式 $5 x^{2} y - 2 x y + 4 x$ 是三次三项式

查看试题解析
8. 下列说法：①0是最小的整数；②最大的负整数是 $- 1$ ；③正有理数和负有理数统称为有理数；④立方等于它本身的数只有0，1.其中正确的是 $($ $)$

A、①②③④ B、①③④ C、②④ D、②

查看试题解析
9. 点 $A$ ， $B$ ， $C$ ， $D$ 在数轴上的位置如图所示，点 $A$ ， $D$ 表示的数互为相反数，若点 $B$ 表示的数为 $m$ ， $A$ ， $B$ 之间的距离为3，则点 $D$ 所表示的数为 $($ $)$

A、 $3 - m$ B、 $3 + m$ C、 $m - 3$ D、 $- m - 3$

查看试题解析
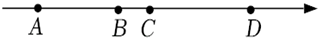10. 有两桶水，甲桶装有 $a$ 升水，乙桶中的水比甲桶中的水多3升.现将甲桶中倒一半到乙桶中，然后再将此时乙桶中总水量的 $\frac{1}{3}$ 倒给甲桶，假定桶足够大，水不会溢出.我们将上述两个步骤称为一次操作，进行重复操作，则 $($ $)$

A、每操作一次，甲桶中的水量都会减小，最后甲桶中的水会全部倒入乙桶 B、每操作一次，甲桶中的水量都会减小，但永远倒不完 C、每操作一次，甲桶中的水量都会增加，反复操作，最后甲桶中的水会比乙桶多 D、每操作一次，甲桶中的水量都会增加，但永远比乙桶中的水量要少

查看试题解析

二、填空题（共6小题，每小题4分，满分24分）

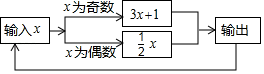
11. 数据10000用科学记数法表示为 .

查看试题解析
12. 用“ $>$ ”或“ $<$ ”填空：

(1)、 $| - 1 |$ 0；

(2)、 $- \frac{2}{3}$ $- \frac{5}{7}$ .

查看试题解析
13. 某种商品原价每件b元，第一次降价打八折，第二次降价每件又减10元，第二次降价后的售价是元．

查看试题解析
14. 下列5个等式：① $a b = 0$ ；② $a + b = 0$ ；③ $a^{2} = 0$ ；④ $a^{2} + b^{2} = 0$ ；⑤ $\sqrt{a} + \sqrt{b} = 0$ ， $a$ 一定是零的等式序号为.

查看试题解析
15. 当 $x = - 1$ 时，代数式 $a x^{2} + b x + 1$ 的值为 $- 1$ ，则 $(1 + a - b) (1 - a + b)$ 的值为 .

查看试题解析
16. 有一个数值转换器，原理如图所示，若开始输入 $x$ 的值是5，可发现第1次输出的结果是16，第2次输出的结果是8，第3次输出的结果是，依次继续下去，则第107次输出的结果是 .

查看试题解析

三、解答题（共7小题，满分66分）

17. 计算

(1)、 $\sqrt{9} + \sqrt[3]{- 8} + | - 4 |$ ；

(2)、 $- 1^{6} - (\frac{1}{4} - \frac{7}{8}) \times {(- 4)}^{3}$ .

查看试题解析
18.

(1)、如果 $| m - 4 | + {(n + 5)}^{2} = 0$ ，求 ${(m + n)}^{2021} + m^{3}$ 的值.

(2)、已知实数 $a$ ， $b$ ， $c$ ， $d$ ， $e$ ，且 $a$ ， $b$ 互为倒数， $c$ ， $d$ 互为相反数， $e$ 的绝对值为2，求 $\frac{1}{2} a b + \frac{c + d}{7} + e^{2}$ 的值.

查看试题解析
19. 先化简，再求值：

(1)、 $\frac{2}{3} y - 12 (- x + \frac{1}{3} y^{2}) + 6 (- \frac{3}{2} x + \frac{2}{3} y^{2})$ ，其中 $x = - 1 ， y = \frac{3}{2}$ .

(2)、 $(18 a - 3 a^{2}) - 5 (1 + 2 a + a^{2})$ ，其中 $a^{2} - a + 3 = 0$ .

查看试题解析
20. 老师写出一个整式 $(a x^{2} + b x - 1) - (4 x^{2} + 3 x)$ （其中 $a$ ， $b$ 为常数，且表示为系数），然后让同学给 $a$ ， $b$ 赋予不同的数值进行计算.

(1)、甲同学给出了 $a = 5$ ， $b = - 1$ ，请按照甲同学给出的数值化简整式；

(2)、乙同学给出一组数，计算的最后结果与 $x$ 的取值无关，求 $a$ ， $b$ 的值.

查看试题解析
21. 如图 $4 \times 4$ 方格（每个小正方形的边长均为1个单位长度）；

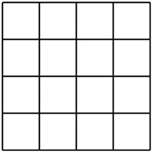(1)、在方格中作出面积为10平方单位的正方形；

(2)、估计该正方形边长的值在哪两个相邻整数之间；

(3)、在数轴上表示实数 $\sqrt{10}$ .

查看试题解析

22. 如图所示为一套住房的平面图.

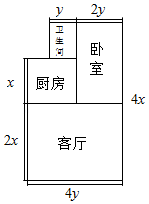(1)、请你表示卫生间和厨房的面积和；

(2)、请你用代数式表示住房的面积；

(3)、若

x = 3

，

y = 2

，求住房的面积；

(4)、在（3）问的条件下现准备铺设地面，卧室和客厅铺设地板，卫生间和厨房铺设地砖，按市场价格，地板单价为300元平方米，地砖单价为100元平方米，装修公司有

A

、

B

两种活动方案，如表：

活动方案	木地板价格	地砖价格	总安装费
$A$	8折	8.5折	2000元
$B$	9折	8.5折	免收

则小方家应选择哪种活动，使铺设地面总费用（含材料费及安装费）更低？

查看试题解析

23. 已知 $a > b$ ， $a$ 与 $b$ 两个数在数轴上对应的点分别为点 $A$ 、点 $B$ ，求 $A$ 、 $B$ 两点之间的距离.
【探索】

小明利用绝对值的概念，结合数轴，进行探索：因为 $a > b$ ，则有以下情况：

情况一、若 $a > 0$ ， $b ⩾ 0$ ，如图， $A$ 、 $B$ 两点之间的距离： $A B = | a | - | b | = a - b$ ；

$\dots \dots$

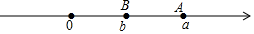(1)、补全小明的探索

(2)、【应用】
若点 $C$ 对应的数 $c$ ，数轴上点 $C$ 到 $A$ 、 $B$ 两点的距离相等，求 $c$ .（用含 $a$ 、 $b$ 的代数式表示）

(3)、若点 $D$ 对应的数 $d$ ，数轴上点 $D$ 到 $A$ 的距离是点 $D$ 到 $B$ 的距离的 $n (n > 0)$ 倍，请探索 $n$ 的取值范围与点 $D$ 个数的关系，并直接写出 $a$ 、 $b$ 、 $d$ 、 $n$ 的关系.

查看试题解析