浙江省杭州市六校2021-2022学年九年级上学期数学期中联考试卷

试卷更新日期：2021-12-10 类型：期中考试

进入出卷网下载

一、选择题：本大题有10小题，每小题3分，共30分.

1. 下列图形中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 二次函数y＝（x﹣1）²﹣3的顶点坐标是（）

A、（1，﹣3） B、（﹣1，﹣3） C、（1，3） D、（﹣1，3）

查看试题解析
3. 下列说法正确的是（）

A、“明天下雨的概率为99%”，则明天一定会下雨 B、“367人中至少有2人生日相同”是随机事件 C、抛掷10次硬币，7次正面朝上，则抛掷硬币正面朝上的概率为0.7 D、“抛掷一枚均匀的骰子，朝上的面点数为偶数”是随机事件

查看试题解析
4. 已知⊙O的半径为2，点P到圆心O的距离为 $\sqrt{3}$ ，则点P在（）

A、圆内 B、圆上 C、圆外 D、不能确定

查看试题解析
5. 设A（2，y₁），B（3，y₂），C（﹣4，y₃）是抛物线y＝ax²﹣2ax+c（a＞0）图象上的三点，则y₁ ， y₂ ， y₃的大小关系为（）

A、y₃＞y₂＞y₁ B、y₃＞y₁＞y₂ C、y₂＞y₁＞y₃ D、y₁＞y₃＞y₂

查看试题解析
6. 下列有关圆的一些结论：①平分弧的直径垂直于弧所对的弦；②平分弦的直径垂于于弦；③在同圆或等圆中，相等的弦对应的圆周角相等；④同弧或等弧所对的弦相等.其中正确的有（）

A、①③ B、①④ C、②④ D、①②④

查看试题解析
7. 已知二次函数y=kx²﹣7x﹣7的图象和x轴有交点，则k的取值范围是（）

A、k＞﹣ $\frac{7}{4}$ B、k≥﹣ $\frac{7}{4}$ C、k≥﹣ $\frac{7}{4}$ 且k≠0 D、k＞﹣ $\frac{7}{4}$ 且k≠0

查看试题解析
8. 如图，在⊙O中，AB为直径，点C为圆上一点，将劣弧沿弦AC翻折交AB于点D，连接CD.若点D与圆心O不重合，∠BAC＝26°，则∠DCA的度数为（）

A、36° B、38° C、40° D、42°

查看试题解析
9. 二次函数y＝x²+bx的对称轴为直线x＝2，若关于x的一元二次方程x²+bx﹣t＝0（t为实数）在﹣1＜x≤6的范围内有解，则t的取值范围是（）

A、5＜t≤12 B、﹣4≤t≤5 C、﹣4＜t≤5 D、﹣4≤t≤12

查看试题解析
10. 如图，⊙O是以坐标原点O为圆心， $4 \sqrt{2}$ 为半径的圆，点P的坐标为（2，2），弦AB经过点P，则图中阴影部分面积的最小值为（）

A、8π B、 $\frac{32}{3} π$ C、8π﹣16 D、 $\frac{32}{3} π - 8 \sqrt{3}$

查看试题解析

二、填空题：本大题有6个小题，每小题4分，共24分。

11. 一个多边形的每个外角都是45°，则这个多边形的边数为．

查看试题解析
12. 在平面直角坐标系中，将二次函数y＝﹣x²的图象向左平移2个单位长度，再向上平移1个单位长度所得抛物线对应的函数表达式为 .

查看试题解析
13. 如图，四边形ABCD内接于⊙O，已知∠ADC＝140°，则∠AOC＝°.

查看试题解析
14. 在一个不透明的口袋中，装有若干个红球和4个黄球，它们除颜色外没有任何区别，摇匀后从中随机抽出一个球.记下颜色后再放回口袋中，通过大量重复摸球试验发现，摸到黄球的频率是0.2，则估计盒子中大约有红球个.

查看试题解析
15. 已知二次函数y＝x²+bx+c中，函数y与自变量x的部分对应值如表：

x

…

0

1

2

3

…

y

…

5

2

1

2

…

若A（m，y₁），B（m+6，y₂）两点都在该函数图象上，当y₁＞y₂时，m的取值范围是 .

查看试题解析
16. 对于二次函数y＝﹣x²+2（m+1）x+6m+4.下列说法正确的有：（填序号）.
①函数图象开口向下；

②当x≥m时，y随x的增大而减小；

③函数图象过定点（﹣3，﹣11）；

④若不等式 $\frac{x^{2} - 8 x + 20}{- x^{2} + 2 (m + 1) x + 6 m + 4}$ ＜0的解集为全体实数，则﹣4﹣ $\sqrt{11}$ ＜m＜﹣4+ $\sqrt{11}$ .

查看试题解析

三、解答题（本大题有7个小题，共66分。）

17. 如图，在△ABC中∠C＝90°；

(1)、画出将△ABC绕点C逆时针旋转90°所得到的△A₁B₁C₁；

(2)、若BC＝3，求点B运动到点B₁所经过的路线长度.

查看试题解析
18. 如图所示的转盘，三个扇形的圆心角相等，分别标有数字1，2，3.小明和小亮进行一个游戏，游戏规则为：一人转动一次圆盘，如果两次转出的数字之和为偶数，那么小明胜；否则小亮胜.

(1)、用画树状图或列表的方法求出小明获胜的概率；

(2)、你认为该游戏公平吗？请说明理由.

查看试题解析
19. 如图，抛物线分别经过点A（﹣2，0），B（3，0），C（1，6）.

(1)、求抛物线的函数解析式；

(2)、求当y＞4时，自变量x的取值范围.

查看试题解析
20. 如图，AB是⊙O的直径，点C，D是⊙O上的点，且OD∥BC，AC分别与BD，OD相交于点E，F.

(1)、求证：点D为 $\overset{⌢}{A C}$ 的中点；

(2)、若DF＝7，AC＝24，求⊙O的直径.

查看试题解析
21. 在校园嘉年华中，九年级同学将对一块长20m，宽10m的场地进行布置，设计方案如图所示.阴影区域为绿化区（四块全等的矩形），空白区域为活动区，且4个出口宽度相同，其宽度不小于4m，不大于8m.设出口长均为x（m），活动区面积为y（m²）.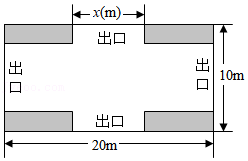

(1)、求y关于x的函数表达式；

(2)、当x取多少时，活动区面积最大？最大面积是多少？

(3)、若活动区布置成本为10元/m² ，绿化区布置成本为8元/m² ，布置场地的预算不超过1850元，当x为整数时，请求出符合预算且使活动区面积最大的x值及此时的布置成本.

查看试题解析
22. 已知二次函数y₁＝ax²+bx+2（a＞0，b＞0）的图象与x轴只有一个交点A，与y轴交于点B，一次函数y₂＝x+k经过点B.

(1)、当a＝1时，求点A的坐标；

(2)、当a＝2时，若y₁＜y₂ ，求x的取值范围；

(3)、若y₁与y₂图象的另一交点是P，当b≥1时，求点P横坐标p的取值范围.

查看试题解析
23. 如图，△ABC内接于⊙O，∠A＝60°，BE⊥AC于点E，延长线交⊙O于点P.

(1)、如图①，若△ABC是等边三角形，求证：OE＝PE；

(2)、如图②，当点A在直线BC上方运动时（包括点B、C），作CQ⊥AB交BE于点H，
①求证：HE＝PE；

②若BC＝3，求点H运动轨迹的长度.

查看试题解析

x	…	0	1	2	3	…
y	…	5	2	1	2	…