浙江省杭州十五中教育集团2021-2022学年九年级上学期数学期中考试试卷
试卷更新日期：2021-12-10 类型：期中考试
一、选择题（本题有10个小题，每小题3分，共30分）
-
1. 抛物线y＝（x﹣2）2﹣4的对称轴是（ ）A、直线x＝﹣2 B、直线x＝2 C、直线x＝﹣4 D、直线x＝42. 在一个不透明的布袋里装有白、红、黑三种颜色的小球，它们除颜色外没有任何区别，其中白球1个，红球3个，黑球2个.将袋中的球搅匀，随机从中取出1个球，则取出黑球的概率是（ ）A、 B、 C、 D、3. 如图，四边形ABCD内接于圆O，∠DCE＝65°，则∠A的度数为（ ）
A、112° B、68° C、65° D、52°4. 抛物线的部分图象如图所示，它与x轴的一个交点坐标为（﹣3，0），对称轴为x＝﹣1，则它与x轴的另一个交点坐标为（ ）
A、（4，0） B、（3，0） C、（2，0） D、（1，0）5. 某射击运动员在同一条件下的射击成绩记录如下：射击次数
20
80
100
200
400
1000
“射中九环以上”的次数
18
68
82
168
327
823
“射中九环以上”的频率（结果保留两位小数）
0.90
0.85
0.82
0.84
0.82
0.82
根据频率的稳定性，估计这名运动员射击一次时“射中九环以上”的概率约是（ ）
A、0.90 B、0.82 C、0.85 D、0.846. 如图，⊙O是△ABC的外接圆，∠BAC＝60°，若⊙O的半径OC为2，则弦BC的长为（ ）
A、4 B、2 C、3 D、7. 如图，网格中的小正方形边长都是1，则以O为圆心，OA为半径的弧 和弦AB所围成的弓形面积等于（ ）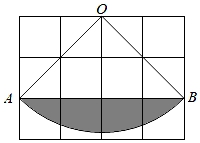
A、2π﹣4 B、2π﹣8 C、4π﹣4 D、π﹣48. 在3张反面无差别的卡片上，其正面分别印有等边三角形、平行四边形和正六边形.现将3张卡片的正面朝下放置，混合均匀后从中随机抽取两张，则抽到的卡片正面图形都是轴对称图形的概率为（ ）A、 B、 C、 D、9. 足球运动员将足球沿与地面成一定角度的方向踢出，足球飞行的路线是一条抛物线，不考虑空气阻力，足球距离地面的高度h（单位：m）与足球被踢出后经过的时间t（单位：s）之间的关系如表：t
0
1
2
3
4
5
6
7
…
h
0
8
14
18
20
20
18
14
…
下列结论：①足球距离地面的最大高度超过20m；②足球飞行路线的对称轴是直线t＝ ；③点（9，0）在该抛物线上；④足球被踢出5s～7s时，距离地面的高度逐渐下降.其中正确的结论是（ ）
A、②③ B、①②③ C、①②③④ D、②③④10. 已知y1和y2均是以x为自变量的函数，当x＝m时，函数值分别是M1和M2 ， 若存在实数m，使得M1+M2＝1，则称函数y1和y2具有性质P.以下函数y1和y2不具有性质P的是（ ）A、y1＝x2+2x和y2＝﹣x﹣1 B、y1＝x2+2x和y2＝﹣x+1 C、y1＝﹣ 和y2＝﹣x﹣1 D、y1＝﹣ 和y2＝﹣x+1二、填空题（本题有6个小题，每小题4分，共24分）
-
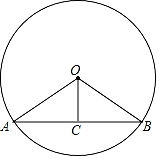
11. 二次函数y＝3x2的图象经过点A（﹣1，y1），B（2，y2），则y1y2.（填“＞”“＜”或“＝”）12. 从 ，0，π，这三个数中随机抽取一个数，恰好是无理数的概率是 .13. 如图，已知在半径为10的⊙O中，弦AB＝16，OC⊥AB，则OC的长为 .
14. 给出下列函数：①y＝2x﹣1；②y＝ ；③y＝﹣x2中，符合条件“当x＞0时，函数值随x增大而减小”的函数是 （填序号）.15. 如图，在正五边形ABCDE中，点F是DE的中点，连接CE与BF交于点G，则∠CGF＝°.
16. 已知二次函数y＝﹣x2+2x+5，若P（n，y1），Q（n﹣2，y2）是该二次函数图象上的两点，且y1＞y2 ， 则实数n的取值范围为 .三、解答题（本题有7个小题，共66分）
-
17. 已知二次函数y＝x2﹣4x+5.(1)、求出此二次函数图象的顶点坐标.(2)、求出y随x的增大而减小时，x的取值范围.18. 某校为了学生的身体健康，每天开展体育活动一小时，开设排球、篮球、羽毛球、跳绳课，学生可以根据自己的爱好任选一项，老师根据学生报名情况进行了统计，并绘制了如图所示的尚未完成的频数分布直方图和扇形统计图，请你结合图中的信息，解答下列问题.
(1)、该校学生报名总人数有多少人？(2)、从表中可知选羽毛球的学生有多少人？选排球和篮球的人数分别占报名总人数的百分之几？并补全两个统计图；(3)、若从中随机抽一名学生，则该学生爱好跳绳的概率是多少？19. 如图，AB是⊙O的直径，点C、D均在⊙O上，∠ACD＝30°，弦AD＝4cm ．
(1)、求⊙O的直径．(2)、求 的长．20. 小明、小军两同学做游戏，游戏规则是：一个不透明的文具袋中，装有型号完全相同的2支红笔和1支黑笔，一人从袋中取出一支笔，放回，另一人再从中随机取出一支笔，若两人所取笔的颜色相同，则小明胜；否则，小军胜.(1)、若小明第一个取笔，求他能取到红笔的概率；(2)、请用概率知识判断这个游戏是否公平？若不公平，您认为对谁有利.21. 某书店销售一本畅销的小说，每本进价为20元，根据以往经验，当销售单价是25元时，每天的销售量是250本；销售单价每上涨1元，每天的销售量就减少10本.(1)、请求出书店销售该小说每天的销售量y（本）与销售单价x（元）之间的函数关系式；(2)、每本小说售价为多少元时，书店所得利润最大？最大利润是多少元？
