贵州省黔西南布依族苗族自治州2021-2022学年七年级上学期数学期中考试试卷

试卷更新日期：2021-12-10 类型：期中考试

进入出卷网下载

一、单选题

1. ﹣2021的相反数是（　　）

A、﹣2021 B、2021 C、﹣ $\frac{1}{2021}$ D、 $\frac{1}{2021}$

查看试题解析
2. 根据第七次人口普查数据，截至2020年11月1日零时，黔西南布依族苗族自治州常住人口约为3015100人，将数据3015 100用科学记数法表示为（）

A、0.30151×10⁸ B、3.0151×10⁶ C、301.51×10⁴ D、30151×10²

查看试题解析
3. 下列关于多项式2m²－4m＋1的说法中，正确的是（）

A、二次项是－4m B、是三次三项式 C、一次项系数是－4 D、最高次项是2

查看试题解析
4. 下列运算正确的是（）

A、 $3^{2} = 6$ B、 $- 6 a - 6 a = 0$ C、 $- 4^{2} = - 16$ D、 $- 5 x y + 2 x y = - 3$

查看试题解析
5. 乐乐做了以下四道计算题：①－（－3）＋4＝1；②0－（－1）＝－1；③（－ $\frac{1}{2}$ ）× $\frac{1}{3}$ ＝－ $\frac{1}{6}$ ；④－（－ $\frac{1}{3}$ ）÷（－ $\frac{1}{2}$ ）＝－ $\frac{2}{3}$ ，请你帮他检查一下，他一共做对了（）

A、1道 B、2道 C、3道 D、4道

查看试题解析
6. 已知b－a＝10，c＋d＝－5，则（b＋c）－（a－d）的值为（）

A、－5 B、15 C、－15 D、5

查看试题解析
7. 已知多项式2x³－8x²＋x－1与多项式3x³＋2mx²－5x＋3的和不含二次项，则m的值为（）

A、－4 B、－2 C、2 D、4

查看试题解析
8. -a、b两数在数轴上的位置如图，下列结论正确的是（）

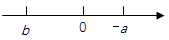A、a＞0，b＜0 B、a＜b C、 $| a | = - a$ ， $| b | = - b$ D、 $| a |$ ＞ $| b |$

查看试题解析
9. 当 $x = 1$ 时，多项式 $a x^{3} + b x - 2$ 的值为2，则当 $x = - 1$ 时，该多项式的值是（）

A、 $- 6$ B、 $- 2$ C、0 D、2

查看试题解析
10. 3²⁰²¹的末位数字是（）

A、 1 B、3 C、7 D、9

查看试题解析

二、填空题

11. 黔西南州金州大桥的建设工作正在如火如荼地进行着，预计2023年建成通车，大桥起点位于兴义侧峡谷大道与万峰林大道交叉口，终点位于义龙新区顶效侧桥台后117m处，与义龙新区东峰林大道对接，道路全长2912.787m，把2912.787精确到十分位可以表示为

查看试题解析
12. 把多项式2m²﹣4m⁴+2m﹣1按m的升幂排列．

查看试题解析
13. 一台无人机从高度为 $50 m$ 的位置开始，先上升 $10 m$ ，后下降 $18 m$ ，此时这台无人机所在的高度是 $m$ .

查看试题解析
14. 若|a|=4，–b=3，则a+b=.

查看试题解析
15. 若－3x²y¹^－n与x^my³是同类项，则m＋n＝

查看试题解析
16. 如图，长方形纸片上画有三个完全相同的阴影长方形，那么剩余的非阴影长方形的周长为（用含a，b的代数式表示）.

查看试题解析
17. 已知 $3 x^{2} + 2 x - 3$ 的值为6，则 $2 - x^{2} - \frac{2}{3} x$ 的值为．

查看试题解析
18. 计算： $1 + 2 - 3 - 4 + 5 + 6 - 7 - 8 + 9 + 10 - 11 - 12 + \dots + 2018$ $- 2019 - 2020 + 2021 =$ .

查看试题解析
19. 如果规定 $a ※ b = \frac{a b - 1}{a + b} + 1$ ，则2※（－3）的值为．

查看试题解析
20. 若a，b，c为整数，且|a－b|＋|c－a|＝1，则|c－a|＋|a－b|＋|b－c|的值为

查看试题解析

三、解答题

21. 计算：

(1)、（－3）－（－2）＋（－4）＋（－9）；

(2)、－ $1^{2021}$ ＋ ${(- \frac{3}{2})}^{2}$ －（－4）÷ $\frac{1}{2}$

查看试题解析
22. 已知有理数a，b在数轴上的对应点的位置如图所示.

(1)、化简：|a|－|2a－b|－|a－b|；

(2)、当a＝－2，b＝1时，求代数式|a|－|2a－b|－|a－b|的值.

查看试题解析
23.

(1)、先化简，再求值：3（a²－2ab）－[a²－3b＋3（ab＋b）]，其中a＝－3，b＝ $\frac{1}{3}$ .

(2)、已知a，b互为相反数，c，d互为倒数，x的平方等于9，求 a＋b＋x－ $\frac{c d}{2}$ 的值.

查看试题解析
24. 小刘在某学校附近开了一家麻辣烫店，为了吸引顾客，于是想到了发送宣传单：刘氏麻辣烫开业大酬宾，第一周每碗4.5元，第二周每碗5元，第三周每碗5.5元，从第四周开始每碗6元.月末结算时，每周以50碗为标准，多卖的记为正，少卖的记为负，这四周的销售情况如下表（表中数据为每周每天的平均销售情况）：

周次

一

二

三

四

销售量

38

26

10

﹣4

(1)、若麻辣烫成本为3.1元/碗，哪一周的收益最多？是多少？

(2)、这四周总销售额是多少？

(3)、为了拓展学生消费群体，第四周后，小刘又决定实行两种优惠方案：
方案一：凡来店中吃麻辣烫者，每碗附赠一瓶0.7元的矿泉水；

方案二：凡一次性购买3碗以上的，可免费送货上门，但每次送货小刘需支付人工费2元.

若有人一次性购买4碗，小刘更希望以哪种方案卖出？

查看试题解析
25. 在解决数学问题的过程中，我们常用到"分类讨论"的数学思想，下面是运用"分类讨论"的数学思想解决问题的过程，请仔细阅读，并解答问题.
（提出问题）已知有理数a，b，c满足abc＞0，求 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 的值.

（解决问题）解∶由题意，得 a，b，c三个有理数都为正数或其中一个为正数，另两个为负数.

①当a，b，c都为正数，即a＞0，b＞0，c＞0时， $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ ＝ $\frac{a}{a} + \frac{b}{b} + \frac{c}{c}$ ＝1＋1＋1＝3

②当a，b，c中有一个为正数，另两个为负数时，不妨设a＞0，b＜0，c＜0，则 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ ＝ $\frac{a}{a} + \frac{- b}{b} + \frac{- c}{c}$ ＝1＋（－1）＋（－1）＝－1

综上所述， $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 的值为3或－1

（探究拓展）

请根据上面的解题思路解答下面的问题：

(1)、已知a，b是不为0的有理数，当|ab|＝－ab时， $\frac{a}{| a |} + \frac{b}{| b |}$ ＝

(2)、已知a，b，c是有理数，当abc＜0时，求 $\frac{a}{| a |} + \frac{b}{| b |}$ ＋ $\frac{c}{| c |}$ ＝

(3)、已知a，b，c是有理数，a＋b＋c＝0，abc＜0，求 $\frac{b + c}{| a |} + \frac{c + a}{| b |} + \frac{a + b}{| c |}$ ＝

查看试题解析

周次	一	二	三	四
销售量	38	26	10	﹣4