2021-2022学年浙教版数学八年级上册期末检测卷2

试卷更新日期：2021-12-10 类型：期末考试

进入出卷网下载

一、单选题

1. 下列命题中，是真命题的是（）

A、同一平面内，垂直于同一条直线的两条直线互相平行 B、三角形的一个外角大于三角形的每一个内角 C、同一平面内，两条直线的位置关系只有垂直和平行 D、面积相等的两个三角形全等

查看试题解析
2. 下列表述能确定物体具体位置的是（）

A、敬业小区 B、胜利南街右边 C、北偏东30° D、东经118°，北纬28°

查看试题解析
3. 如图，点P是△ABC内一点，PD⊥BC，PE⊥AC，PF⊥AB，且PD=PE=PF，则点P是△ABC（）

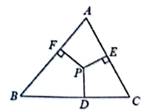A、三边垂直平分线的交点 B、三条角平分线的交点 C、三条高所在直线的交点 D、三条中线的交点

查看试题解析
4. 能说明命题“若a²＞b² ，则a＜b”是假命题的反例是（）

A、a=2，b=-1 B、a=-2，b=1 C、a=-1，b=2 D、a=1，b=-2

查看试题解析
5. 如图，长方形纸片ABC）沿对角线折叠，设重叠部分为△EBD，那么下列说法
正确的有（）

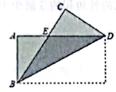
①△EBD是等腰三角形，EB=ED；

②折叠后∠ABE和∠CBD一定相等；

③折叠后得到的图形是轴对称图形

④△EBA和△EDC一定是全等三角形，

A、①③④ B、①②④ C、①②③ D、①②③④

查看试题解析
6. 如图，在△ABC中，∠B=40°，∠C=70°，AD是高，AE是角平分线，则∠DAE的度数为（）

A、10° B、15° C、20° D、25°

查看试题解析
7. 已知关于x的不等式组 ${\begin{matrix} x - a > 0 \\ 3 - 2 x > 0 \end{matrix}$ 的整数解共有3个，则a的取值范围是（）

A、﹣2≤a＜﹣1 B、﹣2＜a≤1 C、﹣2＜a＜﹣1 D、a＜﹣1

查看试题解析
8. 已知图形A在y轴的右侧，如果将图形A上的所有点的横坐标都乘﹣1，纵坐标不变得到图形B，则（）

A、两个图形关于x轴对称 B、两个图形关于y轴对称 C、两个图形重合 D、两个图形不关于任何一条直线对称

查看试题解析
9. 若一个正比例函数的图象经过点（2，-3），则这个图象一定也经过点（　　）

A、（-3，2） B、（ $\frac{3}{2}$ ，-1） C、（ $\frac{2}{3}$ ，-1） D、（- $\frac{3}{2}$ ，1）

查看试题解析
10. 如图所示，表示一次函数 $y = a x + b$ 与正比例函数 $y = a b x (a$ ， $b$ 是常数，且 $a b \neq 0)$ 的图象是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 举例说明命题“对于任意实数x，代数式 $x^{2} - 1$ 的值总是正数”是假命题，则x的值可以是.

查看试题解析
12. 由于木质衣架没有柔性，在挂置衣服的时候不太方便操作．小明设计了一种衣架，在使用时能轻易收拢，然后套进衣服后松开即可．如图1，衣架杆OA＝OB＝20cm，若衣架收拢时，∠AOB＝60°，如图2，则此时A，B两点之间的距离是cm．

查看试题解析
13. 下列命题中：
①若 $a > b$ ，则 $a - b < 0$ ；

②若 $a < 0$ ，则 $b - a > b$ ；

③若 $a > b$ ，则 $b c^{2} < a c^{2} (c \neq 0)$ ；

④若 $a x > - a$ ，则 $x > - 1$ ．

正确的有．（只填写正确命题的序号）

查看试题解析
14. 一次函数y= -2x+4的图象与坐标轴所围成的三角形面积是 .

查看试题解析
15. 如图所示的正方体木块的棱长为3cm，沿其相邻三个面的对角线（图中虚线）剪掉一角，得到如图②所示的几何体，一只蚂蚁沿着图②中的几何体表面从顶点A爬行到顶点B的最短距离为cm．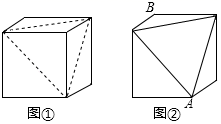

查看试题解析
16. 在平面直角坐标系xOy中，点A（﹣4，0），B（2，0）在x轴上，若点P到两坐标轴的距离相等，且∠APO＝∠BPO ，则点P的坐标为．

查看试题解析

三、解答题

17. 在平面直角坐标系中，正比例函数 $y = m x$ $(m \neq 0)$ 的图象经过点 $(m ， 4)$ ，且 $y$ 随 $x$ 的增大而减小，求该正比例函数的表达式.

查看试题解析
18. 如图，直线AB∥CD，点E在CD上，点O、点F在AB上，连接OE，过点F作FH⊥OE于点H.

(1)、尺规作图：作∠EOF的角平分线OG交CD于点G；（不写作法，保留作图痕迹，并标明字母）

(2)、在（1）的条件下，已知∠OFH＝20°，求∠OGD的度数.

查看试题解析
19.

(1)、解二元一次方程组 ${\begin{matrix} x + 2 y = 1 \\ 2 x + y = 5 \end{matrix}$ .

(2)、已知（1）中的解满足0＜ax+3y＜6.求正整数a的算术平方根.

查看试题解析
20. 已知关于x、y的二元一次方程组 ${\begin{matrix} 3 x - 5 y = 4 m \\ 5 x - 3 y = 8 \end{matrix}$ ．

(1)、若方程组的解满足x﹣y＝6，求m的值．

(2)、若方程组的解满足x＜﹣y，求满足条件的整数m的最小值．

查看试题解析
21. 如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣3，5），B（﹣2，1），C（﹣1，3）.

（ 1 ）画出△ABC关于x轴的对称图形△A₁B₁C₁.

（ 2 ）画出△A₁B₁C₁沿x轴向右平移4个单位长度后得到的△A₂B₂C₂.

（ 3 ）如果AC上有一点M（a，b）经过上述两次变换，那么对应A₂C₂上的点M₂的坐标是▲.

（ 4 ）△ABC的面积为 ▲.

查看试题解析
22. 消费也扶贫，万源市某村需要销售当地的优质土特产：香米和土豆，这两种商品的相关信息如下表：

商品

香米

土豆

成本（元 $/$ 袋）

60

45

售价（元 $/$ 袋

80

60

(1)、达州市第一中学工会第一季度采购了香米和土豆共计1000袋，为该村创造利润17000元，求达州市第一中学工会采购了香米多少袋？

(2)、为了加大扶贫力度，达州市第一中学工会在第二季度想为该村创造20000元以上利润的目标.该工会计划购进香米和土豆共计1200袋，且香米不低于800袋，不超过1000袋.设购进香米 $m$ 袋，香米和土豆共创造利润 $w$ 元，求出 $w$ 与 $m$ 之间的函数关系式，并通过计算说明达州市第一中学工会能否实现扶贫目标？

查看试题解析
23. 随着春节临近，某儿童游乐场推出了甲、乙两种消费卡，设消费次数为x时，所需费用为y元，且y与x的函数关系如图所示. 根据图中信息，解答下列问题；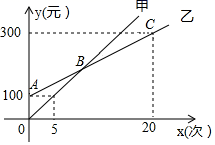

(1)、分别求出选择这两种卡消费时，y关于x的函数表达式.

(2)、求出B点坐标.

(3)、洋洋爸爸准备 $240$ 元钱用于洋洋在该游乐场消费，请问选择哪种消费卡划算？

查看试题解析
24.

(1)、（初步探究）
如图1，在四边形ABCD中， $∠ B = ∠ C = 90 °$ ，点E是边BC上一点， $A B = E C$ ， $B E = C D$ ，连接AE、DE。判断 $△ A E D$ 的形状，并说明理由。

(2)、（解决问题）
如图2，在长方形ABCD中，点P是边CD上一点，在边BC、AD上分别作出点E、F，使得点F、E、P是一个等腰直角三角形的三个顶点，且 $P E = P F$ ， $∠ F P E = 90 °$ ，要求：仅用圆规作图，保留作图痕迹，不写作法。

(3)、（拓展应用）
如图3，在平面直角坐标系xOy中，已知点 $A (2 ， 0)$ ，点 $B (4 ， 1)$ ，点C在第一象限内，若 $△ A B C$ 是等腰直角三角形，则点C的坐标是.

查看试题解析

商品	香米	土豆
成本（元 $/$ 袋）	60	45
售价（元 $/$ 袋	80	60