初中数学人教版一轮复习专题：专题7 一元二次方程

试卷更新日期：2021-12-09 类型：一轮复习

进入出卷网下载

一、单选题

1. 下列方程是关于x的一元二次方程的是（）

A、ax²+bx+c=0 B、x²+ $\frac{1}{x}$ =0 C、2x+c²=0 D、（x﹣2）（3x+1）=x

查看试题解析
2. 把方程 $2 x (x - 1) = 3 x$ 化成一元二次方程的一般形式，则二次项系数、一次项系数、常数项分别是（）

A、 $2 ， 5 ， 0$ B、 $2 ， - 5 ， 0$ C、 $2 ， 5 ， 1$ D、 $2 ， 3 ， 0$

查看试题解析
3. 若（m+2） $x^{m^{2} - 4}$ +3x﹣1＝0是关于x的一元二次方程，则m的值为（）

A、﹣2 B、± C、±2 D、0

查看试题解析
4. $x = 1$ 是关于 $x$ 的一元二次方程 $x^{2} + a x + 2 b = 0$ 的解，则 $2 a + 4 b =$ （）

A、-2 B、-3 C、4 D、-6

查看试题解析
5. 用配方法解方程 $x^{2} + 2 x - 1 = 0$ 时，配方结果正确的是（）

A、 ${(x + 2)}^{2} = 2$ B、 ${(x + 1)}^{2} = 2$ C、 ${(x + 2)}^{2} = 3$ D、 ${(x + 1)}^{2} = 3$

查看试题解析
6. 根据表格估计一元二次方程x²+2x﹣4=0的一个解的范围在（）
x
﹣1
0
1
2
3
x²+2x﹣4
﹣5
﹣4
﹣1
4
11

A、﹣1＜x＜0 B、0＜x＜1 C、1＜x＜2 D、2＜x＜3

查看试题解析
7. 如果关于x的一元二次方程 $k x^{2} - 3 x + 1 = 0$ 有两个实数根，那么 $k$ 的取值范围是（）

A、 $k ⩾ \frac{9}{4}$ B、 $k ⩾ - \frac{9}{4}$ 且 $k \neq 0$ C、 $k ⩽ \frac{9}{4}$ 且 $k \neq 0$ D、 $k ⩽ - \frac{9}{4}$

查看试题解析
8. 已知关于x的方程m²x²+（4m﹣1）x+4=0的两个实数根互为倒数，那么m的值为（　　）

A、2 B、-2 C、±2 D、± $\sqrt{2}$

查看试题解析
9. 肆虐的冠状病毒肺炎具有人传人性，调查发现：1人感染病毒后如果不隔离，那么经过两轮传染将会有225人感染，若设1人平均感染x人，依题意可列方程（）

A、1+x＝225 B、1+x²＝225 C、（1+x）²＝225 D、1+（1+x² ）＝225

查看试题解析
10. 要组织一次篮球比赛，赛制为单循环形式（每两队之间都赛一场），计划安排15场比赛，设应邀请x个球队参加比赛，根据题意可列方程为（）

A、x（x﹣1）=15 B、x（x+1）=15 C、 $\frac{x (x - 1)}{2}$ =15 D、 $\frac{x (x + 1)}{2}$ =15

查看试题解析
11. 如图，在一块长为 $20 m$ ，宽为 $12 m$ 的矩形 $A B C D$ 空地内修建四条宽度相等，且与矩形各边垂直的道路.四条道路围成的中间部分恰好是一个正方形，且边长是道路宽的4倍，道路占地总面积为 $40 m^{2}$ .设道路宽为 $x m$ ，则以下方程正确的是（）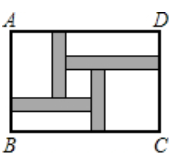

A、 $32 x + 4 x^{2} = 40$ B、 $32 x + 8 x^{2} = 40$ C、 $64 x - 4 x^{2} = 40$ D、 $64 x - 8 x^{2} = 40$

查看试题解析
12. 关于x的一元二次方程 $x^{2} + 2 m x + 2 n = 0$ 有两个整数根且乘积为正，关于y的一元二次方程 $y^{2} + 2 n y + 2 m = 0$ 同样也有两个整数根且乘积为正．给出四个结论：①这两个方程的根都是负根；② ${(m - 1)}^{2} + {(n - 1)}^{2} \geq 2$ ；③ $- 1 \leq 2 m - 2 n \leq 1$ ．其中正确结论的个数是（）

A、0个 B、1个 C、2个 D、3个

查看试题解析

二、填空题

13. 如果 $m$ 、 $n$ 是两个不相等的实数，且满足 $m^{2} - m = 3$ ， $n^{2} - n = 3$ ，那么代数式 $2 n^{2} - m n + 2 m + 2015$ =

查看试题解析
14. 设 $x_{1}$ ， $x_{2}$ 是方程 $2 x^{2} + 3 x - 4 = 0$ 的两个实数根，则 $\frac{1}{x_{1}} + \frac{1}{x_{2}}$ 的值为．

查看试题解析
15. x=时，x²﹣6x+3有最小值，最小值是．

查看试题解析
16. 已知（x²+y²+1）（x²+y²+2）=6，则x²+y²的值为。

查看试题解析
17. 已知方程x²+（a﹣3）x+3＝0在实数范围内恒有解，并且恰有一个解大于1小于2，a的取值范围是．

查看试题解析
18. 某商品原价100元，连续两次涨价后，售价为144元．若平均增长率为x ，则x=。

查看试题解析
19. 对于一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ ，有下列说法：①若 $a + b + c = 0$ ，则 $b^{2} - 4 a c \geq 0$ ；②若方程 $a x^{2} + c = 0$ 有两个不相等的实根，则方程 $a x^{2} + b x + c = 0$ 必有两个不相等的实根；③若 $c$ 是方程 $a x^{2} + b x + c = 0$ 的一个根，则一定有 $a c + b + 1 = 0$ 成立；④若 $x_{0}$ 是一元二次方程 $a x^{2} + b x + c = 0$ 的根，则 $b^{2} - 4 a c = {(2 a x_{0} + b)}^{2}$ ．其中说法正确的有（填序号）．

查看试题解析

三、计算题

20. 解一元二次方程：

(1)、(x+1)²－144=0

(2)、x²－4x－32＝0

(3)、x（x﹣5）=2（x﹣5）

(4)、 $x^{2} - 5 x - 1 = 0$

查看试题解析

四、解答题

21. 某商场购进了一批单价为100元的名牌衬衫，当销售价为150元时，平均每天可售出20件，为了扩大销售、增加盈利，尽快减少库存，商场决定采取适当的降价措施，经调查发现，如果衬衫单价每降价1元，商场平均每天可多售出4件，另外，这批衬衫平均每天要扣除其它成本50元，若商场平均每天盈利2 750元，衬衫单价应定为多少元？

查看试题解析
22. 如图，在一块长为16m，宽为10m的矩形空地中，修建2条同样宽的小路（图中阴影部分），剩下的部分种植草坪，要使草坪的面积为 $135 m^{2}$ ，求道路的宽度.

查看试题解析
23. 已知关于x的一元二次方程x²﹣（3k+1）x+2k²+2k=0
（1）求证：无论k取何实数值，方程总有实数根；
（2）若等腰△ABC的一边长a=6，另两边长b、c恰好是这个方程的两个根，求此三角形的三边长？

查看试题解析

x	﹣1	0	1	2	3
x²+2x﹣4	﹣5	﹣4	﹣1	4	11