2021-2022学年浙教版数学八下第二章一元二次方程优生综合题特训-在线组卷题库

1. 已知正实数x的平方根是m和

m + n

.

(1)、当

n = 6

时，求m的值；

(2)、若

m^{2} x + {(m + n)}^{2} x = 32

，求x的值.

查看试题解析

2. 已知关于x的方程

x^{2} - (m + 2) x + 2 m - 1 = 0

(1)、求证：无论m为任何数，此方程总有两个不相等的实数根.

(2)、若此方程的一个根是1，请求出m的值和方程的另一个根，并求出以此两根为边长的直角三角形的周长.

查看试题解析

3. 为缅怀革命英烈、传承红色基因，在今年“五一”小长假期间，各地游客纷纷来到重庆歌乐山烈士陵园瞻仰革命遗址.据统计，重庆歌乐山烈士陵园4月30日接待游客1.2万人次，5月2日接待游客2.7万人次.

(1)、求今年4月30日到5月2日，重庆歌乐山烈士陵园接待游客的日平均增长率；

(2)、由于暴雨天气，重庆歌乐山烈士陵园5月3日接待游客人次比5月2日减少了

\frac{1}{3}

，5月4日天气放晴，接待游客人次比5月3日增加了6a%，又因假期即将结束，5月5日接待游客人次比5月4日减少了

\frac{15}{4}

a%，即使这样，5月5日接待游客人次还是比4月30日增加了50%，求a的值.

查看试题解析

4. 苏州某工厂生产一批小家电，2019年的出厂价是144元，2020年、2021年连续两年改进技术降低成本，2021年出厂价调整为100元.

(1)、这两年出厂价下降的百分比相同，求平均下降的百分率（精确到0.01%）.

(2)、某商场今年销售这批小家电的售价为140元时，平均每天可销售20台，为了减少库存，商场决定降价销售，经调查发现小家电单价每降低5元，每天可多售出10台，如果每天盈利1250元，销售单价应为多少元？

查看试题解析

5.

(1)、用配方法解一元二次方程除了课本的方法，也可以用下面的配方方式：

将 $a x^{2} + b x + c = 0 (a \neq 0)$ 两边同时乘以 $4 a$ 并移项，得到 $4 a^{2} x^{2} + 4 a b x = - 4 a c$ ，两边再同时加上 $b^{2}$ ，得（ ▲ ）² $= b^{2} - 4 a c$ .请用这样的方法解方程： $3 x^{2} + 5 x + 1 = 0$ ；

(2)、华裔数学家罗博深在2019年提出了一种全新的一元二次方程解法，对于

x^{2} + b x + c = 0

，将等式左边进行因式分解，得到以下形式：

$x^{2} + b x + c = (x - m) \cdot (x - n)$ （从这里可以看出方程的解为 $x_{1} = m$ ， $x_{2} = n$ ）

即 $x^{2} + b x + c = x^{2} - (m + n) x + m n$

因为 $m + n = - b$ ，所以 $m$ 、 $n$ 的平均数为 $- \frac{b}{2}$ ，不妨设 $m = - \frac{b}{2} + p$ ， $n = - \frac{b}{2} - p$ ，

利用 $x_{1} \cdot x_{2} = m n$ ，得 $(- \frac{b}{2} + p) \cdot (- \frac{b}{2} - p) = c$ ，所以 ${(- \frac{b}{2})}^{2} - p^{2} = c$ ，即能求出 $p$ 的值.

举例如下：解一元二次方程 $x^{2} - 2 x - 4 = 0$ ，由于 $- \frac{b}{2} = 1$ ，所以方程的两个根为 $1 \pm p$ ，而 $1^{2} - p^{2} = - 4$ ，解得 $p = \pm \sqrt{5}$ ，所以方程的解为 $x_{1} = 1 + \sqrt{5}$ ， $x_{2} = 1 - \sqrt{5}$ .

请运用以上方法解如下方程① $x^{2} - 2 \sqrt{3} x - 4 = 0$ ；② $3 x^{2} - \sqrt{11} x + \frac{1}{2} = 0$

查看试题解析

6. 用总长700cm的木板制作矩形置物架ABCD (如图)，已知该置物架上面部分为正方形ABFE，下面部分是两个全等的矩形DGMN和矩形CNMH，中间部分为矩形EFHG。已知DG=60cm，设正方形的边长AB=x (cm)。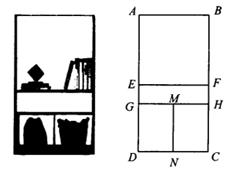

(1)、当x=75时，EG的长为cm

(2)、置物架ABCD的高AD的长为cm (用含x的代数式表示)

(3)、为了便于置放物品，EG的高度不小于26cm，若矩形ABCD的面积为12750 (cm²)，求x的值。

查看试题解析

7. 随着“共享经济”的概念迅速普及，共享汽车也进入了人们的视野．某共享汽车租赁公司年初在某地投放了一批共享汽车，全天包车的租金定为每辆120元．据统计，三月份的全天包车数为25次，在租金不变的基础上，四、五月的全天包车数持续走高，五月份的全天包车数达到64次.

(1)、若从三月份到五月份的全天包车数月平均增长率不变，求全天包车数的月平均增长率；

(2)、从六月份起，该公司决定降低租金，经调查发现，租金每降价a元，全天包车数增加1.6a次，当租金降价多少元时，公司将获利8800元？

查看试题解析

8. 某租赁公司有房屋

100

套.据统计，当每套房屋的月租金为

3000

元时，可全部租出.每套房屋的月租金每增加

50

元，租出的房屋数将减少

1

套.

(1)、当每套房屋的月租金定为

3500

元时，能租出多少套？

(2)、当每套房屋的月租金定价为多少元时，租赁公司的月租金可达到

315000

元？

查看试题解析

9. 已知关于x的一元二次方程

x^{2} - 4 m x + 4 m^{2} - 9 = 0

.

(1)、求证：此方程有两个不相等的实数根；

(2)、设此方程的两个根分别为

x_{1}

，

x_{2}

，若

\frac{1}{2} x_{1} = 3 - \frac{1}{2} x_{2}

，求方程的两个根.

查看试题解析

10. 已知关于

x

的一元二次方程

x^{2} - (2 m - 2) x + (m^{2} - 2 m) = 0

.

(1)、求证：方程有两个不相等的实数根；

(2)、如果方程的两个实数根为

x_{1}

，

x_{2}

，且

x_{1} + x_{2} + x_{1} x_{2} = 10

，求

m

的值.

查看试题解析

11. 已知x₁ ， x₂是关于x的一元二次方程x²﹣4x+m＝0的两个实数根．

(1)、求m的取值范围；

(2)、若x₁+x₂﹣x₁x₂＝1，计算m的值．

查看试题解析

12. 已知关于

x

的一元二次方程

x^{2} - 2 x + k + 2 = 0

.

(1)、若

k = - 6

，求此方程的解；

(2)、若该方程无实数根，求

k

的取值范围.

查看试题解析

13. 已知关于

x

的方程

x^{2} - 4 m x + 4 m^{2} - 9 = 0

.

(1)、求证：该方程有两个不相等的实数根；

(2)、若该方程有一个根-1，求

m

的值.

查看试题解析

14. 学校为了美化校园环境，在一块长40米，宽20米的长方形空地上计划新建一块长9米，宽7米的长方形花圃.

(1)、若请你在这块空地上设计一个长方形花圃，使它的面积比学校计划新建的长方形花圃的面积多1平方米，请你给出你认为合适的三种不同的方案；

(2)、在学校计划新建的长方形花圃周长不变的情况下，长方形花圃的面积能否增加2平方米？如果能，请求出长方形花圃的长和宽；如果不能，请说明理由.

查看试题解析

15. 已知点

P (1 ， m)

、

Q (n ， 1)

在反比例函数

y = \frac{5}{x}

的图象上，直线

y = k x + b

经过点

P

、

Q

，且与

x

轴、

y

轴的交点分别为

A

、

B

两点．

(1)、求直线

P Q

的解析式；

(2)、

O

为坐标原点，点

D

在直线上（点

C

与点

B

不重合），

A B = A C

，求点

C

的坐标；

(3)、在（2）的条件下，点

D

在坐标平面上，顺次联结点

O

、

B

、

C

、

D

的四边形

O B C D

满足：

B C // O D

，

B O = C D

，求满足条件的点

D

坐标．

查看试题解析

16. 某村2018年的人均收入为30000元，2020年的人均收入为36300元．

(1)、求2018年到2020年该村人均收入的年平均增长率；

(2)、假设2021年该村人均收入的增长率与前两年的年平均增长率相同，请你预测2021年该村的人均收入是多少元？

查看试题解析

17. 青山村种的水稻2010年平均每公顷产7200kg，2012年平均每公顷产8712kg．

(1)、求水稻每公顷产量的年平均增长率；

(2)、2010年水稻平均每千克的成本为2元，每千克的售价为3元，2011年水稻平均每千克的成本比2010年的增加了10%，若2011年平均每公顷水稻的利润比2010年至少增加720元，则2011年平均每千克水稻的售价最少应为多少元?

查看试题解析

18. 为落实国务院房地产调控政策，使“居者有其屋”，某市加快了廉租房的建设力度.2019年市政府共投资2亿元人民币建设了廉租房8万平方米，预计到2021年底三年累计投资9.5亿元人民币建设廉租房，若在这两年内每年投资的增长率相同.

(1)、求每年市政府投资的增长率；

(2)、若这两年内的建设成本不变，求到2021年底共建设了多少万平方米的廉租房？

查看试题解析

19. 为了丰富市民的文化生活，我市某景点开放夜游项目．为吸引游客组团来此夜游，特推出了如下门票收费标准：

标准一：如果人数不超过20人，门票价格为60元/人；

标准二：如果人数超过20人，每超过1人，门票价格降低2元，但门票价格不低于50元/人．

(1)、当夜游人数为15人时，人均门票价格为元；当夜游人数为25人时，人均门票价格为元；

(2)、若某单位支付门票费用共1232元，则该单位这次共有多少名员工去此景点夜游？

查看试题解析

20. 科学研究表明接种疫苗是战胜新冠病毒的最有效途径.当前居民接种疫苗迎来高峰期，导致相应医疗物资匮乏，某工厂及时补进了一条一次性注射器生产线生产一次性注射器.开工第一天生产200万个，第三天生产288万个.试回答下列问题：

(1)、求前三天生产量的日平均增长率；

(2)、经调查发现，1条生产线最大产能是600万个/天，若每增加

1

条生产线，每条生产线的最大产能将减少20万个/天.

①现该厂要保证每天生产一次性注射2600万个，在增加产能同时又要节省投入的条件下（生产线越多，投入越大），应该增加几条生产线？

②是否能增加生产线，使得每天生产一次性注射器5000万个，若能，应该增加几条生产线？若不能，请说明理由.

查看试题解析

21. 某汽车销售公司6月份销售某厂家的汽车，在一定范围内，每部汽车的进价与销售有如下关系，若当月仅售出1部汽车，则该部汽车的进价为27万元，每多售一部，所有出售的汽车的进价均降低0.1万元/部．月底厂家根据销售量一次性返利给销售公司，销售量在10部以内，含10部，每部返利0.5万元，销售量在10部以上，每部返利1万元．

(1)、若该公司当月卖出3部汽车，求每部汽车的进价是多少万元；

(2)、如果汽车的销售价位28万元/部，该公司计划当月盈利12万元，那么要卖出

多少部汽车？（盈利＝销售利润＋返利）

查看试题解析

22. 解答下列各题：

(1)、用配方法解方程：x²+12x=-9

(2)、设x₁ ， x₂是一元二次方程5x²-9x-2=0的两根，求