山东省青岛市崂山区2021-2022学年七年级上学期期中数学试题
试卷更新日期:2021-12-08 类型:期中考试
一、单选题
-
1. 将所给图形绕虚线旋转一周,能形成的几何体是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 的倒数是( )A、 B、 C、 D、3. 下列式子中,正确的是( )A、 B、 C、 D、4. 下列不是正方体表面展开图的是( )A、
2. 的倒数是( )A、 B、 C、 D、3. 下列式子中,正确的是( )A、 B、 C、 D、4. 下列不是正方体表面展开图的是( )A、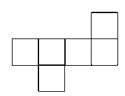 B、
B、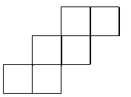 C、
C、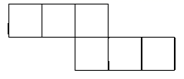 D、
D、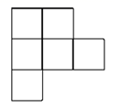 5. 如图,数轴上点A,B分别对应有理数a,b,则下列结论正确的是( )
5. 如图,数轴上点A,B分别对应有理数a,b,则下列结论正确的是( ) A、a>b B、|a|>|b| C、a+b>0 D、﹣a>b6. 我国森林覆盖面积约为1340000平方千米,这个数字用科学记数法表示为( )A、 B、 C、 D、7. 下列说法中,正确的是( )A、 的系数是 B、单项式 的次数是2,系数为 C、 的次数是8 D、 是单项式8. 将一组正整数按如图所示的规律排列下去,若有序数对 表示第 行,从左到右第 个数,如 表示的数为8,则正整数2021可以用下列哪一个有序数对来表示( )
A、a>b B、|a|>|b| C、a+b>0 D、﹣a>b6. 我国森林覆盖面积约为1340000平方千米,这个数字用科学记数法表示为( )A、 B、 C、 D、7. 下列说法中,正确的是( )A、 的系数是 B、单项式 的次数是2,系数为 C、 的次数是8 D、 是单项式8. 将一组正整数按如图所示的规律排列下去,若有序数对 表示第 行,从左到右第 个数,如 表示的数为8,则正整数2021可以用下列哪一个有序数对来表示( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 下列数: ,其中负数有个。10. 如果一个棱柱由八个面围成,那么这个棱柱是棱柱.11. 如图是正方体的一种展开图,其中每个面上都有一个数字,在原正方体中,与数字1相对面上的数字是。
 12. 若 与 是同类项,则 .13. 若 ,则 .14. 已知代数式 的值是6,则代数式 的值为。15. 对于任意有理数 、 ,定义一种新运算“ ”,规则如下: ,例如: ,则 .16. 观察下列等式: , , , , , ,…,根据其中的规律可得 的结果的个位数字是 .
12. 若 与 是同类项,则 .13. 若 ,则 .14. 已知代数式 的值是6,则代数式 的值为。15. 对于任意有理数 、 ,定义一种新运算“ ”,规则如下: ,例如: ,则 .16. 观察下列等式: , , , , , ,…,根据其中的规律可得 的结果的个位数字是 .三、解答题
-
17. 如图是由若干块小正方体积木堆成的几何体请分别画出从正面、左面、上面所看到的几何体的形状图.
 18. 计算:(1)、 ;(2)、(3)、(4)、19. 化简:(1)、 ;(2)、 .(3)、先化简再求值: ,其中 , .20. 2020年的“新冠肺炎”疫情的蔓延,使得医用口罩销量大幅增加,某口罩加工厂为满足市场需求计划每天生产5000个,由于各种原因实际每天生产量相比有出入,表格是二月份某一周的生产情况(超产为正,减产为负,单位:个).
18. 计算:(1)、 ;(2)、(3)、(4)、19. 化简:(1)、 ;(2)、 .(3)、先化简再求值: ,其中 , .20. 2020年的“新冠肺炎”疫情的蔓延,使得医用口罩销量大幅增加,某口罩加工厂为满足市场需求计划每天生产5000个,由于各种原因实际每天生产量相比有出入,表格是二月份某一周的生产情况(超产为正,减产为负,单位:个).星期
一
二
三
四
五
六
日
增减
+100
-200
+400
-100
-100
+350
+150
(1)、根据记录可知前三天共生产多少个口罩;(2)、产量最多的一天比产量最少的一天多生产多少个;(3)、该口罩加工厂实行计件工资制,每生产一个口罩0.2元,本周口罩加工厂应支付工人的工资总额是多少元?21. 苏宁电器销售两种电器A和B,电器A每台定价800元,电器B每台定价200元.双十一期间商场促销,向客户提供两种优惠方案.方案一:买一台A送一台B;
方案二:电器A和电器B都按定价的90%付款.现某客户要到该卖场购买电器A10台,电器B x台(x>10).
(1)、若该客户按方案一购买,需付款元;(用含x的代数式表示)若该客户按方案二购买,需付款元.(用含x的代数式表示)(2)、若x=30,通过计算说明此时按哪种方案购买较为合算?22. 将图1中的正方形剪开得到图2,则图2中共有4个正方形;将图2中的一个正方形剪开得到图3,图3中共有7个正方形;将图3中4个较小的正方中的一个剪开得到图4,则图4中共有10个正方形,照这个规律剪下去…… (1)、根据图中的规律补全下表:
(1)、根据图中的规律补全下表:图形标号
1
2
3
4
5
6
…
n
正方形个数
1
4
7
10
…
(2)、求第几幅图形中有2020个正方形?23. 如图 (1)、问题提出:如果从1,2,3…… , 个连续的自然数中选择 个连续的自然数( ),有多少种不同的选择方法?(2)、问题探究:
(1)、问题提出:如果从1,2,3…… , 个连续的自然数中选择 个连续的自然数( ),有多少种不同的选择方法?(2)、问题探究:为发现规律,我们采用一般问题特殊化的策略,先从最简单的问题入手,再逐次递进,最后得出一般性的结论.
①探究一:
如果从1,2,3…… , 个连续的自然数中选择2个连续的自然数,会有多少种不同的选择方法?
如图1,当 , 时,显然有2种不同的选择方法;
如图2,当 , 时,有1,2;2,3;3,4这3种不同的选择方法;
如图3,当 , 时,有4种不同的选择方法;……
由上可知:从 个连续的自然数中选择2个连续的自然数,有种不同的选择方法.
②探究二:
如果从1,2,3……100,100个连续的自然数中选择3个,4个…… 个连续的自然数,分别有多少种不同的选择方法?
我们借助下面的框图继续探究,发现规律并应用规律完成填空
1
2
3
…
93
94
95
96
97
98
99
100
从100个连续的自然数中选择3个连续的自然数,有98种不同的选择方法;
从100个连续的自然数中选择4个连续的自然数,有97种不同的选择方法;……
从100个连续的自然数中选择8个连续的自然数,有93种不同的选择方法;……
由上可知:如果从1,2,3……100,100个连续的自然数中选择 个连续的自然数,有种不同的选择方法.
(3)、问题解决:如果从1,2,3…… , 个连续的自然数中选择 个连续的自然数( ),有种不同的选择方法.24. 阅读下面材料:点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为|AB|.当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a﹣b|;当A、B两点都不在原点时,
①如图2,点A、B都在原点的右边|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|;
②如图3,点A、B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=|a﹣b|;
③如图4,点A、B在原点的两边,|AB|=|OB|+|OA|=|a|+|b|=a+(﹣b)=|a﹣b|

回答下列问题:
(1)、数轴上表示2和5的两点之间的距离是 , 数轴上表示﹣2和﹣5的两点之间的距离是 , 数轴上表示1和﹣3的两点之间的距离是;(2)、数轴上表示x和﹣1的两点A和B之间的距离是 , 如果|AB|=2,那么x为;(3)、代数式|x+1|+|x﹣2|取最小值时,相应的整数x的取值是 .