山东省济南市槐荫区2021-2022学年七年级上学期期中数学试题
试卷更新日期:2021-12-08 类型:期中考试
一、单选题
-
1. 的相反数为( )A、 B、2021 C、 D、2. 检测4个排球,其中超过标准的克数记为正数,低于标准的克数记为负数,从轻重的角度来看,最接近标准的球是( )A、
 B、
B、 C、
C、 D、
D、 3. 2021年9月20日“天舟三号”在海南成功发射,这是中国航天工程又一重大突破,它的运行轨道距离地球393 000米,数据393 000米用科学记数法表示为( )A、 米 B、 米 C、 米 D、 米4. 下列说法正确的是( )A、单项式 的系数是1 B、单项式 的次数是3 C、 不是整式 D、 是四次三项式5. 如图,用一个平面去截圆锥,得到的截面是( )
3. 2021年9月20日“天舟三号”在海南成功发射,这是中国航天工程又一重大突破,它的运行轨道距离地球393 000米,数据393 000米用科学记数法表示为( )A、 米 B、 米 C、 米 D、 米4. 下列说法正确的是( )A、单项式 的系数是1 B、单项式 的次数是3 C、 不是整式 D、 是四次三项式5. 如图,用一个平面去截圆锥,得到的截面是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 下列说法中,错误的是( )A、数轴上表示 的点距离原点3个单位长度 B、规定了原点、正方向和单位长度的直线叫做数轴 C、有理数0在数轴上表示的点是原点 D、表示十万分之一的点在数轴上不存在7. 如图是一个几何体的俯视图,则该几何体是( )
6. 下列说法中,错误的是( )A、数轴上表示 的点距离原点3个单位长度 B、规定了原点、正方向和单位长度的直线叫做数轴 C、有理数0在数轴上表示的点是原点 D、表示十万分之一的点在数轴上不存在7. 如图是一个几何体的俯视图,则该几何体是( ) A、
A、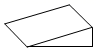 B、
B、 C、
C、 D、
D、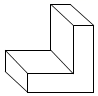 8. 在代数式 , , , , , 中,整式有( )A、3个 B、4个 C、5个 D、6个9. 把 写成省略加号和的形式( )A、 B、 C、 D、10. 计算 的结果是A、 B、 C、 D、11. 已知 , ,且 .则 的值为( )A、 B、 C、 或 D、 或12. 某路公交车从起点经过 , , , 站到达终点,各站上、下乘客人数如下表所示(用正数表示上车的人数,负数表示下车的人数)
8. 在代数式 , , , , , 中,整式有( )A、3个 B、4个 C、5个 D、6个9. 把 写成省略加号和的形式( )A、 B、 C、 D、10. 计算 的结果是A、 B、 C、 D、11. 已知 , ,且 .则 的值为( )A、 B、 C、 或 D、 或12. 某路公交车从起点经过 , , , 站到达终点,各站上、下乘客人数如下表所示(用正数表示上车的人数,负数表示下车的人数)站点
起点
终点
上车人数
15
12
7
5
0
下车人数
0
若此公交车采用一票制,即每位上车乘客无论哪站下车,车票都是2元,问该车这次出车共收入( )
A、114元 B、228元 C、78元 D、56元二、填空题
-
13. 《九章算术》中注有“今两算得失相反,要令正负以名之”.大意是:今有两数若其意义相反,则分别叫做正数与负数.若水位上升2m记作 m,则下降1m记作m.14. 电视剧《西游记》中,孙悟空的“金箍棒”飞速旋转,形成一个圆面,这说明(请填入符合题意答案的序号).
①点动成线;②线动成面;③面动成体.
15. 已知正方体的一个平面展开图如图所示,则在原正方体上“百”的对面是 . 16. 在国家房贷政策调控下,某楼盘为促销打算降价销售,原价 元 平方米的楼房,按八五折销售,小张购买该楼盘100平方米的房子比原来节省了元.17. 有理数 、 在数轴上的位置如图所示,则下列各式:
16. 在国家房贷政策调控下,某楼盘为促销打算降价销售,原价 元 平方米的楼房,按八五折销售,小张购买该楼盘100平方米的房子比原来节省了元.17. 有理数 、 在数轴上的位置如图所示,则下列各式:① ;② ;③ ;④ ;⑤ ,
正确的有 . (填式子前面的序号即可)
 18. 有一种密码,将英文26个字母 、 、 、…、 (不论大小写)依次对应1、2、3、…、26,这26个自然数(见表格),当明码对应的序号 为奇数时,密码对应的序号为 ,当明码对应的序号 偶数时,密码对应的序号为 ,按上述规定,将明码“ ”译成密码是 .
18. 有一种密码,将英文26个字母 、 、 、…、 (不论大小写)依次对应1、2、3、…、26,这26个自然数(见表格),当明码对应的序号 为奇数时,密码对应的序号为 ,当明码对应的序号 偶数时,密码对应的序号为 ,按上述规定,将明码“ ”译成密码是 .字母
序号
1
2
3
4
5
6
7
8
9
10
11
12
13
字母
序号
14
15
16
17
18
19
20
21
22
23
24
25
26
19. 如图,数轴上点A表示的有理数为﹣4,点B表示的有理数为6,点P从点A出发以每秒2个单位长度的速度在数轴上沿由A到B方向运动,当点P到达点B后立即返回,仍然以每秒2个单位长度的速度点运动至点A停止运动,设运动时间为t(单位:秒). (1)、当t=2时,点P表示的有理数为 .(2)、当点P与点B重合时t的值为 .(3)、①在点P由A到点B的运动过程中,点P与点A的距离为 . (用含t的代数式表示)
(1)、当t=2时,点P表示的有理数为 .(2)、当点P与点B重合时t的值为 .(3)、①在点P由A到点B的运动过程中,点P与点A的距离为 . (用含t的代数式表示)②在点P由点A到点B的运动过程中,点P表示的有理数为 . (用含t的代数式表示)
(4)、当点P表示的有理数与原点距离是2的单位长度时,t的值为 .三、解答题
-
20. 计算:(1)、 ;(2)、 .21. 计算:22. 计算: .23. 如图,上面的图形分别是下面哪个立体图形展开的形状,请你把有对应关系的平面图形与立体图形连接起来.
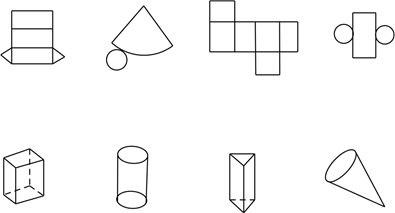 24. 某服装厂生产一种西装和领带,西装每套定价200元,领带每条定价40元.厂方在开展促销活动期间,向客户提供两种优惠方案:
24. 某服装厂生产一种西装和领带,西装每套定价200元,领带每条定价40元.厂方在开展促销活动期间,向客户提供两种优惠方案:①买一套西装送一条领带;
②西装和领带都按定价的90%付款.
现某客户要到该服装厂购买西装20套,领带x条(x>20).
(1)、若该客户按方案①购买,需付款元(用含x的代数式表示);若该客户按方案②购买,需付款元(用含x的代数式表示);
(2)、若x=30,通过计算说明此时按哪种方案购买较为合算?25. 阅读材料:对于 可以如下计算:原式
.
上面这种方法叫拆数法,仿照上面的方法,请你计算:
.
26.(1)、例:代数式 表示 、 两数和的平方,仿照上例填空:代数式 表示(2)、试计算 、 取不同数值时, 及 的值,填入表:、 的值
当 , 时
当 , 时
当 , 时
(3)、我的发现:;(4)、用你发现的规律计算: .27. 科技改变生活,当前网络销售日益盛行,许多农商采用网上销售的方式进行营销,实现脱贫致富.小王把自家种的柚子放到网上销售,计划每天销售100千克,但实际每天的销售量与计划销售量相比有增减,超过计划量记为正,不足计划量记为负.下表是小王第一周柚子的销售情况:星期
一
二
三
四
五
六
日
柚子销售超过或不足计划量情况(单位:千克)
(1)、小王第一周销售柚子最多的一天比最少的一天多销售多少千克?(2)、小王第一周实际销售柚子的总量是多少千克?(3)、若小王按8元 千克进行柚子销售,平均运费为3元 千克,则小王第一周销售柚子一共收入多少元?