辽宁省沈阳市大东区2021-2022学年七年级上学期期中数学试题
试卷更新日期:2021-12-08 类型:期中考试
一、单选题
-
1. ﹣7的相反数是( )A、﹣7 B、 C、7 D、12. 中国幅员辽阔,陆地面积约为960万平方公里,“960万”用科学记数法表示为( )A、0.96×107 B、9.6×106 C、96×105 D、9.6×1023. 下列各图中,经过折叠能围成一个正方体的是( )A、
 B、
B、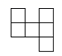 C、
C、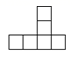 D、
D、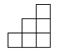 4. 实数a,b,c,d在数轴上的对应点的位置如图所示,则正确的结论是( )
4. 实数a,b,c,d在数轴上的对应点的位置如图所示,则正确的结论是( )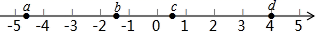 A、a>﹣4 B、bd>0 C、|a|>|d| D、b+c>05. 在﹣0.1428中用数字3替换其中的一个非0数码后,使所得的数最大,则被替换的字是( )A、1 B、2 C、4 D、86. 下列说法正确的是( )A、 不是整式 B、﹣2x2y与y2x是同类项 C、y是单项式 D、﹣3x2y的次数是47. 当x=2时,代数式ax3+bx+1的值为6,那么当x=﹣2时,这个代数式的值是( )A、1 B、﹣4 C、6 D、﹣58. 如图,下列说法错误的是( )
A、a>﹣4 B、bd>0 C、|a|>|d| D、b+c>05. 在﹣0.1428中用数字3替换其中的一个非0数码后,使所得的数最大,则被替换的字是( )A、1 B、2 C、4 D、86. 下列说法正确的是( )A、 不是整式 B、﹣2x2y与y2x是同类项 C、y是单项式 D、﹣3x2y的次数是47. 当x=2时,代数式ax3+bx+1的值为6,那么当x=﹣2时,这个代数式的值是( )A、1 B、﹣4 C、6 D、﹣58. 如图,下列说法错误的是( ) A、 是一个平角 B、 也可以表示为 C、 也可以表示为 D、 也可以表示为9. 已知∠AOB=30°,∠BOC=45°,则∠AOC等于( )A、15° B、75° C、15°或75° D、不能确定10. 下列说法正确的有( )
A、 是一个平角 B、 也可以表示为 C、 也可以表示为 D、 也可以表示为9. 已知∠AOB=30°,∠BOC=45°,则∠AOC等于( )A、15° B、75° C、15°或75° D、不能确定10. 下列说法正确的有( )①n棱柱有2n个顶点,2n条棱,(n+2)个面(n为不小于3的正整数);②点动成线,线动成面,面动成体;③圆锥的侧面展开图是一个圆;④用平面去截一个正方体,截面的形状可以是三角形、四边形、五边形、六边形.
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 在我校第8届校运会的跳远比赛中,以4.00米为标准,若小明跳出了4.22米,可记做+0.22,那么小东跳出了3.85米,记作 .12. 如果圆柱的侧面展开图是相邻两边长分别为6,16π的长方形,那么这个圆柱的体积等于13. 第一节课是上午7:50上课,8:35下课,这节课期间时针转过的角度为(用度分秒的形式表示)14. 如图定义一种新运算“⊗”,如:2⊗1= =2;x⊗y= ,则(4⊗2)⊗(﹣1)= .15. 如图所示的运算程序中,皆开始输入x的值为48,第一次输出的结果是24,第二次输出的结果是12,第三次输出的结果是6,……则第2021次输出的结果为 .
 16. 已知关于x,y的代数式ax2+2x+x2﹣3y2﹣bx+4y﹣5的值与x的取值无关,则a﹣b= .
16. 已知关于x,y的代数式ax2+2x+x2﹣3y2﹣bx+4y﹣5的值与x的取值无关,则a﹣b= .三、解答题
-
17. 计算:(1)、 ;(2)、 .18. 先化简,再求值: ,其中 .19. 在方格中依次画出从正面、左面、上面看到的如图所示几何体的形状图.
 20. 如图,已知四点A,B,C,D,请用直尺按要求完成作图.
20. 如图,已知四点A,B,C,D,请用直尺按要求完成作图.( 1 )作射线AD;
( 2 )作直线BC;
( 3 )连接BD,请在BD上确定点P,使AP+CP的值最小,并说明理由.
 21. 一辆货车从货场 出发,向东走2千米到达批发部 ,继续向东走1.5千米到达商场 ,又向西走5.5千米到达超市 ,最后回到货场.(1)、以货场为原点,以东为正方向,用一个单位长度表示1千米,你能在数轴上分别表示出货场 ,批发部 ,商场 ,超市 的位置吗?(2)、超市 距离货场 多远?(3)、此货车每千米耗油0.1升,每升汽油6.20元,请计算此货车一共需要多少汽油费?22. 将7张相同的小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好被分割为两个长方形,面积分别为S1 , S2 , 已知小长方形纸片的长为a,宽为b,且a>b
21. 一辆货车从货场 出发,向东走2千米到达批发部 ,继续向东走1.5千米到达商场 ,又向西走5.5千米到达超市 ,最后回到货场.(1)、以货场为原点,以东为正方向,用一个单位长度表示1千米,你能在数轴上分别表示出货场 ,批发部 ,商场 ,超市 的位置吗?(2)、超市 距离货场 多远?(3)、此货车每千米耗油0.1升,每升汽油6.20元,请计算此货车一共需要多少汽油费?22. 将7张相同的小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好被分割为两个长方形,面积分别为S1 , S2 , 已知小长方形纸片的长为a,宽为b,且a>b (1)、当a=9,b=2,AD=30时,请求:
(1)、当a=9,b=2,AD=30时,请求:①长方形ABCD的面积;
②S2﹣S1的值.
(2)、当AD=30时,请用含a,b的式子表示S2﹣S1的值.23. 观察下列等式,探究其中的规律并解答问题:1=12
2+3+4=32
3+4+5+6+7=52
4+5+6+7+8+9+10=k2
(1)、第4个等式中,k=;(2)、写出第s个等式:;(3)、写出第n个等式:(其中n为正整数)24. 如图1,直线DE上有一点O,过点O在直线DE上方作射线OC,将一直角三角板AOB(其中∠OAB=30°)的直角顶点放在点O处,一条直角边OA在射线OD上,另一边OB在直线DE上方,将直角三角板绕着点O按每秒10°的速度逆时针旋转一周,设旋转时间为t秒. (1)、当直角三角板旋转到如图2的位置时,OA恰好平分∠COD,此时,∠BOC与∠BOE之间有何数量关系 ;(2)、若射线OC的位值保持不变,且∠COE=140°
(1)、当直角三角板旋转到如图2的位置时,OA恰好平分∠COD,此时,∠BOC与∠BOE之间有何数量关系 ;(2)、若射线OC的位值保持不变,且∠COE=140°①在旋转的过程中,是否存在某个时刻,使得射线OA,OC,OD中的某一条射线是另两条射线所夹角的角平分线?若存在,请直接写出所有满足题意t的取值 ,若不存在,请说明理由;
②在旋转的过程中,当边AB与射线OE相交时,如图3,请直接写出∠AOC﹣∠BOE的值 .
25. 点O为数轴的原点,点A、B在数轴上的位置如图所示,点A表示的数为5,线段AB的长为线段OA长的1.2倍.点C在数轴上,M为线段OC的中点 (1)、点B表示的数为(2)、若线段BM的长为4.5,则线段AC的长为(3)、若线段AC的长为x,求线段BM的长(用含x的式子表示)
(1)、点B表示的数为(2)、若线段BM的长为4.5,则线段AC的长为(3)、若线段AC的长为x,求线段BM的长(用含x的式子表示)