江西省宜春市高安市2021-2022学年七年级上学期期中数学试题

试卷更新日期：2021-12-08 类型：期中考试

进入出卷网下载

一、单选题

1. -2的倒数是（）

A、-2 B、 $- \frac{1}{2}$ C、 $\frac{1}{2}$ D、2

查看试题解析
2. 若|x|＝5，|y|＝2且x＜0，y＞0，则x+y＝（）

A、7 B、﹣7 C、3 D、﹣3

查看试题解析
3. 下列代数式符合书写要求的是（）

A、7 $\frac{1}{2}$ xy B、ab×9 C、 $\frac{x y^{3}}{5}$ D、1÷a

查看试题解析
4. 已知代数式x²﹣x+1的值为9，则3x²﹣3x﹣1的值为（）

A、23 B、﹣26 C、﹣23 D、26

查看试题解析
5. 六张形状大小完全相同的小长方形（白色部分）如图摆放在大长方形 $A B C D$ 中， $B C = n$ ， $A B = m$ ，则图中两块阴影部分长方形的周长和是（）．

A、 $4 m$ B、 $4 n$ C、 $2 (m + n)$ D、 $4 (m - n)$

查看试题解析
6. 如图，是一个运算程序的示意图，若开始输入x的值为3125，则第2021次输出的结果为（）

A、1 B、5 C、25 D、625

查看试题解析

二、填空题

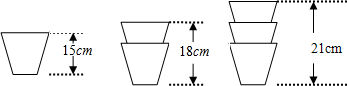
7. 《福建省新冠病毒疫苗接种工作方案》指出：经测算，人群接种率需达到77.6%以上，才能建立免疫屏障，福建省需完成约6000万剂次（每人接种2剂次）的疫苗接种．数据60000000用科学记数法表示为．

查看试题解析
8. 已知关于 $x ， y$ 的多项式 $m x^{2} + 4 x y - 7 x - 3 x^{2} + 2 n x y - 5 y$ 合并后不含有二次项，则 $n^{m} =$ ．

查看试题解析
9. x，y表示两个数，规定新运算“※”及“△”如下：x※y=6x+5y，x△y=3xy，则（﹣2※3）△（﹣4）= ．

查看试题解析
10. 若单项式 $- \frac{1}{3} x^{2 m - 3} y^{4}$ 与 $3 x^{5} y^{n + 2}$ 的和仍是单项式，则 $m n =$ ．

查看试题解析
11. 某种杯子的高度是15cm，两个以及三个这样的杯子叠放时高度如图，n个这样的杯子叠放在一起高度是cm（用含n的式子表示）．

查看试题解析
12. 对于正数 $x$ ，规定 $f (x) = \frac{x}{1 + x}$ ，例如： $f (2) = \frac{2}{1 + 2} = \frac{2}{3}$ ， $f (3) = \frac{3}{1 + 3} = \frac{3}{4}$ ， $f (\frac{1}{2}) = \frac{\frac{1}{2}}{1 + \frac{1}{2}} = \frac{1}{3}$ ， $f (\frac{1}{3}) = \frac{\frac{1}{3}}{1 + \frac{1}{3}} = \frac{1}{4}$ ……利用以上规律计算：
$f (\frac{1}{2019}) + f (\frac{1}{2018}) + f (\frac{1}{2017}) + \cdot \cdot \cdot \cdot \cdot \cdot + f (\frac{1}{3}) + f (\frac{1}{2})$ $+ f (1) + f (2) + \cdot \cdot \cdot \cdot \cdot \cdot + f (2019)$ 的值为：.

查看试题解析

三、解答题

13. 计算：

(1)、（ $\frac{1}{2} - \frac{2}{3} - \frac{5}{6}$ ）×（﹣60）；

(2)、 $- 1^{6} + 2 \times {(- 3)}^{2} - 5 \div \frac{1}{2} \times 2$ ．

查看试题解析
14. 已知a，b互为倒数，c，d互为相反数，m为最大的负整数.试求 $\frac{m}{3} + a b + \frac{c + d}{4 m}$ 的值.

查看试题解析
15. 先化简，再求值： $5 (3 a^{2} b - a b^{2}) - 4 (- a b^{2} + 3 a^{2} b)$ .其中 $a = \frac{1}{2}, b = - 4$

查看试题解析
16. 如图所示是一个长方形．

(1)、根据图中尺寸大小，用含 $x$ 的代数式表示阴影部分的面积 $S$ ；

(2)、若 $x = 3$ ，求 $S$ 的值．

查看试题解析
17. 有理数a、b、c在数轴上的位置如图：

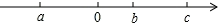(1)、判断正负，用“＞”或“＜”填空：b﹣c 0，b﹣a 0，c﹣a 0．

(2)、化简：|b﹣c|+|b﹣a|﹣|c﹣a|．

查看试题解析
18. 已知代数式 A=3x²﹣x+1，马小虎同学在做整式加减运算时，误将“A﹣B” 看成“A+B”了，计算的结果是 2 x²﹣3x﹣2．

(1)、请你帮马小虎同学求出正确的结果；

(2)、x 是最大的负整数，将 x 代入（1）问的结果求值．

查看试题解析

19. 某自行车广一周计划生产1050辆自行车，平均每天生产150辆，由于各种原因实际每天生产量与计划量相比有出入，下表是某周的生产情况（超产为正、减产为负）：

星期	一	二	三	四	五	六	日
增减	+5	-2	-4	+13	-10	+16	-9

(1)、根据记录可知前三天共生产多少辆？

(2)、产量最多的一天比生产量最少的一天多生产多少辆？

(3)、该厂实行计划工资制，每辆车50元，超额完成任务每辆奖10元，少生产一辆扣10元，那么该厂工人这一周的工资总额是多少？

查看试题解析

20. 若 A = 2x² + xy + 3y² ， B = x² - xy + 2 y² ．

(1)、若（1+ x）²与 $| 2 x - y + 2 |$ 为相反数，求2A-3（2B-A）的值；

(2)、若 x² + y²= 4， xy = -2 ，求 $A - B$ 的值．

查看试题解析
21. 观察下列各式：
$1^{2} = \frac{1 \times 2 \times 3}{6}$ ； $1^{2} + 2^{2} = \frac{2 \times 3 \times 5}{6}$ ； $1^{2} + 2^{2} + 3^{2} = \frac{3 \times 4 \times 7}{6}$ ； $1^{2} + 2^{2} + 3^{2} + 4^{2} = \frac{4 \times 5 \times 9}{6}$ ；……

(1)、根据你发现的规律，计算下面算式的值： $1^{2} + 2^{2} + 3^{2} + 4^{2} + 5^{2} =$ ；

(2)、请用一个含n的算式表示这个规律： $1^{2} + 2^{2} + 3^{2} + \dots + n^{2} =$ ；

(3)、根据发现的规律，请计算算式 $51^{2} + 52^{2} + \dots + 99^{2} + 100^{2}$ 的值（写出必要的解题过程）.

查看试题解析
22. 盐外第18届运动会，初一某班需要购买运动鞋和短裤，运动鞋每双定价200元，短裤每条定价50元．某商店开展促销活动，可以同时向客户提供两种优惠方案：
方案一：买一双运动鞋送一条短裤；

方案二：运动鞋和短裤都按定价的90%付款．

现某班要购买运动鞋20双，短裤x条（x超过20）．

(1)、若该班按方案一购买，需付款元；若该班按方案二购买，需付款元（用含x式子表示）；

(2)、当x=30时，哪种方案更划算？请通过计算说明理由；

(3)、若两种方案可以同时使用，当x=40时，你能给出一种最为省钱的购买方案吗？试写出你的购买方案，并计算该方案所需要付款金额．

查看试题解析
23. “幸福是奋斗出来的”，在数轴上，若C到A的距离刚好是3，则C点叫做A的“幸福点”，若C到A、B的距离之和为6，则C叫做A、B的“幸福中心”

(1)、如图1，点A表示的数为﹣1，则A的幸福点C所表示的数应该是；

(2)、如图2，M、N为数轴上两点，点M所表示的数为4，点N所表示的数为﹣2，点C就是M、N的幸福中心，则C所表示的数可以是（填一个即可）；

(3)、如图3，A、B、P为数轴上三点，点A所表示的数为﹣1，点B所表示的数为4，点P所表示的数为8，现有一只电子蚂蚁从点P出发，以2个单位每秒的速度向左运动，当经过多少秒时，电子蚂蚁是A和B的幸福中心？

查看试题解析