江西省吉安市2021-2022学年七年级上学期期中数学试题
试卷更新日期:2021-12-08 类型:期中考试
一、单选题
-
1. 单项式 的系数与次数分别是( )A、 B、 C、 D、2. 自新冠疫情爆发以来,全球经济遭受巨大损失,人民生命安全受到巨大威胁.2020年10月29日,据世卫组织最新统计数据显示:全球新冠肺炎确诊病例超4376万例,其中43760000用科学记数法表示为( )A、 B、 C、 D、3. 若一个棱柱有7个面,则它是( )A、七棱柱 B、六棱柱 C、五棱柱 D、四棱柱4. 如果a+b>0,且ab<0,那么( )A、a>0,b>0 B、a<0,b<0 C、a、b异号 D、a、b异号且正数的绝对值较大5. A站与B站之间还有3个车站,那么往返于A站与B站之间的车辆,应安排多少种车票?( )A、4 B、20 C、10 D、96. 图1是长为 ,宽为 的小长方形纸片将6张如图1的纸片按图2的方式不重叠地放在长方形 内,已知 的长度固定不变, 的长度可以变化,图中阴影部分(即两个长方形)的面积分别表示为 , ,若 ,且 为定值,则 , 满足的关系是( )
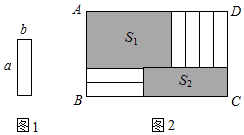 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 圆柱的侧面展开图是形.8. 计算 的值是 .9. 当k= 时,多项式 +(k-1)xy-3 -5中不含xy项.10. 如图,数轴上的点A所表示的数为a,化简|a|﹣|a﹣4|的结果为 .
 11. 如图,C,D是线段AB上两点,CB=3cm,DB=5cm,D是AC的中点,则线段AB的长为cm.
11. 如图,C,D是线段AB上两点,CB=3cm,DB=5cm,D是AC的中点,则线段AB的长为cm. 12. 在平面上有三点,过其中任意两点画直线,可画直线的条数为条.
12. 在平面上有三点,过其中任意两点画直线,可画直线的条数为条.三、解答题
-
13. 计算:(1)、 ;(2)、 ;14. 已知下列各有理数:﹣2.5,0,﹣|﹣3|,﹣(﹣2), ,﹣1.(1)、画出数轴,在数轴上标出这些数表示的点;(2)、用“<”号把这些数连接起来.15. 如图,是由大小相同的小立方块搭成的几何体,请在方格里画出从左面、上面观察这个图形所看到的形状图.
 16. 计算: .17. 如图,已知点C在线段AB上,点M,N分别在线段AC与线段BC上,且AM=2MC,BN=2NC.若AC=9,BC=6,求线段MN的长.
16. 计算: .17. 如图,已知点C在线段AB上,点M,N分别在线段AC与线段BC上,且AM=2MC,BN=2NC.若AC=9,BC=6,求线段MN的长. 18. 一名足球守门员练习折返跑,从球门的位置出发,向前记作正数,返回记作负数,他的记录如下(单位:米): .(1)、守门员是否回到了原来的位置?(2)、守门员离开球门的位置最远是多少?(3)、守门员一共走了多少路程?19. 已知代数式 , .(1)、当 , 时,求 的值;(2)、若 的值与 的取值无关,求 的值.20. 有一种牛奶软包装盒如图1所示.为了生产这种包装盒,需要先画出展开图纸样.
18. 一名足球守门员练习折返跑,从球门的位置出发,向前记作正数,返回记作负数,他的记录如下(单位:米): .(1)、守门员是否回到了原来的位置?(2)、守门员离开球门的位置最远是多少?(3)、守门员一共走了多少路程?19. 已知代数式 , .(1)、当 , 时,求 的值;(2)、若 的值与 的取值无关,求 的值.20. 有一种牛奶软包装盒如图1所示.为了生产这种包装盒,需要先画出展开图纸样. (1)、如图2给出三种纸样甲、乙、丙,在甲、乙、丙中,正确的有 .(2)、利用你所选的一种纸样,求出包装盒的侧面积和表面积(侧面积与两个底面积的和)21. 已知在纸面上有一数轴(如图),折叠纸面.例如:若数轴上数2表示的点与数 表示的点重合,则数轴上数 表示的点与数4表示的点重合.
(1)、如图2给出三种纸样甲、乙、丙,在甲、乙、丙中,正确的有 .(2)、利用你所选的一种纸样,求出包装盒的侧面积和表面积(侧面积与两个底面积的和)21. 已知在纸面上有一数轴(如图),折叠纸面.例如:若数轴上数2表示的点与数 表示的点重合,则数轴上数 表示的点与数4表示的点重合.
根据你对例题的理解,解答下列问题:
若数轴上数 表示的点与数1表示的点重合.(根据此情境解决下列问题)
(1)、则数轴上数3表示的点与数表示的点重合;(2)、若点 到原点的距离是5个单位长度,并且 、 两点经折叠后重合,则 点表示的数是;(3)、若数轴上 、 两点之间的距离为2020(点M在点N的右侧),并且 、 两点经折叠后重合,则 点表示的数是 , 则 点表示的数是 .22. 小雨同学在用黑色的围棋进行摆放图案的游戏,现已摆放了如下的图案,请根据图中的信息完成下列的问题. (1)、填写下表:
(1)、填写下表:图形编号
①
②
③
…
…
图中棋子的总数
…
…
(2)、第50个图形中棋子为颗围棋;(3)、小雨同学如果继续摆放下去,那么第 个图案就要用颗围棋.(4)、如果小雨同学手上刚好有90颗围棋子,那么他按照这种规律从①个图案摆放下去,是否可以摆放成完整的图案后刚好90颗围棋子一颗不剩?如果可以,那么刚好摆放完成几个完整的图案?如果不行,那么最多可以摆放多少个完整图案,还剩余几颗围棋子?(只答结果,不说明理由)23. 如图,点C在线段AB上,点M、N分别是线段AC、BC的中点. (1)、若 ,求线段 的长度;(2)、若 ,其他条件不变,请猜想线段 的长度,并说明理由;(3)、若点C在线段AB的延长线上, , ,其它条件不变,则线段MN的长度会有变化吗?若有变化,请直接写出结果,不说明理由.
(1)、若 ,求线段 的长度;(2)、若 ,其他条件不变,请猜想线段 的长度,并说明理由;(3)、若点C在线段AB的延长线上, , ,其它条件不变,则线段MN的长度会有变化吗?若有变化,请直接写出结果,不说明理由.