山东省泰安市新泰市2021-2022学年七年级上学期期中数学试题
试卷更新日期:2021-12-08 类型:期中考试
一、单选题
-
1. 下列长度的三条线段,能组成三角形的是( )A、1,3,4 B、5,6,12 C、5,7,2 D、6,8,102. 下列四个图中,正确画出△ABC中BC边上的高是( )A、
 B、
B、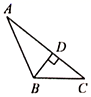 C、
C、 D、
D、 3. 下列图形中,是轴对称图形的是( ).A、
3. 下列图形中,是轴对称图形的是( ).A、 B、
B、 C、
C、 D、
D、 4. 如图, 、 、 、 四点在同一直线上,在 和 中, , ,添加下列条件,仍不能证明 的是( )
4. 如图, 、 、 、 四点在同一直线上,在 和 中, , ,添加下列条件,仍不能证明 的是( )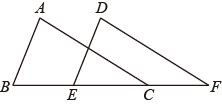 A、 B、 C、 D、5. 如图所示,已知 是 的角平分线, 于点 , , , ,则 的长为( ).
A、 B、 C、 D、5. 如图所示,已知 是 的角平分线, 于点 , , , ,则 的长为( ). A、3 B、6 C、9 D、126. 在 中, 、 、 的对边分别为 、 、 ,下列条件中,能判断 是直角三角形的有( )个.
A、3 B、6 C、9 D、126. 在 中, 、 、 的对边分别为 、 、 ,下列条件中,能判断 是直角三角形的有( )个.① , , ; ② ;③ ;④ , , .
A、1 B、2 C、3 D、47. 如图,已知 ,按下面步骤作图:
(1)在射线 上任意取一点 ,以点 为圆心, 长为半径作弧 ,交射线 于点 ,连接 ;(2)分别以点 , 为圆心, 长为半径作弧,两弧在 内部交于点 ,连接 , ;(3)作射线 交 于点 .根据以上所作图形,有如下结论,其中错误的是( ).
A、 B、 C、 D、8. 如图,在 中, 是 的垂直平分线, , 的周长为 ,则 的周长是( ). A、 B、 C、 D、9. 已知等腰三角形一腰上的高线与另一腰的夹角为 ,那么这个等腰三角形的顶角等于( ).A、 或 B、 C、 D、 或10. 如图,已知 ≌ , 是 的平分线,已知 , ,则 的度数是( ).
A、 B、 C、 D、9. 已知等腰三角形一腰上的高线与另一腰的夹角为 ,那么这个等腰三角形的顶角等于( ).A、 或 B、 C、 D、 或10. 如图,已知 ≌ , 是 的平分线,已知 , ,则 的度数是( ).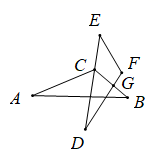 A、 B、 C、 D、11. 如图,在 的正方形网格中,有5个小正方形已被涂黑(图中阴影部分),若在其余网格中再涂黑一个小正方形,使它与5个已被涂黑的小正方形组成的新图形是一个轴对称图形,则可涂黑的小正方形共有( )个.
A、 B、 C、 D、11. 如图,在 的正方形网格中,有5个小正方形已被涂黑(图中阴影部分),若在其余网格中再涂黑一个小正方形,使它与5个已被涂黑的小正方形组成的新图形是一个轴对称图形,则可涂黑的小正方形共有( )个.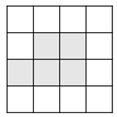 A、2 B、3 C、4 D、512. 如图,牧童在 处放牛,牧童家在 处, , 处距河岸 的距离 、 的长分别为5km和10km,且 , 两点的距离为8km,天黑前牧童从 处将牛牵到河边饮水再回家,那么牧童最少要走的距离为( ).
A、2 B、3 C、4 D、512. 如图,牧童在 处放牛,牧童家在 处, , 处距河岸 的距离 、 的长分别为5km和10km,且 , 两点的距离为8km,天黑前牧童从 处将牛牵到河边饮水再回家,那么牧童最少要走的距离为( ). A、15km B、16km C、17km D、18km
A、15km B、16km C、17km D、18km二、填空题
-
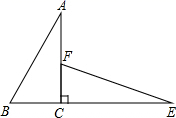
13. 如图, , , , , ,则 .
 14. 如图,在 中, , , .若 的垂直平分线交 于点 ,交 于点 , 的垂直平分线交 于点 ,交 于点 ,则 .
14. 如图,在 中, , , .若 的垂直平分线交 于点 ,交 于点 , 的垂直平分线交 于点 ,交 于点 ,则 . 15. 对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形 ,对角线 、 交于点 .若 , ,则 .
15. 对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形 ,对角线 、 交于点 .若 , ,则 . 16. 《九章算术》是我国古代数学的经典著作,书中有一个“折竹抵地”问题:“今有竹高丈,末折抵地,问折者高几何?”意思是:一根竹子,原来高一丈(一丈为十尺),虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子根部三尺远,那么原处还有尺高的竹子.
16. 《九章算术》是我国古代数学的经典著作,书中有一个“折竹抵地”问题:“今有竹高丈,末折抵地,问折者高几何?”意思是:一根竹子,原来高一丈(一丈为十尺),虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子根部三尺远,那么原处还有尺高的竹子. 17. 如图所示,校园有一块四边形草坪 ,测得 , m, m, m, m,则这块四边形草坪的面积是m2 .
17. 如图所示,校园有一块四边形草坪 ,测得 , m, m, m, m,则这块四边形草坪的面积是m2 . 18. 如图,在 中, ,点D是 的中点,点E在 上,将 沿 折叠,若点B的落点 在射线 上,则 与 所夹锐角的度数是 .
18. 如图,在 中, ,点D是 的中点,点E在 上,将 沿 折叠,若点B的落点 在射线 上,则 与 所夹锐角的度数是 .
三、解答题
-
19. 如图,方格纸中每个小方格都是边长为1个单位的正方形,已知 的三个顶点在格点上.
 (1)、画出 ,使它与 关于直线a对称;(2)、求出 的面积;(3)、在直线a上画出点P,使 最小20. 如图,在 中, 是 边上的高线, 的垂直平分线分别交 , 于点 , .
(1)、画出 ,使它与 关于直线a对称;(2)、求出 的面积;(3)、在直线a上画出点P,使 最小20. 如图,在 中, 是 边上的高线, 的垂直平分线分别交 , 于点 , . (1)、若 ,求 的度数;(2)、若 ,求 的度数.21. 如图所示,在四边形 中, , 为 的中点,连接 、 , ,延长 交 的延长线于点 .求证:
(1)、若 ,求 的度数;(2)、若 ,求 的度数.21. 如图所示,在四边形 中, , 为 的中点,连接 、 , ,延长 交 的延长线于点 .求证: (1)、 ;(2)、 平分 .22. 如图,在 中, , 于点 , 的平分线 交 于点 .
(1)、 ;(2)、 平分 .22. 如图,在 中, , 于点 , 的平分线 交 于点 . (1)、求证: ;(2)、若 , ,求 的长.23. 如图,△ABC中,BC=2AC,∠DBC=∠ACB=120°,BD=BC,CD交边AB于点E.
(1)、求证: ;(2)、若 , ,求 的长.23. 如图,△ABC中,BC=2AC,∠DBC=∠ACB=120°,BD=BC,CD交边AB于点E.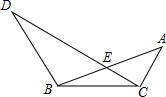 (1)、求∠ACE的度数.(2)、求证:DE=3CE.
(1)、求∠ACE的度数.(2)、求证:DE=3CE.

