黑龙江省大庆市龙凤区2021-2022学年七年级上学期期中数学试题
试卷更新日期:2021-12-08 类型:期中考试
一、单选题
-
1. 清代·袁枚的一首诗《苔》中的诗句:“白日不到处,青春恰自来.苔花如米小,也学牡丹开.”若苔花的花粉直径约为0.0000084米,则数据0.0000084用科学记数法表示为( )A、8.4×10-5 B、8.4×10-6 C、84×10-7 D、8.4×1062. 下列运算正确的是( )A、a+2a=3a2 B、 C、 D、3. 下列命题中,是真命题的是( )A、同位角相等 B、同角的余角相等 C、相等的角是对顶角 D、有且只有一条直线与已知直线垂直4. 如图,AD是Rt△ABC的斜边BC上的高,则图中与∠B互余的角有( )
 A、1个 B、2个 C、3个 D、4个5. 如图,直线 被直线 所截下列条件能判定 的是( )
A、1个 B、2个 C、3个 D、4个5. 如图,直线 被直线 所截下列条件能判定 的是( ) A、 B、 C、 D、6. 如图,用尺规作图作∠AOC=∠AOB的第一步是以点O为圆心,以任意长为半径画弧①,分别交OA,OB于点E,F,那么第二步的作图痕迹②的作法是( )
A、 B、 C、 D、6. 如图,用尺规作图作∠AOC=∠AOB的第一步是以点O为圆心,以任意长为半径画弧①,分别交OA,OB于点E,F,那么第二步的作图痕迹②的作法是( )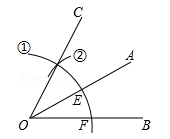 A、以点F为圆心,OE长为半径画弧 B、以点F为圆心,EF长为半径画弧 C、以点E为圆心,OE长为半径画弧 D、以点E为圆心,EF长为半径画弧7. 某学生上学路线如图所示,他总共拐了三次弯,最后行车路线与开始的路线相互平行,已知第一次转过的角度,第三次转过的角度,则第二次拐弯角 的度数是( )
A、以点F为圆心,OE长为半径画弧 B、以点F为圆心,EF长为半径画弧 C、以点E为圆心,OE长为半径画弧 D、以点E为圆心,EF长为半径画弧7. 某学生上学路线如图所示,他总共拐了三次弯,最后行车路线与开始的路线相互平行,已知第一次转过的角度,第三次转过的角度,则第二次拐弯角 的度数是( ) A、 B、 C、 D、8. 记 ,且 ,则 ( ).A、128 B、32 C、64 D、169. 如图,将四边形纸片ABCD沿PR翻折得到三角形PC′R,恰好C′P∥AB,C′R∥AD.若∠B=120°,∠D=50°,则∠C=( )
A、 B、 C、 D、8. 记 ,且 ,则 ( ).A、128 B、32 C、64 D、169. 如图,将四边形纸片ABCD沿PR翻折得到三角形PC′R,恰好C′P∥AB,C′R∥AD.若∠B=120°,∠D=50°,则∠C=( ) A、85° B、95° C、90° D、80°10. 下列有四个结论,其中正确的是( )
A、85° B、95° C、90° D、80°10. 下列有四个结论,其中正确的是( )①若 ,则 只能是 ;②若 的运算结果中不含 项,则 ③若 , ,则 ④若 , ,则 可表示为
A、①②③④ B、②③④ C、①③④ D、②④二、填空题
-
11. 已知 ,则 的补角 .12. 如图,直线 、 相交于点 , ,垂足为点 , ,则 .
 13. 如果 是一个完全平方式,那么m的值为.14. 若 , ,则 .15. 已知 ,则 .16. 请看杨辉三角 ,并观察等式
13. 如果 是一个完全平方式,那么m的值为.14. 若 , ,则 .15. 已知 ,则 .16. 请看杨辉三角 ,并观察等式
根据前面各式的规律,则你猜想 的展开式中含 项的系数是 .
17. 如图所示,在三角形 中,已知 ,高 ,动点 由点 沿 向点 移动 不与点 重合 设 的长为 ,三角形 的面积为 ,则 与 之间的关系式为 .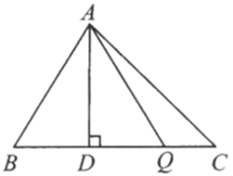 18. 已知 , 若用只含有 的代数式表示 ,则 .19. 已知 ,则代数式 的值是 .20. 甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示,当乙到达终点A时,甲还需分钟到达终点B.
18. 已知 , 若用只含有 的代数式表示 ,则 .19. 已知 ,则代数式 的值是 .20. 甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示,当乙到达终点A时,甲还需分钟到达终点B.
三、解答题
-
21.(1)、 ;(2)、 ;(3)、 ;(4)、先化简,再求值: ,其中 .(5)、已知 ,求代数式 的值.22. 如图,已知EF∥AD, 试说明 请将下面的说明过程填写完整.

解: EF∥AD, 已知
▲ ▲
又 , 已知
, ▲
∥ ▲ , ▲
▲
23. 长方形的一边长是 ,其邻边长为 ,周长是 ,面积为 .(1)、写出 和 之间的关系式(2)、写出 和 之间的关系式(3)、当 时, 等于多少 等于多少(4)、当 增加 时, 增加多少 增加多少24. 已知一个角的两边与另一个角的两边分别平行,分别结合下图,试探索这两个角的关系,并证明你的结论.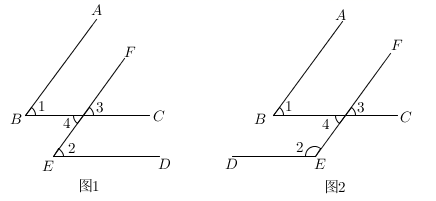 (1)、如图1,AB∥EF,BC∥DE, 与 的关系是 .(2)、如图2,AB∥EF,BC∥DE, 与 的关系是 .(3)、经过上述证明,我们可以得到一个结论:(4)、若两个角的两边分别平行,且一个角比另一个角的 倍少 ,则这两个角分别是多少度?25. 将长为 、宽为 的长方形白纸,按如图所示的方法黏合起来,黏合部分宽为 .
(1)、如图1,AB∥EF,BC∥DE, 与 的关系是 .(2)、如图2,AB∥EF,BC∥DE, 与 的关系是 .(3)、经过上述证明,我们可以得到一个结论:(4)、若两个角的两边分别平行,且一个角比另一个角的 倍少 ,则这两个角分别是多少度?25. 将长为 、宽为 的长方形白纸,按如图所示的方法黏合起来,黏合部分宽为 . (1)、根据图,将表格补充完整:
(1)、根据图,将表格补充完整:白纸张数
1
2
3
4
5
纸条长度
40
110
145
(2)、设 张白纸黏合后的总长度为 ,则 与 之间的关系式是什么?(3)、你认为白纸黏合起来总长度可能为 吗?为什么?26. 已知:如图,EF∥CD,∠1+∠2=180° (1)、判断GD与CA的位置关系,并说明理由;(2)、若CD平分∠ACB,DG平分∠CDB,且∠A=40°,求∠ACB的度数。27. 已知动点P以2cm/s的速度沿图1所示的边框从B-C-D-E-F-A的路径运动,记△ABP的面积为S(cm2),S与运动时间t(s)的关系如图2所示,若AB=6cm,请回答下列问题:
(1)、判断GD与CA的位置关系,并说明理由;(2)、若CD平分∠ACB,DG平分∠CDB,且∠A=40°,求∠ACB的度数。27. 已知动点P以2cm/s的速度沿图1所示的边框从B-C-D-E-F-A的路径运动,记△ABP的面积为S(cm2),S与运动时间t(s)的关系如图2所示,若AB=6cm,请回答下列问题: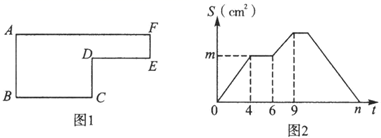 (1)、图1中BC= cm,CD= cm,DE= cm;(2)、求图2中m、n的值.28. 如图 ,MN∥PQ,直线 与 、 分别交于点 、 ,点 在直线 上,过点 作 ,垂足为点 .
(1)、图1中BC= cm,CD= cm,DE= cm;(2)、求图2中m、n的值.28. 如图 ,MN∥PQ,直线 与 、 分别交于点 、 ,点 在直线 上,过点 作 ,垂足为点 .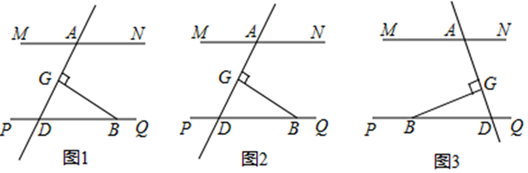 (1)、求证: ;(2)、若点 在线段 上 不与 、 、 重合 ,连接 , 和 的平分线交于点 ,请在图 中补全图形,猜想并证明 与 的数量关系;(3)、若直线 的位置如图 所示,(2)中的结论是否成立?若成立,请证明;若不成立,请直接写出 与 的数量关系.
(1)、求证: ;(2)、若点 在线段 上 不与 、 、 重合 ,连接 , 和 的平分线交于点 ,请在图 中补全图形,猜想并证明 与 的数量关系;(3)、若直线 的位置如图 所示,(2)中的结论是否成立?若成立,请证明;若不成立,请直接写出 与 的数量关系.