广东省中山市2021-2022学年七年级上学期期中数学试题

试卷更新日期：2021-12-08 类型：期中考试

进入出卷网下载

一、单选题

1. -2021的倒数是（）

A、-2021 B、 $\frac{1}{2021}$ C、2021 D、 $- \frac{1}{2021}$

查看试题解析
2. 在下列数： $- \frac{5}{6}$ ，＋1，6.7，－15，－1中，属于分数的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
3. 经历百年风雨，中国共产党从小到大、由弱到强，从建党时50多名党员发展成为今天已经拥有超过9500万党员的世界第一大政党.9500万用科学记数法表示为（）

A、9.5×10⁸ B、9.5×10⁷ C、9.5×10⁶ D、9.5×10³

查看试题解析
4. 在下列整式中，次数为3的单项式是（）

A、 $a^{3} - b^{3}$ B、 $x y^{2}$ C、 $s^{3} t$ D、 $3 m n$

查看试题解析
5. 下列运算正确的是（）

A、 $- 2^{2} = 4$ B、 $- | - 1 | = - 1$ C、 $2 x - x = 2$ D、 $2 x^{2} + 3 x^{3} = 5 x^{5}$

查看试题解析
6. 下列说法中，正确的是（）

A、单项式 $\frac{1}{2} x y^{2}$ 的系数 $\frac{1}{2} x$ B、单项式 $- 5 x^{2}$ 的次数为-5 C、多项式 $x^{2} + 2 x + 18$ 是二次三项式 D、多项式 $x^{2} + y^{2} - 1$ 的常数项是1

查看试题解析
7. 不改变式子a－（2b－4c）的值，去掉括号后结果正确的是（）

A、a－2b＋4c B、a＋2b＋4c C、a－2b－4c D、a＋2b－4c

查看试题解析
8. 如图，数轴上A、B两点之间的距离是3，点B在点A左侧，那么点B表示的数是（）

A、3 B、﹣3 C、1 D、﹣1

查看试题解析
9. 若|x|＝5，y³＝8且x＜0，则x＋y＝（）

A、7 B、－3 C、7或－7 D、3或－3

查看试题解析
10. 正六边形ABCDEF在数轴上的位置如图，点A、F对应的数分别为0和1，若正六边形ABCDEF绕着顶点顺时针方向在数轴上连续翻转，翻转1次后，点E所对应的数为2，则连续翻转2021次后，数轴上2021这个数所对应的点是（）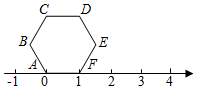

A、A点 B、B点 C、C点 D、D点

查看试题解析

二、填空题

11. 如果收入100元记作＋100元，则支出20元记作元．

查看试题解析
12. 近似数7.80千克精确到．

查看试题解析
13. “比x的2倍小－3的数”用式子表示是．

查看试题解析
14. 若7a^xb²与－3a³b^y的和为单项式，则x^y＝．

查看试题解析
15. 已知a+b＝3，c﹣b＝12，则a+2b﹣c的值为．

查看试题解析
16. 如图是一个数值运算的程序，若输出y的值为1，则输入的值为．

查看试题解析
17. 观察下列图中所示的一系列图形，它们是按一定规律排列的，依照此规律，第10个图形共有个○．

查看试题解析

三、解答题

18. 计算：－（－3）＋7－2－|－8|．

查看试题解析
19. 合并同类项： $5 a^{2} - 7 - 3 a - 5 + 3 a - 2 a^{2}$ .

查看试题解析
20. 在数轴上表示下列各数，并按照从小到大的顺序用“ ＜ ”连接起来．
＋3，－1， $- (- 4 \frac{1}{2})$ ，0，－2 $\frac{1}{2}$ ，－2² ， |－0.5|

查看试题解析
21. 计算：－12×（－9）＋16÷（－2）³－|－4×5|

查看试题解析
22. 小明参加“趣味数学”选修课，课上老师给了一个问题，小明看了很为难，你能帮他一下吗？若a，b互为相反数，c，d互为倒数，|m|=2，求a－（－b）－ $\frac{m}{c d}$ 的值．

查看试题解析
23. 定义：若 $m + n = 2$ ，则称 $m$ 与 $n$ 是关于1的平衡数．

(1)、3与是关于1的平衡数， $5 - x$ 与（用含 $x$ 的整式表示）是关于1的平衡数；

(2)、若 $a = 2 x^{2} - 3 (x^{2} + x) + 4$ ， $b = 2 x - [3 x - (4 x + x^{2}) - 2]$ ，判断 $a$ 与 $b$ 是否是关于1的平衡数，并说明理由．

查看试题解析

24. 某校七年级1至4班计划每班购买数量相同的图书布置班级读书角，但是由于种种原因，实际购书量与计划有出入，如表是实际购书情况：

班级	1班	2班	3班	4班
实际购买数量	a	33	c	21
实际购买量与计划购买量的差值	12	b	-8	-9

(1)、直接写出a= ，b＝，c＝；

(2)、根据记录的数据可知4个班计划每班购书本；

(3)、书店给出一种优惠方案：一次购买不少于15本，其中2本书免费．若每本书售价为25元，请计算这4个班整体购书的最低总花费是多少元？

查看试题解析

25. 如图，点A，B，C是数轴上三点，点C表示的数为6，BC＝4，AB＝12

(1)、写出数轴上点A，B表示的数：，；

(2)、动点P，Q同时从A，C出发，点P以每秒4个单位长度的速度沿数轴向右匀速运动，点Q以每秒2个单位长度的速度沿数轴向左匀速运动，设运动时间为t （t＞0）秒．
①当t＝2时，求出此时P，Q在数轴上表示的数；

②t为何值时，点P，Q相距2个单位长度，并写出此时点P，Q在数轴上表示的数．

查看试题解析