山西省运城市盐湖区2021-2022学年九年级上学期期中数学试题

试卷更新日期：2021-12-08 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程中属于一元二次方程的是（）

A、 $x (x + 5) = x^{2} - 2$ B、 $\frac{1}{x^{2}} + \frac{1}{x} = 0$ C、 $a x^{2} + b x + c = 0$ D、 $2 {(y + 1)}^{2} = y + 1$

查看试题解析
2. 有一个只放满形状大小都一样的白色小球的不透明盒子，小刚想知道盒内有多少白球，于是小刚向这个盒中放了5个黑球（黑球的形状大小与白球一样），摇匀后从中随机摸出一个球记下颜色，再把它放回盒中，不断重复，共摸球400次，其中80次摸到黑球，则盒中白色小球的个数可能是（）

A、16个 B、20个 C、24个 D、25个

查看试题解析
3. 将一元二次方程 $x^{2} + 4 x - 1 = 0$ 化成 ${(x - a)}^{2} = b$ （a，b为常数）的形式，a，b的值分别为（）

A、 $a = 2 ， b = 3$ B、 $a = 2 ， b = 5$ C、 $a = - 2 ， b = 3$ D、 $a = - 2 ， b = 5$

查看试题解析
4. 如图，小颖把一面镜子水平放置在离树底（点B）8米的点E处，然后沿着直线BE后退到点D，这时恰好在镜子里看到树梢（点A），已知 $D E = 4$ 米，小颖目高 $C D = 1.6$ 米，则树的高度AB为（）

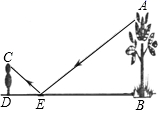A、3.2米 B、4.8米 C、8米 D、20米

查看试题解析
5. 若关于x的一元二次方程 $(m - 3) x^{2} + 3 x + 1 = 0$ 有实数根，则m的取值范围中，正整数值有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
6. 如图，在△ABC中，点E、D、F分别在边AB、BC、CA上，且DE∥CA，DF∥BA．下列四个判断中，错误的是（）

A、四边形AEDF是平行四边形 B、如果∠BAC＝90°，那么四边形AEDF是矩形 C、如果AD平分∠BAC，那么四边形AEDF是菱形 D、如果AD⊥BC且BD＝CD，那么四边形AEDF是正方形

查看试题解析
7. 某超市今年二月份的营业额为82万元，四月份的营业额比三月份的营业额多20万元，若二月份到四月份每个月的月销售额增长率都相同，若设增长率为x，根据题意可列方程（）

A、82（1+x）²＝82（1+x）+20 B、82（1+x）²＝82（1+x） C、82（1+x）²＝82+20 D、82（1+x）＝82+20

查看试题解析
8. 如图，在菱形ABCD中，点E、F、G、H分别是边AB、BC、CD和DA的中点，连接EF、FG、GH和HE．若EH＝2EF，则下列结论正确的是（）

A、AB＝ $\sqrt{2}$ EF B、AB＝2EF C、AB＝ $\sqrt{3}$ EF D、AB＝ $\sqrt{5}$ EF

查看试题解析
9. 如果两个相似三角形的对应边之比为2：5，其中一个三角形的一个内角的角平分线长为7，则另一个三角形对应角平分线的长为（）

A、 $\frac{35}{2}$ B、 $\frac{14}{5}$ C、 $\frac{35}{2}$ 或 $\frac{14}{5}$ D、无法确定

查看试题解析
10. 如图，在正方形ABCD中，E为AD上的点，连接CE．①以点E为圆心，以任意长为半径作弧分别交EC，ED于点N，M；②分别以M，N为圆心，以大于 $\frac{1}{2} M N$ 长为半径作弧，两弧在 $∠ C E D$ 内交于点P；③连接EP并延长交DC于点H，交BC的延长线于点G．若 $A B = 16$ ， $A E ： A D = 1 ： 4$ ，则EH的长为（）

A、14 B、 $6 \sqrt{5}$ C、16 D、 $8 \sqrt{3}$

查看试题解析

二、填空题

11. 已知 $\frac{a}{b} = \frac{c}{d} = \frac{e}{f} = \frac{4}{3}$ ．若 $b + d + f = 6$ ．则 $a + c + e$ 的值为．

查看试题解析
12. 某品牌汽车为了打造更加精美的外观，特将汽车倒车镜设计为整个车身黄金分割点的位置（如图），若车头与倒车镜的水平距离为1.58m，则该车车身总长约为m．（结果精确到0.01m）

查看试题解析
13. 如图，在长为32米，宽为20米的矩形地面上：修建如图所示的道路（图中的阴影部分），余下部分铺设草坪，要使得草坪的面积为540平方米，则可列方程为．

查看试题解析
14. 如图，四边形ABCD和 $A^{'} B^{'} C^{'} D^{'}$ 是以点O为位似中心的位似图形，若 $O A ： O A^{'} = 3 ： 5$ ，则四边形ABCD与四边形 $A^{'} B^{'} C^{'} D^{'}$ 的面积比是．

查看试题解析
15. 如图，在平面直角坐标系中，矩形ABCD的顶点C在x轴正半轴上，顶点A在y轴正半轴上，顶点B与坐标原点O重合， $A B = 2$ ， $B C = 3$ ，将矩形ABCD沿对角线AC裁开，将 $△ A D C$ 沿CA方向平移得到 $△ A^{'} D^{'} C^{'}$ ，连接 $A D^{'}$ ， $B C^{'}$ ，当四边形 $A B C^{'} D^{'}$ 为菱形时，点 $D^{'}$ 的坐标为．

查看试题解析

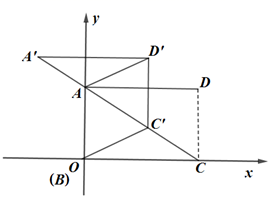
三、解答题

16. 解方程

(1)、 $x^{2} + 2 x - 1 = 0$

(2)、 $3 x (x - 1) = 2 - 2 x$

查看试题解析
17. 在 $R t △ A B C$ 中， $∠ A C B = 90 °$ 点D是边AB上的一个动点，连接CD．作 $A E ∥ D C$ ， $C E ∥ A B$ ，连接ED．

(1)、如图1，当 $C D ⊥ A B$ 时，求证： $A C = E D$ ；

(2)、如图2，当D是AB的中点时，
①四边形ADCE的形状是 ▲ ；请说明理由．

②若 $A B = 5$ ， $E D = 4$ ，则四边形ADCE的面积为 ▲ ．

查看试题解析
18. 北京将于2022年举办冬奥会和冬残奥会，中国将成为一个举办过五次各类奥林匹克运动会的国家小亮是个集邮爱好者，他收集了如下图所示的四张纪念邮票（除正面内容不同外，其余均相同），现将四张邮票背面朝上，洗匀放好．

(1)、小亮从中随机抽取一张邮票是“冬残奥会吉祥物雪容融”的概率是；

(2)、小亮从中随机抽取一张邮票（不放回），再从余下的邮票中随机抽取一张，请你用列表或画树状图的方法求抽到的两张邮票恰好是“冬奥会会徽”和“冬奥会吉祥物冰墩墩”的概率．（这四张邮票依次分别用字母A，B，C，D表示）

查看试题解析
19. 如图，正方形ABCD中，M为BC上点，F是AM的中点，过点F作 $E F ⊥ A M$ ，交AD的延长线于点E，交DC于点N．

(1)、求证： $△ A B M ∽ △ E F A$ ；

(2)、若 $A B = 6$ ， $B M = 2$ ，求DE的长．

查看试题解析
20. 某果商按每千克10元的价格收购了1000千克精品红富士苹果存入冷库中，预测这种苹果的市场价格平均每天每千克上涨0.5元，但冷库存放这批苹果时每天需要支出各种费用合计110元，同时，平均每天有3千克的苹果腐烂不能出售，而且这种苹果在冷库中最多能保存90天．

(1)、若该果商将这批苹果存放x天后一次性出售，则x天后这批苹果的销售单价为（）元，销售量为（）千克（用含x的代数式表示）；

(2)、这次销售后该果商共获得利润12000元，求这批苹果存放了多少天后出售？

查看试题解析
21. 阅读下列材料，完成任务
小明同学酷爱数学，勤于探索研究，他画了一个三角形ABC，并画出其中一个外角 $∠ C A E$ 的角平分线，与BC的延长线交于点N，小明通过测量发现，该图形中的线段有特殊的关系： $\frac{A B}{A C} = \frac{N B}{N C}$ ，他想证明自己的发现．下面是部分证明过程：

证明：过点C作 $C D ∥ A N$ 交AB于点D，则 $\frac{A B}{A D} = \frac{N B}{N C}$ （第一步），

∴ $∠ A C D = ∠ C A N$ ， $∠ A D C = ∠ E A N$ （第二步）

…

请回答下面问题：

(1)、小明部分证明过程中，第一步的依据是；

(2)、请完成证明的剩余部分；

(3)、若 $A B = 6 \sqrt{3}$ ， $A C = 6$ ， $∠ B A C = 30 °$ ，请求出CN的长．

查看试题解析
22. 如图1，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C$ ， $D$ 是 $A B$ 的中点．过点 $C$ 作射线 $C M$ 交 $A B$ 于点 $P$ （点 $P$ 不与点 $D$ 重合），过点 $B$ 作 $B E ⊥ C M$ 于点 $E$ ，连接 $D E$ ，过点 $D$ 作 $D F ⊥ D E$ 交 $C M$ 于点 $F$ ．

(1)、求证： $D E = D F$ ；

(2)、如图2，若 $A E = A C$ ，连接 $A F$ 并延长到点 $G$ ，使 $F G = A F$ ，连接 $C G$ ， $E G$ ，求证：四边形 $A C G E$ 为菱形；

(3)、在（2）的条件下，求 $\frac{A P}{B P}$ 的值．

查看试题解析
23. 综合与探究
如图，在平面直角坐标系中，点 $A (0 ， 10)$ ，点B是x轴的正半轴上的一个动点，连接AB，取AB的中点M，将线段MB绕着点B按顺时针方向旋转90°，得到线段BC．过点B作x轴的垂线交直线AC于点D．设点B坐标是 $(t ， 0)$

(1)、当 $t = 6$ 时，点M的坐标是；

(2)、用含t的代数式表示点C的坐标；

(3)、是否存在点B，使四边形AOBD为矩形？若存在，请求出点B的坐标；若不存在，请说明理由；

(4)、在点B的运动过程中，平面内是否存在一点N，使得以A、B、N、D为顶点的四边形是菱形？若存在，请直接写出点N的纵坐标（不必要写横坐标）；若不存在，请说明理由．

查看试题解析