山东省枣庄市峄城区2021-2022学年九年级上学期期中数学试题
试卷更新日期:2021-12-08 类型:期中考试
一、单选题
-
1. 如图所示的木制活动衣帽架是由三个全等的菱形构成,根据实际需要可以调节 间的距离,若 间的距离调节到60 ,菱形的边长 ,则 的度数是( )
 A、 B、 C、 D、2. 下列命题是真命题的是( )A、对角线互相垂直平分的四边形是正方形 B、对角线相等的四边形是平行四边形 C、对角线互相垂直的四边形是菱形 D、对角线互相平分且相等的四边形是矩形3. 如图,把含30°的直角三角板PMN放置在正方形ABCD中, ,直角顶点P在正方形ABCD的对角线BD上,点M,N分别在AB和CD边上,MN与BD交于点O,且点O为MN的中点,则 的度数为( )
A、 B、 C、 D、2. 下列命题是真命题的是( )A、对角线互相垂直平分的四边形是正方形 B、对角线相等的四边形是平行四边形 C、对角线互相垂直的四边形是菱形 D、对角线互相平分且相等的四边形是矩形3. 如图,把含30°的直角三角板PMN放置在正方形ABCD中, ,直角顶点P在正方形ABCD的对角线BD上,点M,N分别在AB和CD边上,MN与BD交于点O,且点O为MN的中点,则 的度数为( )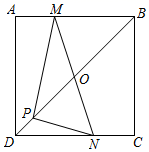 A、60° B、65° C、75° D、80°4. 用配方法解方程 时,配方结果正确的是( )A、 B、 C、 D、5. 对于一元二次方程 ,则它根的情况为( )A、没有实数根 B、两根之和是3 C、两根之积是-2 D、有两个不相等的实数根6. 已知方程 的两根分别为 , ,则 的值为( )A、1 B、-1 C、2021 D、-20217. 若直角三角形的两边长分别是方程 的两根,则该直角三角形的面积是( )A、6 B、12 C、12或 D、6或8. 如图, 分别是 边 上的点, ,若 ,则 的长是( ).
A、60° B、65° C、75° D、80°4. 用配方法解方程 时,配方结果正确的是( )A、 B、 C、 D、5. 对于一元二次方程 ,则它根的情况为( )A、没有实数根 B、两根之和是3 C、两根之积是-2 D、有两个不相等的实数根6. 已知方程 的两根分别为 , ,则 的值为( )A、1 B、-1 C、2021 D、-20217. 若直角三角形的两边长分别是方程 的两根,则该直角三角形的面积是( )A、6 B、12 C、12或 D、6或8. 如图, 分别是 边 上的点, ,若 ,则 的长是( ).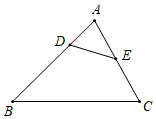 A、1 B、2 C、3 D、49. 下列说法中,正确的是( )A、若点M是 上一点,且满足 ,则M是 的黄金分割点 B、所有的菱形都相似 C、所有的矩形都相似 D、所有的等腰三角形都相似10. 图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面 ( )
A、1 B、2 C、3 D、49. 下列说法中,正确的是( )A、若点M是 上一点,且满足 ,则M是 的黄金分割点 B、所有的菱形都相似 C、所有的矩形都相似 D、所有的等腰三角形都相似10. 图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面 ( )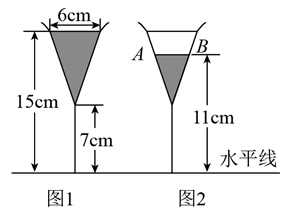 A、 B、 C、 D、11. 如图,在平面直角坐标系中,将 以原点O为位似中心放大后得到 ,若 , ,则 与 的相似比是( )
A、 B、 C、 D、11. 如图,在平面直角坐标系中,将 以原点O为位似中心放大后得到 ,若 , ,则 与 的相似比是( )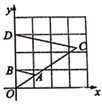 A、2:1 B、1:2 C、3:1 D、1:312. 现有4张卡片,正面图案如图所示,它们除此之外完全相同.把这4张卡片背面朝上洗匀,从中随机抽取两张,则这两张卡片正面图案恰好是“天问”和“九章”的概率是( )
A、2:1 B、1:2 C、3:1 D、1:312. 现有4张卡片,正面图案如图所示,它们除此之外完全相同.把这4张卡片背面朝上洗匀,从中随机抽取两张,则这两张卡片正面图案恰好是“天问”和“九章”的概率是( )


 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
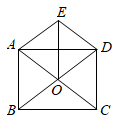
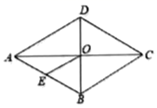
13. 如图,菱形 的对角线 相交于点O,点E是边 的中点,若 ,则菱形 的周长为 .
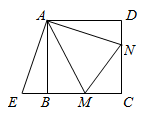
 14. 《九章算术》是我国古代数学名著,书中有下列问题:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”其意思为:今有一门,高比宽多6尺8寸,门对角线距离恰好为1丈.问门高、宽各是多少?(1丈=10尺,1尺=10寸)如图, 设门高 为 尺,根据题意,可列方程为 .
14. 《九章算术》是我国古代数学名著,书中有下列问题:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”其意思为:今有一门,高比宽多6尺8寸,门对角线距离恰好为1丈.问门高、宽各是多少?(1丈=10尺,1尺=10寸)如图, 设门高 为 尺,根据题意,可列方程为 . 15. 如图,在 中, ,过点B作 ,垂足为B,且 ,连接CD,与AB相交于点M,过点M作 ,垂足为N.若 ,则MN的长为 .
15. 如图,在 中, ,过点B作 ,垂足为B,且 ,连接CD,与AB相交于点M,过点M作 ,垂足为N.若 ,则MN的长为 .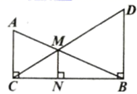 16. 如图,在实验桌上有完全相同的烧杯内装有体积相同且无色透明的3种液体,其中1杯酒精,3杯生理盐水,2杯白糖水,从中任取一杯为白糖水的概率是 .
16. 如图,在实验桌上有完全相同的烧杯内装有体积相同且无色透明的3种液体,其中1杯酒精,3杯生理盐水,2杯白糖水,从中任取一杯为白糖水的概率是 .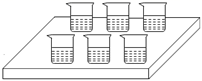 17. 如图,在 中, ,垂足为 , , ,四边形 和四边形 均为正方形,且点 、 、 、 、 、 都在 的边上,那么 与四边形 的面积比为 .
17. 如图,在 中, ,垂足为 , , ,四边形 和四边形 均为正方形,且点 、 、 、 、 、 都在 的边上,那么 与四边形 的面积比为 .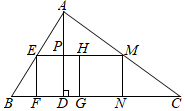 18. 如图,在边长为4的正方形ABCD中,点E是BC的中点,点F在CD上,且CF=3DF,AE,BF相交于点G,则△AGF的面积是.
18. 如图,在边长为4的正方形ABCD中,点E是BC的中点,点F在CD上,且CF=3DF,AE,BF相交于点G,则△AGF的面积是.
三、解答题
-
19. 小敏与小霞两位同学解方程 的过程如下框:
小敏:
两边同除以 ,得
,
则 .
小霞:
移项,得 ,
提取公因式,得 .
则 或 ,
解得 , .
你认为他们的解法是否正确?若正确请在框内打“√”;若错误请在框内打“×”,并写出你的解答过程.
20. 已知关于 的一元二次方程 有实数根.(1)、求 的取值范围;(2)、若该方程的两个实数根分别为 、 ,且 ,求 的值.21. 如图,在 中,D在 上, , . (1)、求证: ∽ ;(2)、若 ,求 的值.22. 某博物馆展厅的俯视示意图如图1所示,嘉淇进入展厅后开始自由参观,每走到一个十字道口,她自己可能直行,也可能向左转或向右转,且这三种可能性均相同.
(1)、求证: ∽ ;(2)、若 ,求 的值.22. 某博物馆展厅的俯视示意图如图1所示,嘉淇进入展厅后开始自由参观,每走到一个十字道口,她自己可能直行,也可能向左转或向右转,且这三种可能性均相同.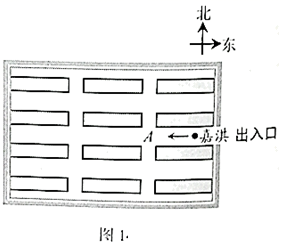
 (1)、求嘉淇走到十字道口 向北走的概率;(2)、补全图2的树状图,并分析嘉淇经过两个十字道口后向哪个方向参观的概率较大.23. 如图,矩形 的对角线 , 交于点 ,且 , ,连接 .求证: .
(1)、求嘉淇走到十字道口 向北走的概率;(2)、补全图2的树状图,并分析嘉淇经过两个十字道口后向哪个方向参观的概率较大.23. 如图,矩形 的对角线 , 交于点 ,且 , ,连接 .求证: .