山东省青岛市胶州市2021-2022学年九年级上学期期中数学试题
试卷更新日期:2021-12-08 类型:期中考试
一、单选题
-
1. 下列各组中的四条线段成比例的是( )A、1,1,2,3 B、1,2,3,4 C、2,3,4,5 D、2,3,6,92. 下列式子是一元二次方程的是( )A、 B、 C、 D、3. “十一”长假期间,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动,顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据:
转动转盘的次数n
100
150
200
500
800
1000
落在“铅笔”区域的次数m
68
108
140
355
560
690
落在“铅笔”区域的频率
0.68
0.72
0.70
0.71
0.70
0.69

下列说法错误的是( )
A、转动转盘20次,一定有6次获得“文具盒”铅笔文具盒 B、转动转盘一次,获得“铅笔”的概率大约是0.70 C、再转动转盘100次,指针落在“铅笔”区域的次数不一定是68次 D、如果转动转盘3000次,指针落在“文具盒”区域的次数大约有900次4. 如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开,若测得 km, km,则M,C两点之间的距离为( )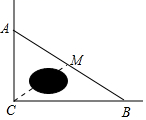 A、10km B、12km C、13km D、26km5. 如图,在平行四边形ABCD中,EF//AB交AD于点E,交BD于点F, , ,则CD的长为( )
A、10km B、12km C、13km D、26km5. 如图,在平行四边形ABCD中,EF//AB交AD于点E,交BD于点F, , ,则CD的长为( )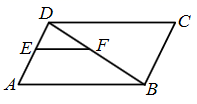 A、12 B、7 C、4 D、36. 定义运算: .例如 .则方程 的根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、只有一个实数根7. 如图,点O为矩形ABCD的对称中心,点E从点A出发沿AB向点B运动,移动到点B停止,延长EO交CD于点F,则四边形AECF形状的变化依次为( )
A、12 B、7 C、4 D、36. 定义运算: .例如 .则方程 的根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、只有一个实数根7. 如图,点O为矩形ABCD的对称中心,点E从点A出发沿AB向点B运动,移动到点B停止,延长EO交CD于点F,则四边形AECF形状的变化依次为( )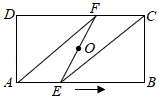 A、平行四边形→正方形→平行四边形→矩形 B、平行四边形→菱形→平行四边形→矩形 C、平行四边形→正方形→菱形→矩形 D、平行四边形→菱形→正方形→矩形8. 如图,在 中, ,以其三边为边向外作正方形,延长EA交BG于点M,连接IM交BC于点N,若M是BG的中点,则 的值是( )
A、平行四边形→正方形→平行四边形→矩形 B、平行四边形→菱形→平行四边形→矩形 C、平行四边形→正方形→菱形→矩形 D、平行四边形→菱形→正方形→矩形8. 如图,在 中, ,以其三边为边向外作正方形,延长EA交BG于点M,连接IM交BC于点N,若M是BG的中点,则 的值是( )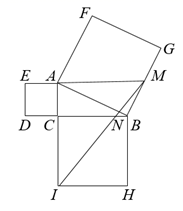 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 在学校举办的“美德少年”评选活动中,九年级一班有甲,乙,丙,丁共4名学生获奖.班主任决定在这4名获奖学生中随机选出2名学生在班级进行主题演讲,则甲被选中的概率为 .10. 如图,C,D是线段AB的两个黄金分割点,且 ,则线段CD的长为米.
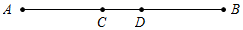 11. 某厂家2020年1~5月份的口罩产量统计如图所示,设从2月份到4月份,该厂家口罩产量的月平均增长率为 ,根据题意可得方程 .
11. 某厂家2020年1~5月份的口罩产量统计如图所示,设从2月份到4月份,该厂家口罩产量的月平均增长率为 ,根据题意可得方程 .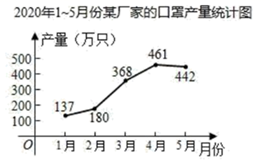 12. 如图,在△ABC中, , , ,则AC= .
12. 如图,在△ABC中, , , ,则AC= .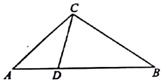 13. 如图在菱形 中, 是对角线 上一动点过点 作 于 . 于点 .若菱形 的周长为 ,面积为 ,则 的值为 .
13. 如图在菱形 中, 是对角线 上一动点过点 作 于 . 于点 .若菱形 的周长为 ,面积为 ,则 的值为 .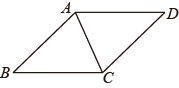 14. 如图,已知直线 ,过点 作x轴的垂线交直线l于点 ,以 为边作正方形 ,过点 作x轴的垂线交直线l于点 ,以 为边作正方形 ,…;则点 的坐标为.
14. 如图,已知直线 ,过点 作x轴的垂线交直线l于点 ,以 为边作正方形 ,过点 作x轴的垂线交直线l于点 ,以 为边作正方形 ,…;则点 的坐标为.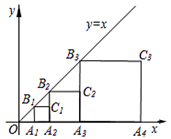
三、解答题
-
15. 已知如图,线段a.
求作:菱形ABCD,使该菱形边长和其中一条对角线长都为a.
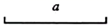 16.(1)、用配方法解方程: ;(2)、若关于x的一元二次方程 有一个解为 ,求k的值.17. 如图,四边形ABCD的对角线互相平分,请你添加一个条件使之变为菱形,并说明理由.
16.(1)、用配方法解方程: ;(2)、若关于x的一元二次方程 有一个解为 ,求k的值.17. 如图,四边形ABCD的对角线互相平分,请你添加一个条件使之变为菱形,并说明理由.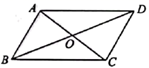 18. 有一个可自由转动的转盘,被分成了三个大小相同的扇形,分别标有数字2,4,6;另有一个不透明的瓶子,装有分别标有数字1,3,5的三个完全相同的小球.小明先转动一次转盘,停止后记下指针指向的数字(若指针指在分界线上则重转),小刚再从瓶子中随机取出一个小球,记下小球上的数字.若得到的两数字之和是3的倍数,则小明赢;若得到的两数字之和是7的倍数,则小刚赢,你认为这个游戏公平吗?请说明理由.
18. 有一个可自由转动的转盘,被分成了三个大小相同的扇形,分别标有数字2,4,6;另有一个不透明的瓶子,装有分别标有数字1,3,5的三个完全相同的小球.小明先转动一次转盘,停止后记下指针指向的数字(若指针指在分界线上则重转),小刚再从瓶子中随机取出一个小球,记下小球上的数字.若得到的两数字之和是3的倍数,则小明赢;若得到的两数字之和是7的倍数,则小刚赢,你认为这个游戏公平吗?请说明理由.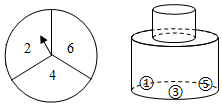 19. 某小区在绿化工程中有一块长为 ,宽为 的矩形空地,计划在其中修建两块相同的矩形绿地,使它们的面积之和为 ,两块绿地之间及周边留有宽度相等的人行通道(如图所示),求人行通道的宽度.
19. 某小区在绿化工程中有一块长为 ,宽为 的矩形空地,计划在其中修建两块相同的矩形绿地,使它们的面积之和为 ,两块绿地之间及周边留有宽度相等的人行通道(如图所示),求人行通道的宽度. 20. 如图,在 中, ,D为AC延长线上一点, , ,过点D作DE//AB交BC的延长线于点E.
20. 如图,在 中, ,D为AC延长线上一点, , ,过点D作DE//AB交BC的延长线于点E.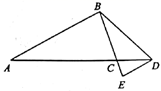 (1)、求证: ;(2)、求DE的长度.21. 已知:如图,在▱ABCD中,点E是BC的中点,连接AE并延长交DC的延长线于点F,连接BF.
(1)、求证: ;(2)、求DE的长度.21. 已知:如图,在▱ABCD中,点E是BC的中点,连接AE并延长交DC的延长线于点F,连接BF.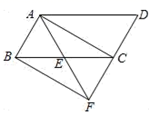 (1)、求证:△ABE≌△FCE;(2)、若AF=AD,判断四边形ABFC的形状,并说明理由.22. 在“乡村振兴”行动中,某村办企业开发了一种成本价为50元/盒的有机产品,如果每盒的售价为60元时,每天可以销售200盒,通过市场调查发现,每盒售价每提高1元,每天少卖出10盒.该村办企业要想每天获得2240元利润,该有机产品的售价可以定为多少元/盒?23. 问题提出:
(1)、求证:△ABE≌△FCE;(2)、若AF=AD,判断四边形ABFC的形状,并说明理由.22. 在“乡村振兴”行动中,某村办企业开发了一种成本价为50元/盒的有机产品,如果每盒的售价为60元时,每天可以销售200盒,通过市场调查发现,每盒售价每提高1元,每天少卖出10盒.该村办企业要想每天获得2240元利润,该有机产品的售价可以定为多少元/盒?23. 问题提出:将正m边形( )不断向外扩展,每扩展一个,正m边形每条边上的点的个数(以下简称“点数”)就增加一个,则n个正m边形的点数总共有多少个?
问题探究:
为了解决上面的问题,我们将采取一般问题特殊化的策略,先从简单和具体的情形入手:
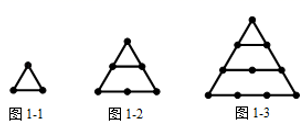
探究一:n个正三角形的点数总共有多少个?
如图1-1,1个正三角形的点数总共有 个;
如图1-2,2个正三角形的点数总共有 个;
如图1-3,3个正三角形的点数总共有 个;
……
n个正三角形的点数总共有 个.
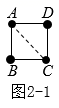
探究二:n个正四边形的点数总共有多少个?
如图2-1,连接AC,得到两个三角形△ABC和△ADC,这两个三角形相同之处在于,BC边与CD边都有相同个数的点,即2个点.每个三角形都有3个点,两个三角形就是 个点,因为这两个三角形在AC上有2个点重合,所以1个正四边形的点数总共有 (个);
如图2-2,连接AC,得到两个三角形△ABC和△ADC,这两个三角形相同之处在于,BC边与CD边都有相同个数的点,即3个点,每个三角形都有6个点,两个三角形就是 个点,因为这两个三角形在AC上有3个点重合,所以2个正四边形的点数总共有 (个);
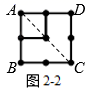
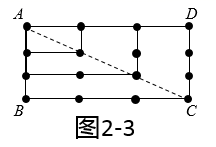
如图2-3,连接AC,得到两个三角形△ABC和△ADC,这两个三角形相同之处在于,BC边与CD边都有相同个数的点,即4个点.每个三角形都有10个点,两个三角形就是 个点,因为这两个三角形在AC上有4个点重合,所以3个正四边形的点数总共有 (个);
……
n个正四边形的点数总共有 ,即 个.
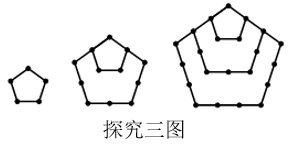
探究三:n个正五边形的点数总共有多少个?
类比探究二的方法:
1个正五边形的点数总共有5个;
2个正五边形的点数总共有12个;
3个正五边形的点数总共有个;
……
n个正五边形的点数总共有个.
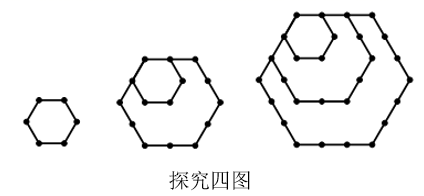
探究四:n个正六边形的点数总共有个.
问题解决:
n个正m边形的点数总共有个.
实际应用:
若9个正m边形的点数总共有820个,则m的值为 .
 24. 如图,四边形ABCD中,AD//BC, , , ,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.当其中一个动点到达终点时,另一个动点也随之停止运动.过点N作 于点P,连接AC交NP于点Q,连接MQ,设运动时间为t秒( )
24. 如图,四边形ABCD中,AD//BC, , , ,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.当其中一个动点到达终点时,另一个动点也随之停止运动.过点N作 于点P,连接AC交NP于点Q,连接MQ,设运动时间为t秒( )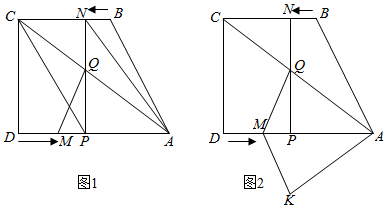 (1)、连接AN,CP,当t为何值时,四边形ANCP为平行四边形;(2)、设四边形DMQC的面积为y,求y与t的函数关系式;(3)、在运动过程中,是否存在某一时刻t,使四边形DMQC的面积与△ABC的面积相等?若存在,求出t的值;若不存在,请说明理由;(4)、将△AQM沿AD翻折,得到△AKM.在运动过程中,是否存在某时刻t,使四边形AQMK为菱形,若存在,求出t的值;若不存在,请说明理由.
(1)、连接AN,CP,当t为何值时,四边形ANCP为平行四边形;(2)、设四边形DMQC的面积为y,求y与t的函数关系式;(3)、在运动过程中,是否存在某一时刻t,使四边形DMQC的面积与△ABC的面积相等?若存在,求出t的值;若不存在,请说明理由;(4)、将△AQM沿AD翻折,得到△AKM.在运动过程中,是否存在某时刻t,使四边形AQMK为菱形,若存在,求出t的值;若不存在,请说明理由.