山东省聊城市东昌府区2021-2022学年九年级上学期期中数学试题

试卷更新日期：2021-12-08 类型：期中考试

进入出卷网下载

一、单选题

1. 在Rt△ABC中，∠A=90 $°$ ，AB=3，BC=4，则cosB=（）

A、 $\frac{3}{4}$ B、 $\frac{\sqrt{7}}{4}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
2. 已知△ABC，D，E分别在AB，AC边上，且DE∥BC，AD=2，DB=3，△ADE面积是4则四边形DBCE的面积是（）

A、6 B、9 C、21 D、25

查看试题解析
3. 如图，⊙O是△ABC的外接圆，∠OCB＝40°，则∠A的大小为（）

A、40° B、50° C、80° D、100°

查看试题解析
4. 如图所示，每个小正方形的边长均为1，则下列A、B、C、D四个图中的3三角形（阴影部分）与 $△ E F G$ 相似的是（）．

A、 B、 C、 D、

查看试题解析
5. 如图，AB是⊙O的直径，点D在AB的延长线上，DC切⊙O于点C，若∠A=25°，则∠D等于（）

A、20° B、30° C、40° D、50°

查看试题解析
6. 如图， $△ A B O$ 缩小后变为 $△ A^{'} B^{'} O$ ，其中 $A$ 、 $B$ 的对应点分别为 $A^{'}$ 、 $B^{'}$ ， $A^{'}$ 、 $B^{'}$ 均在图中格点上，若线段 $A B$ 上有一点 $P (m ， n)$ ，则点 $P$ 在 $A^{'} B^{'}$ 上的对应点 $P^{'}$ 的坐标为（）

A、 $(\frac{m}{2} ， n)$ B、 $(m ， n)$ C、 $(\frac{m}{2} ， \frac{n}{2})$ D、 $(m ， \frac{n}{2})$

查看试题解析
7. 如图所示，某拦水大坝的横断面为梯形ABCD，AE，DF为梯形的高，其中迎水坡AB的坡角α=45°，坡长 $A B = 10 \sqrt{2}$ 米，背水坡CD的坡度 $i = 1 ： \sqrt{3}$ ，则背水坡的坡长CD为（）米．

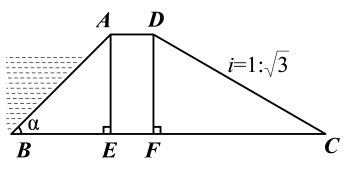A、20 B、 $20 \sqrt{3}$ C、10 D、 $20 \sqrt{2}$

查看试题解析
8. 图1是一个地铁站入口的双翼闸机．如图2，它的双翼展开时，双翼边缘的端点A与B之间的距离为10cm，双翼的边缘AC＝BD＝54cm，且与闸机侧立面夹角∠PCA＝∠BDQ＝30°．当双翼收起时，可以通过闸机的物体的最大宽度为（）

A、(54 $\sqrt{3}$ +10) cm B、(54 $\sqrt{2}$ +10) cm C、64 cm D、54cm

查看试题解析
9. 如图， $B C$ 是半圆 $O$ 的直径， $D$ ， $E$ 是 $\overset{⌢}{B C}$ 上两点，连接 $B D$ ， $C E$ 并延长交于点 $A$ ，连接 $O D$ ， $O E$ ，如果 $∠ A ＝ 70 °$ ，那么 $∠ D O E$ 的度数为（）

A、 $35 °$ B、 $38 °$ C、 $40 °$ D、 $42 °$

查看试题解析
10. 构造几何图形解决代数问题是“数形结合思想”的重要应用，小康在计算 $\tan 22.5 °$ 时，构造出如图所示的图形：在Rt $△$ ACD中， $∠ C = 90 °$ ， $∠ A B C = 45 °$ ，延长 $C B$ 到 $D$ ， $B D = A B$ ，连接 $A D$ ，得 $∠ D = 22.5 °$ ．根据此图可求得 $\tan 22.5 °$ 的结果（）

A、 $2 - \sqrt{3}$ B、 $\sqrt{2} + 1$ C、 $\sqrt{2} - 1$ D、 $2 - \sqrt{2}$

查看试题解析
11. 如图， $Δ A B C$ 中， $∠ A C B = 90 °$ ， $∠ B = 30 °$ ， $A C = 1$ ，过点 $C$ 作 $C D_{1} ⊥ A B$ 于 $D_{1}$ ，过点 $D_{1}$ 作 $D_{1} D_{2} ⊥ B C$ 于 $D_{2}$ ，过点 $D_{2}$ 作 $D_{2} D_{3} ⊥ A B$ 于 $D_{3}$ ，这样继续作下去，线段 $D_{n} D_{n + 1}$ （ $n$ 为正整数）等于（）.

A、 ${(\frac{1}{2})}^{n + 1}$ B、 ${(\frac{3}{2})}^{n + 1}$ C、 ${(\frac{\sqrt{3}}{2})}^{n}$ D、 ${(\frac{\sqrt{3}}{2})}^{n + 1}$

查看试题解析

二、多选题

12. 如图，在△ABC中，点P为AB上一点，给出下列四个条件中能满足△APC和△ACB相似的条件是（）

A、∠ACP=∠B B、∠APC=∠ACB C、AC²=AP·AB D、AB·CP=AP·CB

查看试题解析

三、填空题

13. 在△ABC中，若∠A ， ∠B满足|cosA－ $\frac{1}{2}$ |＋(sinB－ $\frac{\sqrt{2}}{2}$ )²＝0，则∠C＝．

查看试题解析
14. 如图，边长为1的小正方形网格中，⊙O的圆心在格点上，则∠AED的余弦值是．

查看试题解析
15. 如图所示，AB，AC与⊙O相切于点B，C，∠A=50°，点P是圆上异于B，C的一动点，则∠BPC的度数是．

查看试题解析
16. 轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行，在B处观测灯塔A位于南偏东75°方向上，轮船航行半小时到达C处，在C处观测灯塔A位于北偏东60°方向上，则B处与灯塔A的距离是海里．

查看试题解析
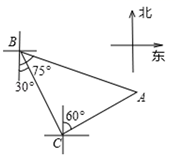17. 将三角形纸片(△ABC)按如图所示的方式折叠，使点B落在边AC上，记为点B′，折痕为EF．已知AB＝AC＝3，BC＝4，若以点B′，F，C为顶点的三角形与△ABC相似，则BF的长度是．

查看试题解析

四、解答题

18. 计算题

(1)、 $\cos^{2} 45 ° - 4 \sin 30 ° + {(\frac{1}{7})}^{- 1} - {(π - 3.14)}^{0}$ ；

(2)、已知 $α$ 是锐角，且 $\sin (α + 15 °) = \frac{\sqrt{3}}{2}$ ，计算 $\sqrt{8} - 4 \cos α - | 1 - 2 \sin α | + \tan α$ 的值．

查看试题解析
19. 已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A（0，3）、B（3，4）、C（2，2）（正方形网格中每个小正方形的边长是一个单位长度）．

⑴画出△ABC向下平移4个单位长度得到的△A₁B₁C₁ ，点C₁的坐标是 ▲ ；

⑵以点B为位似中心，在网格内画出△A₂B₂C₂ ，使△A₂B₂C₂与△ABC位似，且位似比为2：1，点C₂的坐标是 ▲ ；

⑶△A₂B₂C₂的面积是 ▲ 平方单位．

查看试题解析
20. 如图，已知 $Δ A B C$ 中， $∠ A B C = 30 ° ， ∠ A C B = 45 °$ ， $A B = 8$ .求 $Δ A B C$ 的面积.

查看试题解析
21. 如图，矩形 $A B C D$ 中， $E$ 为 $B C$ 上一点， $D F ⊥ A E$ 于点 $F$ ．

(1)、证明 $△ A B E ∽ △ D F A$ ；

(2)、若 $A B = 3$ ， $A D = 6$ ， $B E = 4$ ，求 $D F$ 的长．

查看试题解析
22. 如图，学校教学楼上悬挂一块长为3m的标语牌，即CD=3m，数学活动课上，小明和小红要测量标语牌的底部点D到地面的距离．测角仪支架高AE=BF=1.2m，小明在E处测得标语牌底部点D的仰角为31°，小红在 $F$ 处测得标语牌顶部点C的仰角为45°，AB=5m，依据他们测量的数据能否求出标语牌底部点D到地面的距离DH的长？（结果保留1位小数）（参考数据： $\tan 31 ° \approx 0.60 ， \sin 31 ° \approx 0.52 ， \cos 31 ° \approx 0.86$ ）

查看试题解析
23. 如图，BD是圆O的直径，A、C是圆O上的两个点，且AB=AC，AD与BC的延长线交于点E．

(1)、证明： $△$ ABD∽ $△$ AEB；

(2)、若AD=1，DE=3，求圆O的直径的长．

查看试题解析
24. 已知：如图，AC⊙O是的直径，BC是⊙O的弦，点P是⊙O外一点，∠PBA=∠C．

(1)、求证：PB是⊙O的切线；

(2)、若OP∥BC，且OP=8，BC=2．求⊙O的半径．

查看试题解析