山东省滨州市阳信县2021-2022学年九年级上学期期中数学试题
试卷更新日期:2021-12-08 类型:期中考试
一、单选题
-
1. 若⊙O的半径为4cm,点A到圆心O的距离为3cm,那么点A与⊙O的位置关系( )A、点A在圆内 B、点A在圆上 C、点A在圆外 D、不能确定2. 如图,点A、B、C是⊙O上的三个点,若∠AOB=82°,则∠C的度数为( )
 A、82° B、38° C、24° D、41°3. 一个不透明的袋子中有2个红球,3个黄球和4个蓝球,这些球除颜色外完全相同,从袋子中随机摸出一个球,它是红球的概率为( )A、 B、 C、 D、4. 下列事件中,属于必然事件的是( )A、购买一张彩票,中奖 B、射击运动员射击一次,命中10环 C、任意画一个三角形,内角和为 D、在一个只装有白球的袋中摸出红球5. 下列图形中的角是圆周角的是( )A、
A、82° B、38° C、24° D、41°3. 一个不透明的袋子中有2个红球,3个黄球和4个蓝球,这些球除颜色外完全相同,从袋子中随机摸出一个球,它是红球的概率为( )A、 B、 C、 D、4. 下列事件中,属于必然事件的是( )A、购买一张彩票,中奖 B、射击运动员射击一次,命中10环 C、任意画一个三角形,内角和为 D、在一个只装有白球的袋中摸出红球5. 下列图形中的角是圆周角的是( )A、 B、
B、 C、
C、 D、
D、 6. 如图,在平面直角坐标系中,将点 绕原点 逆时针旋转90°得到点 ,则 的坐标为( )
6. 如图,在平面直角坐标系中,将点 绕原点 逆时针旋转90°得到点 ,则 的坐标为( ) A、 B、 C、 D、7. 随着人们健康生活理念的提高,环保意识也不断增强,以下是回收、绿色包装、节水、低碳四个标志,其中是中心对称图形的是( )A、
A、 B、 C、 D、7. 随着人们健康生活理念的提高,环保意识也不断增强,以下是回收、绿色包装、节水、低碳四个标志,其中是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 8. 已知 是半径为6的圆的一条弦,则 的长不可能是( )A、8 B、10 C、12 D、149. 下列语句中,一定正确的是( )
8. 已知 是半径为6的圆的一条弦,则 的长不可能是( )A、8 B、10 C、12 D、149. 下列语句中,一定正确的是( )①过三点有且只有一个圆;②平分弦的直径垂直于弦;③三角形的外心到三角形三个顶点的距离相等;④同弧或等弧所对的圆周角相等;⑤圆内接平行四边形是矩形.
A、①②③ B、①②④ C、②③⑤ D、③④⑤10. 如图,AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,若∠A=25°,则∠D等于( ) A、20° B、30° C、40° D、50°11. 点 关于原点O的对称点 的坐标是( )A、 B、 C、 D、12. 如图,从圆外一点P引圆的两条切线PA,PB,A,B为切点,C为PB上的一点,连接CO交⊙O于点D,若 , , ,则⊙O的半径长是( )
A、20° B、30° C、40° D、50°11. 点 关于原点O的对称点 的坐标是( )A、 B、 C、 D、12. 如图,从圆外一点P引圆的两条切线PA,PB,A,B为切点,C为PB上的一点,连接CO交⊙O于点D,若 , , ,则⊙O的半径长是( )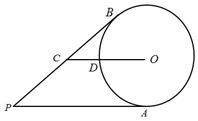 A、 B、 C、4 D、3
A、 B、 C、4 D、3二、填空题
-
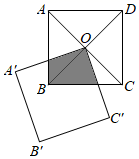
13. 如图,正方形 的对角线相交于点 ,点 是正方形 的一个顶点,如果两个正方形的边长相等,正方形 绕点 自由转动,设两个正方形重叠部分(阴影)的面积为 ,正方形 的面积为 .则 与 的关系是 .
 14. 弦心距:圆心到的距离(即圆心到弦的垂线段的距离).
14. 弦心距:圆心到的距离(即圆心到弦的垂线段的距离).在直角三角形中,由勾股定理得:2+半弦2=半径2
 15. 如图,若以AB为边长作⊙O的内接正多边形,则这个多边形是正边形.
15. 如图,若以AB为边长作⊙O的内接正多边形,则这个多边形是正边形.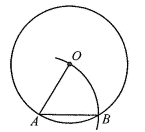 16. 如图,在△AOB中,AO=1,BO=AB= .将△AOB绕点O逆时针方向旋转90°,得到△A′OB′,连接AA′.则线段AA′的长为 .
16. 如图,在△AOB中,AO=1,BO=AB= .将△AOB绕点O逆时针方向旋转90°,得到△A′OB′,连接AA′.则线段AA′的长为 . 17. 数据分析技术为打赢疫情防控阻击战发挥了重要作用,如图是小明同学的健康码(绿码)示意图,用黑白打印机打印于边长为 的正方形区域内.为了估计图中黑色部分的总面积,在正方形区域内随机掷点,经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,估计黑色部分的总面积约为 .
17. 数据分析技术为打赢疫情防控阻击战发挥了重要作用,如图是小明同学的健康码(绿码)示意图,用黑白打印机打印于边长为 的正方形区域内.为了估计图中黑色部分的总面积,在正方形区域内随机掷点,经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,估计黑色部分的总面积约为 . 18. 已知⊙O的半径为10cm,AB,CD是⊙O的两条弦, , , ,则弦AB和CD之间的距离是 .
18. 已知⊙O的半径为10cm,AB,CD是⊙O的两条弦, , , ,则弦AB和CD之间的距离是 .三、解答题
-
19. 如图,方格纸中有三个格点 , , ,要求作一个多边形使这三个点在这个多边形的边(包括顶点)上,且多边形的顶点在方格的顶点上.
 (1)、在图甲中作一个三角形是轴对称图形;(2)、在图乙中作一个四边形是中心对称图形但不是轴对称图形;(3)、在图丙中作一个四边形既是轴对称图形又是中心对称图形.(注:图甲、图乙、图丙在答题纸上)20. 如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切于点C时,另一边与圆两个交点A和B的读数恰好为“2”和“8”(单位:cm)求该圆的半径.
(1)、在图甲中作一个三角形是轴对称图形;(2)、在图乙中作一个四边形是中心对称图形但不是轴对称图形;(3)、在图丙中作一个四边形既是轴对称图形又是中心对称图形.(注:图甲、图乙、图丙在答题纸上)20. 如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切于点C时,另一边与圆两个交点A和B的读数恰好为“2”和“8”(单位:cm)求该圆的半径. 21. 如图,在边长为1的正方形组成的网格中建立直角坐标系, 的顶点均在格点上,点O为原点,点A、B的坐标分别是 、 .
21. 如图,在边长为1的正方形组成的网格中建立直角坐标系, 的顶点均在格点上,点O为原点,点A、B的坐标分别是 、 . (1)、将 向下平移2个单位后得到 ,则点 的坐标为;(2)、将 绕点O逆时针旋转 后得到 ,请在图中作出 ,并求出这时点 的坐标为 ▲ ;(3)、在(2)中的旋转过程中,求线段OB扫过的图形的面积.22. 如图, 和 是⊙ 的两条切线,A,B是切点.C是 上任意一点,过点C画⊙ 的切线,分别交 和 于D,E两点,已知 ,求 的周长.
(1)、将 向下平移2个单位后得到 ,则点 的坐标为;(2)、将 绕点O逆时针旋转 后得到 ,请在图中作出 ,并求出这时点 的坐标为 ▲ ;(3)、在(2)中的旋转过程中,求线段OB扫过的图形的面积.22. 如图, 和 是⊙ 的两条切线,A,B是切点.C是 上任意一点,过点C画⊙ 的切线,分别交 和 于D,E两点,已知 ,求 的周长. 23. 为倡导“低碳出行”,每年9月22日为世界无车日,2020年9月22日,由中国城市公共交通协会联合清华大学中国城市研究院共同举办的第十四届“922绿色出行日”主题活动拉开序幕,环保部门对某城市居民出行使用交通方式的情况进行了问卷调查,将收回的问卷调查结果整理后,绘制了如下不完整的统计图,其中“骑自行车、电动车”所在的扇形的圆心角是162°.
23. 为倡导“低碳出行”,每年9月22日为世界无车日,2020年9月22日,由中国城市公共交通协会联合清华大学中国城市研究院共同举办的第十四届“922绿色出行日”主题活动拉开序幕,环保部门对某城市居民出行使用交通方式的情况进行了问卷调查,将收回的问卷调查结果整理后,绘制了如下不完整的统计图,其中“骑自行车、电动车”所在的扇形的圆心角是162°.
请根据以上信息解答下列问题:
(1)、请补全条形统计图.(2)、如果绿色出行是指“骑自行车、电动车”和“坐公交车”,计算绿色出行在所有交通方式中的频率,并在50万人口的城市中选择绿色出行的共有多少人.(3)、若参与问卷调查的人中选择“其他”交通方式的有两名女性,其余为男性,现从中随机选取两人进行跟踪调查,请借助树状图或者表格,求出恰好选到1男1女的概率.24. 如图,在 中,经过A,B两点的⊙O与边BC交于点E,圆心O在BC上,过点O作 交⊙O于点D,连接AD交BC于点F,且 . (1)、试判断AC与⊙O的位置关系,并说明理由;(2)、若 , .求图中阴影部分的面积(结果保留 ).
(1)、试判断AC与⊙O的位置关系,并说明理由;(2)、若 , .求图中阴影部分的面积(结果保留 ).