吉林省长春市朝阳区2021-2022学年高二上学期数学期中考试试卷

试卷更新日期：2021-12-08 类型：期中考试

进入出卷网下载

一、单选题

1. 已知直线 $l$ 经过点 $A (1 + \sqrt{3} ， 3)$ ， $B (1 ， 4)$ ，则 $l$ 的倾斜角为（）

A、30° B、60° C、120° D、150°

查看试题解析
2. 若椭圆 $\frac{x^{2}}{m} + \frac{y^{2}}{3} = 1$ 的一个焦点为 $(0 ， - 1)$ ，则m的值为（）

A、4 B、3 C、2 D、1

查看试题解析
3. 如图，四面体 $O$ - $A B C$ ， $G$ 是底面△ $A B C$ 的重心， $\vec{O A} = \vec{a} ， \vec{O B} = \vec{b} ， \vec{O C} = \vec{c}$ ，则 $\vec{O G} =$ （）

A、 $\frac{1}{3} \vec{a} + \frac{2}{3} \vec{b} + \frac{2}{3} \vec{c}$ B、 $\frac{1}{3} \vec{a} + \frac{1}{3} \vec{b} + \frac{1}{3} \vec{c}$ C、 $\frac{2}{3} \vec{a} + \frac{2}{3} \vec{b} + \frac{2}{3} \vec{c}$ D、 $\frac{2}{3} \vec{a} + \frac{2}{3} \vec{b} + \frac{1}{3} \vec{c}$

查看试题解析
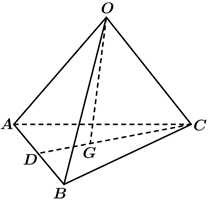4. 直线 $a x + b y + c = 0$ 经过一、三、四象限的充要条件是（）

A、 $a b > 0$ ， $b c > 0$ B、 $a b < 0$ ， $b c > 0$ C、 $a b > 0$ ， $b c < 0$ D、 $a b < 0$ ， $b c < 0$

查看试题解析
5. 已知圆 $M ： x^{2} + y^{2} - 2 a y = 0$ （ $a > 0$ ）截直线 $x + y = 0$ 所得线段的长度为 $2 \sqrt{2}$ ，则圆 $M$ 与圆 $N ： x^{2} + y^{2} - 6 x - 12 y - 4 = 0$ 的位置关系是（）

A、内切 B、外切 C、相交 D、相离

查看试题解析
6. 已知圆 $x^{2} + y^{2} = 25$ 的一条弦经过点 $P (1 ， 3)$ ，当弦长最短时，该弦所在直线的方程为（）

A、 $3 x - y = 0$ B、 $2 x + y - 5 = 0$ C、 $x + 3 y - 10 = 0$ D、 $x + y - 4 = 0$

查看试题解析
7. 若 $y = a | x |$ 与 $y = x + a (a > 0)$ 的图形有两个交点，则 $a$ 的取值范围是（）

A、 $a > 1$ B、 $0 < a < 1$ C、 $\emptyset$ D、 $0 < a < 1$ 或 $a > 1$

查看试题解析
8. 已知点M，N分别在直线 $l_{1}$ ： $x + y = 0$ 与直线 $l_{2}$ ： $x + y - 3 = 0$ ，且 $M N ⊥ l_{1}$ ，点 $P (- 1 ， - 3)$ ， $Q (\frac{7}{2} ， \frac{1}{2})$ ，则 $| P M | + | Q N |$ |的最小值为（）

A、 $\frac{\sqrt{15}}{2}$ B、 $\sqrt{15}$ C、 $\sqrt{13}$ D、 $3 \sqrt{3}$

查看试题解析

二、多选题

9. 设 ${\vec{m} ， \vec{n} ， \vec{t}}$ 是空间的一组基底，则下列结论正确的是（）

A、基底 ${\vec{m} ， \vec{n} ， \vec{t}}$ 中的向量可以为任意向量. B、空间中任一向量 $\vec{a}$ ，存在唯一有序实数组 $(x ， y ， z)$ ，使 $\vec{a} = x \vec{m} + y \vec{n} + z \vec{t}$ C、若 $\vec{m} ⊥ \vec{n}$ ， $\vec{n} ⊥ \vec{t}$ ，则 $\vec{m} ⊥ \vec{t}$ D、 ${\vec{m} + 2 \vec{n} ， \vec{n} + 2 \vec{t} ， \vec{t} + 2 \vec{m}}$ 也可以构成空间的一组基底.

查看试题解析
10. 若直线 $x + a y - 2 = 0$ 与直线 $a^{2} x + y + 1 = 0$ 垂直，则 $a =$ （）

A、0 B、-1 C、0 D、1

查看试题解析
11. 已知Р是椭圆 $Γ$ ： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 上的一动点，离心率为e，椭圆与x轴的交点分别为A、B，左、右焦点分别为 $F_{1}$ 、 $F_{2}$ .下列关于椭圆的四个结论中正确的是（）

A、若PA、PB的斜率存在且分别为 $k_{1}$ 、 $k_{2}$ ，则 $k_{1} k_{2}$ 为一定值 B、根据光学现象知道：从 $F_{1}$ 发出的光线经过椭圆反射后一定会经过 $F_{2}$ .若一束光线从 $F_{1}$ 出发经椭圆反射，当光线第n次到达 $F_{2}$ 时，光线通过的总路程为4na C、若 $△ M F_{1} F_{2}$ 的面积最大时， $∠ F_{1} M F_{2} = 120 °$ ，则 $e = \frac{\sqrt{3}}{2}$ D、若椭圆C上存在点M使 $\vec{M F_{1}} \cdot \vec{M F_{2}} = 0$ ，则 $e \in (0 ， \frac{\sqrt{2}}{2})$

查看试题解析
12. 已知圆 $M ： {(x + 1)}^{2} + y^{2} = 2$ ， $(M$ 为圆心）直线 $l ： x - y - 3 = 0$ ，点 $P$ 在直线 $l$ 上运动，直线PA，PB分别于圆 $M$ 切于点 $A$ ， $B$ ．则下列说法正确的是（）

A、四边形 $P A M B$ 的面积最小值为 $2 \sqrt{3}$ B、 $| P A |$ 最短时，弦 $A B$ 长为 $\sqrt{6}$ C、 $| P A |$ 最短时，弦 $A B$ 直线方程为 $x - y - 1 = 0$ D、直线 $A B$ 过定点为 $(- \frac{1}{2}$ ， $- \frac{1}{2})$

查看试题解析

三、填空题

13. 已知圆 $x^{2} + y^{2} + a x + b y = 0$ 的圆心坐标 $(3 ， 4)$ ，则圆的半径是.

查看试题解析
14. 已知 $\vec{a} = (2 ， - 1 ， 0)$ ， $\vec{b} = (k ， 0 ， 1)$ ，若 $〈 \vec{a} ， \vec{b} 〉 = 120^{\circ}$ ，则 $k =$ .

查看试题解析
15. 如果实数x，y满足等式(x－1)²＋y²＝ $\frac{3}{4}$ ，那么 $\frac{y}{x}$ 的最大值是。

查看试题解析
16. 在如图所示的试验装置中，四边形框架 $A B C D$ 为正方形， $A B E F$ 为矩形，且 $B E = 3 A B = 3$ ，且它们所在的平面互相垂直， $N$ 为对角线 $B F$ 上的一个定点，且 $2 F N = B N$ ，活动弹子 $M$ 在正方形对角线 $A C$ 上移动，当 $\vec{M E} \cdot \vec{M N}$ 取最小值时，活动弹子 $M$ 到直线 $B F$ 的距离为.

查看试题解析

四、解答题

17. 已知直线l经过点 $(0 ， 2)$ ，其倾斜角为 $30^{°}$ .

(1)、求直线l的方程；

(2)、求直线l与两坐标轴围成的三角形的面积.

查看试题解析
18. 如图，在长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，底面ABCD是边长为1的正方形， $A A_{1} = 2$ ，点E，F分别为棱 $C C_{1}$ ， $A A_{1}$ 的中点.

(1)、求证： $D_{1} F / /$ 平面BDE；

(2)、求直线 $D_{1} F$ 到平面BDE的距离.

查看试题解析
19. 求解下列问题：

(1)、已知 $△ A O B$ 的三个顶点分别是点 $A (4 ， 0)$ ， $O (0 ， 0)$ ， $B (0 ， 3)$ ，求 $△ A O B$ 的外接圆的标准方程.

(2)、一圆经过点 $(- 2 ， - 4)$ ，且与直线 $x + 3 y - 26 = 0$ 相切于点 $(8 ， 6)$ ，试求该圆的标准方程.

查看试题解析
20. 在某海礁A处有一风暴中心，距离风暴中心A正东方向200km的B处有一艘轮船，正以北偏西a（a为锐角）角方向航行，速度为40km/h．已知距离风暴中心180km以内的水域受其影响．

(1)、若轮船不被风暴影响，求角α的正切值的最大值？

(2)、若轮船航行方向为北偏西45°，求轮船被风暴影响持续多少时间？

查看试题解析
21. 如图，在平行四边形 $A B C D$ 中， $A B = 1$ ， $A D = 2$ ， $∠ A B C = \frac{π}{3}$ ，四边形 $A C E F$ 为矩形，平面 $A C E F ⊥$ 平面 $A B C D$ ， $A F = 1$ ，点 $M$ 在线段 $E F$ 上运动，且 $\vec{E M} = λ \vec{E F}$ .

(1)、当 $λ = \frac{1}{2}$ 时，证明 $D E ⊥ B M$ ；

(2)、设平面 $M B C$ 与平面 $E C D$ 的夹角为 $θ$ ，求 $\cos θ$ 的取值范围.

查看试题解析
22. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 过点 $(\frac{\sqrt{2}}{2} ， \frac{\sqrt{3}}{2})$ ，椭圆的焦距为2．

(1)、求椭圆 $C$ 的方程；

(2)、设直线 $l$ 过点 $(0 ， - \frac{1}{2})$ ，且斜率为 $- \frac{1}{k} (k \neq 0)$ ，若椭圆 $C$ 上存在 $A ， B$ 两点关于直线 $l$ 对称， $O$ 为坐标原点，求 $k$ 的取值范围及 $△ A O B$ 面积的最大值．

查看试题解析