黑龙江省大庆市龙凤区2021-2022学年九年级上学期期中数学试题
试卷更新日期:2021-12-08 类型:期中考试
一、单选题
-
1. 二次函数 的图象的开口方向、对称轴、顶点坐标分别是( )A、向上、直线 , B、向上、直线 , C、向下、直线 , D、向下、直线 ,2. 抛物线 的图象经过点 , , ,则 , , 大小关系是( )A、 B、 C、 D、3. 如图,在 中,半径 于点D, ,则下列说法正确的是( )
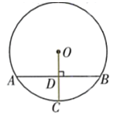 A、 B、 C、 D、AB垂直平分OC4. 点 关于原点的对称点 的坐标是( )A、 B、 C、 D、5. 在同一平面直角坐标中,直线y=ax+b与抛物线y=ax2+b的图象可能是( )A、
A、 B、 C、 D、AB垂直平分OC4. 点 关于原点的对称点 的坐标是( )A、 B、 C、 D、5. 在同一平面直角坐标中,直线y=ax+b与抛物线y=ax2+b的图象可能是( )A、 B、
B、 C、
C、 D、
D、 6. 矩形ABCD中,AB=8, ,点P在边AB上,且BP=3AP,如果圆P是以点P 为圆心,PD为半径的圆,那么下列判断正确的是( ).A、点B、C均在圆P外 B、点B在圆P外、点C在圆P内 C、点B在圆P内、点C在圆P外 D、点B、C均在圆P内7. 如图所示,在 中,斜边 , ,点D在AB上,且 ,则 的值是( )
6. 矩形ABCD中,AB=8, ,点P在边AB上,且BP=3AP,如果圆P是以点P 为圆心,PD为半径的圆,那么下列判断正确的是( ).A、点B、C均在圆P外 B、点B在圆P外、点C在圆P内 C、点B在圆P内、点C在圆P外 D、点B、C均在圆P内7. 如图所示,在 中,斜边 , ,点D在AB上,且 ,则 的值是( ) A、 B、1 C、 D、8. 如图,已知二次函数 向右平移2个单位得到抛物线 的图象,则阴影部分的面积为( )
A、 B、1 C、 D、8. 如图,已知二次函数 向右平移2个单位得到抛物线 的图象,则阴影部分的面积为( ) A、3 B、4 C、5 D、69. 如图, 是半圆 的直径, 为弦, 于 ,过点 作 交半圆 于点 ,过点 作 于 ,若 ,则 的长为( )
A、3 B、4 C、5 D、69. 如图, 是半圆 的直径, 为弦, 于 ,过点 作 交半圆 于点 ,过点 作 于 ,若 ,则 的长为( ) A、1 B、 C、2 D、410. 如图是抛物线y=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),有下列结论:①2a+b=0,②abc>0;③方程ax2+bx+c=3有两个相等的实数根,④当y<0时,﹣2<x<4,其中正确的是( )
A、1 B、 C、2 D、410. 如图是抛物线y=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),有下列结论:①2a+b=0,②abc>0;③方程ax2+bx+c=3有两个相等的实数根,④当y<0时,﹣2<x<4,其中正确的是( ) A、②③ B、①③ C、①③④ D、①②③④
A、②③ B、①③ C、①③④ D、①②③④二、填空题
-
11. 若 ,则锐角 °.12. 如图,在 中, , ,则 的度数为 .
 13. 如图,某高速公路建设中需要测量某条江的宽度AB,飞机上的测量人员在C处测得A,B两点的俯角分别为 和 若飞机离地面的高度CH为1200米,且点H,A,B在同一水平直线上,则这条江的宽度AB为米 结果保留根号 .
13. 如图,某高速公路建设中需要测量某条江的宽度AB,飞机上的测量人员在C处测得A,B两点的俯角分别为 和 若飞机离地面的高度CH为1200米,且点H,A,B在同一水平直线上,则这条江的宽度AB为米 结果保留根号 .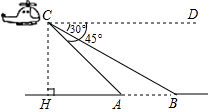 14. 已知 的半径为10,直线AB与 相交,则圆心O到直线AB距离d的取值范围是 .15. 如图,抛物线 与直线 交于 , 两点,则不等式 的解集是 .
14. 已知 的半径为10,直线AB与 相交,则圆心O到直线AB距离d的取值范围是 .15. 如图,抛物线 与直线 交于 , 两点,则不等式 的解集是 . 16. 如图,把抛物线 沿直线 平移 个单位后,其顶点在直线上的A处,则平移后抛物线的表达式是 .
16. 如图,把抛物线 沿直线 平移 个单位后,其顶点在直线上的A处,则平移后抛物线的表达式是 . 17. 如图,小明在距离地面30米的P处测得A处的俯角为15°,B处的俯角为60°.若斜面坡度为1: ,则斜坡AB的长是米.
17. 如图,小明在距离地面30米的P处测得A处的俯角为15°,B处的俯角为60°.若斜面坡度为1: ,则斜坡AB的长是米. 18. 如图,平面直角坐标系中,分别以点 , 为圆心,以1,3为半径作 , ,M,N分别是 , 上的动点,P为x轴上的动点,则 的最小值等于 .
18. 如图,平面直角坐标系中,分别以点 , 为圆心,以1,3为半径作 , ,M,N分别是 , 上的动点,P为x轴上的动点,则 的最小值等于 .
三、解答题
-
19. 计算:(1)、 ;(2)、 .20. 如图,正方形网格中有—段弧,弧上三点 , , 均在格点上.
 (1)、圆心 的坐标是(), .(2)、求 的长度.21. 如图,AB是 的直径, 于点E,连接CO并延长交AD于点F,且 .
(1)、圆心 的坐标是(), .(2)、求 的长度.21. 如图,AB是 的直径, 于点E,连接CO并延长交AD于点F,且 . (1)、求证:E是OB的中点;(2)、若 ,求CD的长.22. 如图,某煤矿因不按规定操作发生瓦斯爆炸,救援队立即赶赴现场进行救援,救援队利用生命探测仪在地面A,B两个探测点探测到地下C处有生命迹象.已知A,B两点相距8米,探测线与地面的夹角分别是30°和45°,试确定生命所在点C的深度(结果保留根号).
(1)、求证:E是OB的中点;(2)、若 ,求CD的长.22. 如图,某煤矿因不按规定操作发生瓦斯爆炸,救援队立即赶赴现场进行救援,救援队利用生命探测仪在地面A,B两个探测点探测到地下C处有生命迹象.已知A,B两点相距8米,探测线与地面的夹角分别是30°和45°,试确定生命所在点C的深度(结果保留根号). 23. 如图,已知二次函数 的图象经过A(2,0).
23. 如图,已知二次函数 的图象经过A(2,0). (1)、求 的值.(2)、若二次函数于 轴相交于的 点,且该二次函数的对称轴与 轴交于点 ,连结 ,求 的面积.24. 如图,在半径为5的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.
(1)、求 的值.(2)、若二次函数于 轴相交于的 点,且该二次函数的对称轴与 轴交于点 ,连结 ,求 的面积.24. 如图,在半径为5的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E. (1)、当BC=6时,求线段OD的长;(2)、在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度;如果不存在,请说明理由.25. 如图所示,小杰发现垂直地面的旗杆AB的影子落在地面和斜坡上,影长分别为BC和CD,经测量得 米, 米,斜坡CD的坡度为 ,且此时测得垂直于地面的1米长的标杆在地面上的影长为2米.求旗杆AB的长度.(结果保留整数,其中 )
(1)、当BC=6时,求线段OD的长;(2)、在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度;如果不存在,请说明理由.25. 如图所示,小杰发现垂直地面的旗杆AB的影子落在地面和斜坡上,影长分别为BC和CD,经测量得 米, 米,斜坡CD的坡度为 ,且此时测得垂直于地面的1米长的标杆在地面上的影长为2米.求旗杆AB的长度.(结果保留整数,其中 ) 26. 如图,在 中, ,AC、BC的长恰好为方程 的两根,且 ,D为AB的中点.
26. 如图,在 中, ,AC、BC的长恰好为方程 的两根,且 ,D为AB的中点. (1)、求a的值.(2)、动点P从点A出发,沿A→D→C的路线向点C运动;点Q从点B出发,沿B→C的路线向点C运动.若点P、Q同时出发,速度都为每秒2个单位,当点P经过点D时,点P速度变为每秒3单位,同时点Q速度变为每秒1个单位.当其中有一点到达终点时整个运动随之结束.设运动时间为t秒.在整个运动过程中,设 的面积为S,试求S与t之间的函数关系式;并指出自变量t的取值范围.27. 某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=-x+60(30≤x≤60).设这种双肩包每天的销售利润为w元.
(1)、求a的值.(2)、动点P从点A出发,沿A→D→C的路线向点C运动;点Q从点B出发,沿B→C的路线向点C运动.若点P、Q同时出发,速度都为每秒2个单位,当点P经过点D时,点P速度变为每秒3单位,同时点Q速度变为每秒1个单位.当其中有一点到达终点时整个运动随之结束.设运动时间为t秒.在整个运动过程中,设 的面积为S,试求S与t之间的函数关系式;并指出自变量t的取值范围.27. 某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=-x+60(30≤x≤60).设这种双肩包每天的销售利润为w元.
(1)、求w与x之间的函数解析式;
(2)、这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?(3)、如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
28. 如图,抛物线 与直线 相交于 , 两点,且抛物线经过点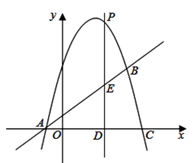 (1)、求抛物线的解析式.(2)、点P是抛物线上的一个动点(不与点 点 重合),过点P作直线 轴于点D,交直线AB于点E.当 时,求P点坐标;(3)、如图所示,设抛物线与 轴交于点F,在抛物线的第一象限内,是否存在一点Q,使得四边形OFQC的面积最大?若存在,请求出点Q的坐标;若不存在,说明理由.
(1)、求抛物线的解析式.(2)、点P是抛物线上的一个动点(不与点 点 重合),过点P作直线 轴于点D,交直线AB于点E.当 时,求P点坐标;(3)、如图所示,设抛物线与 轴交于点F,在抛物线的第一象限内,是否存在一点Q,使得四边形OFQC的面积最大?若存在,请求出点Q的坐标;若不存在,说明理由.