广东省揭阳市空港经济区2021-2022学年九年级上学期期中数学试题

试卷更新日期：2021-12-08 类型：期中考试

进入出卷网下载

一、单选题

1. 在抛掷一枚质地均匀的硬币的实验中，第100次抛掷时，反面朝上的概率是（）

A、 $\frac{1}{100}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、不确定

查看试题解析
2. 若 $\frac{y}{x}$ = $\frac{3}{4}$ ，则 $\frac{x + y}{x}$ 的值为（　　）

A、1 B、 $\frac{4}{7}$ C、 $\frac{5}{4}$ D、 $\frac{7}{4}$

查看试题解析
3. 观察下列表格，求一元二次方程x²﹣x=1.1的一个近似解是（　　）
       x
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
   x²﹣x
0.11
0.24
0.39
0.56
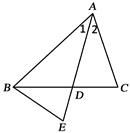
0.75
0.96
1.19
1.44
1.71

A、0.11 B、1.6 C、1.7   D、1.19

查看试题解析
4. 矩形、菱形、正方形都具有的性质是（）

A、对角线互相垂直 B、对角线相等 C、对角线互相平分 D、每一条对角线平分一组对角

查看试题解析
5. 如图，点P在△ABC的边AC上，要判断△ABP∽△ACB，添加一个条件，错误的是（）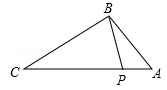

A、∠ABP=∠C B、∠APB=∠ABC C、 $\frac{A P}{A B} = \frac{A B}{A C}$ D、 $\frac{A B}{B P} = \frac{A C}{C B}$

查看试题解析
6. 一块四周镶有宽度相等的花边的地毯，如图所示，它的长为 8m，宽为 5m，如果地毯中央长方形图案的面积为 18m².则花边的宽是（）

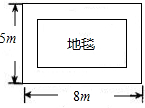A、2m B、1m C、1.5m D、0.5m

查看试题解析
7. 菱形的周长是24，两邻角的度数之比是1：2，那么较短的对角线的长是（）

A、3 B、5 C、6 D、6.5

查看试题解析
8. 有两组扑克牌各三张，牌面数字均为 $1$ ， $2$ ， $3$ ，随意从每组牌中各抽一张，数字之和等于 $4$ 的概率是（）

A、 $\frac{2}{9}$ B、 $\frac{1}{3}$ C、 $\frac{4}{9}$ D、 $\frac{5}{9}$

查看试题解析
9. 已知m，n为一元二次方程 $x^{2} - 4 x - 3 = 0$ 的两个实数根，则 $(m - 2) (n - 2)$ 的值为（）

A、-7 B、7 C、-2 D、2

查看试题解析
10. 如图，正方形ABCD中，点E，F分别在BC，CD上， $△ A E F$ 是等边三角形，连接AC交EF于G，下列结论：① $B E = D F$ ，② $∠ D A F = 15 °$ ，③AC垂直平分EF，④ $B E + D F = E F$ ．其中错误结论的是（）

A、① B、② C、③ D、④

查看试题解析

二、填空题

11. 关于x的方程 $(m - \sqrt{3}) x^{m^{2} - 1} - x + 3 = 0$ 是一元二次方程，则m= ．

查看试题解析
12. 已知正方形ABCD的对角线AC= $\sqrt{2}$ ，则正方形ABCD的周长为．

查看试题解析
13. 有四张大小、形状及背面完全相同的卡片，卡片正面分别画有等边三角形、正方形、平行四边形、菱形，从这四张卡片中任意抽取一张，卡片正面的图形既是轴对称图形又是中心对称图形的概率是．

查看试题解析
14. 如图是一位同学设计的用手电筒来测量某古城墙高度的示意图．点P处放一水平的平面镜，光线从点A出发经平面镜反射后刚好到古城墙CD的顶端C处，已知AB⊥BD，CD⊥BD，测得AB=2米，BP=3米，PD=12米，那么该古城墙的高度CD是米．

查看试题解析
15. 若关于x的一元二次方程kx²+2(k+1)x+k－1=0有两个实数根，则k的取值范围是．

查看试题解析
16. 如图，边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG，EF交AD于点H，那么DH的长是．

查看试题解析
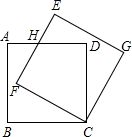17. 如图，菱形ABCD的对角线的长分别为2和5，P是对角线AC上任一点（点P不与点A、C重合），且PE∥BC交AB于E，PF∥CD交AD于F，则阴影部分的面积是．

查看试题解析

三、解答题

18. 用配方法解方程： $x^{2} - 2 x = 4$ ．

查看试题解析
19. 一只不透明的箱子里共有3个球，其中2个白球.1个红球，它们除颜色外均相同．从箱子中随机摸出一个球，记录下颜色后不将它放回箱子，搅匀后再摸出一个球．请你用列表或画树状图的方法，求两次摸出的球都是白球的概率．

查看试题解析
20. 如图，已知∠1=∠2，AB•AC=AD•AE．求证：∠C=∠E．

查看试题解析
21. 如图，已知 $A D$ ∥ $B E$ ∥ $C F$ ，它们依次交直线 $l_{1}$ 、 $l_{2}$ 于点 $A$ 、 $B$ 、 $C$ 和点 $D$ 、 $E$ 、 $F$ ， $\frac{D E}{E F} = \frac{2}{5}$ ， $A C = 14$ ；

(1)、求 $A B$ 、 $B C$ 的长；

(2)、如果 $A D = 7$ ， $C F = 14$ ，求 $B E$ 的长；

查看试题解析
22. 某种商品的标价为400元/件，经过两次降价后的价格为324元/件，并且两次降价的百分率相同．

(1)、求该种商品每次降价的百分率；

(2)、若该种商品进价为300元/件，两次降价共售出此种商品100件，为使两次降价销售的总利润不少于3210元．问第一次降价后至少要售出该种商品多少件？

查看试题解析
23. 如图，在△ABC中，点O是AC边上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的角平分线于点E，交∠BCA的外角平分线于点F．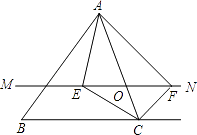

(1)、求证：EO=FO；

(2)、当点O运动到何处时，四边形AECF是矩形？并证明你的结论．

查看试题解析
24. 已知：如图，在矩形ABCD中，M，N分别是边AD，BC的中点，E，F分别是线段BM，CM的中点．

(1)、求证： $△ A B M ≌ △ D C M$ ；

(2)、判断四边形MENF是什么特殊四边形，并证明你的结论；

(3)、当AD，AB满足什么条件时，四边形MENF是正方形．

查看试题解析
25. 已知：平行四边形ABCD的两边AB、BC的长是关于x的方程 $x^{2} - (m + 3) x + 2 m + 2 = 0$ 的两个实数根．

(1)、试说明：无论m取何值方程总有两个实数根

(2)、当m为何值时，四边形ABCD是菱形？求出这时菱形的边长；

(3)、若AB的长为3，那么平行四边形ABCD的周长是多少？

查看试题解析

x	1.1	1.2	1.3	1.4	1.5	1.6	1.7	1.8	1.9
x²﹣x	0.11	0.24	0.39	0.56	0.75	0.96	1.19	1.44	1.71