辽宁省营口市大石桥市2021-2022学年八年级上学期期中数学试题
试卷更新日期：2021-12-08 类型：期中考试
一、单选题
-
1. 以下面各组线段为边，不能构成三角形的是（ ）A、5，6，7 B、6，6，6 C、8，4，4 D、20，30，362. 如图，一扇窗户打开后，用窗钩 可将其固定，这里所运用的几何原理是（ ）
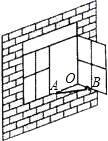A、三角形的稳定性 B、两点之间线段最短 C、两点确定一条直线 D、垂线段最短3. 已知一个多边形的内角和是1080°，则这个多边形是（ ）A、五边形 B、六边形 C、七边形 D、八边形4. 若点M(2，a)和点N(a+b，3)关于y轴对称，则a、b的值为（ ）A、a=3，b=－5 B、a=－3，b=5 C、a=3，b=5 D、a=－3，b=15. 如图，BE、CF是△ABC的角平分线，∠ABC=80°，∠A CB=60°，BE、CF相交 于D，则∠CDE的度数是（ ）
A、110° B、70° C、80° D、75°6. 下列运算正确的是 （ ）A、-a4·a3=a7 B、a4·a3=a12 C、(a4)3=a12 D、a4＋a3=a77. 如图，在△ABC中，AB＝AC，AD＝DE，∠BAD＝20°，∠EDC＝10°，则∠DAE的度数为（ ）
A、30° B、40° C、60° D、80°8. 如图，在等边 ABC中，AD是它的角平分线，DE⊥AB于E，若AC=8，则BE=（ ）
A、1 B、2 C、3 D、49. 如图，用直尺和圆规作已知角的平分线，要证明 成立的全等三角形的判定依据是（ ）
A、 B、 C、 D、10. 如图，已知等边 ABC，AB=2，点D在AB上，点F在AC的延长线上，BD=CF，DE⊥BC于E，FG⊥BC于G，DF交BC于点P，则下列结论：①BE=CG；② EDP≌ GFP；③∠EDP=60°；④EP=1中，一定正确的个数是（ ）个
A、1 B、2 C、3 D、4二、填空题
-
11. 若 ，则以a、b为边长的等腰三角形的周长为 ．12. 若am=3，则(a3)m= ．13. 如图，锐角△ABC的高AD、BE相交于F，若BF=AC，BC=7，CD=2，则AF的长为
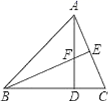14. 如图，在 中， ， ，AB的垂直平分线MN交AC于D点，连接BD ， 则 的度数是 ．
15. 如图，撑伞时，把伞“两侧的伞骨”和支架分别看作AB、AC和DB、DC，始终有AB=AC，DB=DC，请大家考虑一下伞杆AD所在的直线是B、C两点的连线BC的线．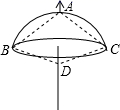
16. 如图，是A、B、C三个村庄的平面图，已知B村在A村的南偏西50°方向，C村在A村的南偏东15°方向，C村在B村的北偏东85°方向，求从C村村观测A、B两村的视角∠ACB的度数是 ．
三、解答题
-
17. 计算：(1)、[(-a)3]4；(2)、(-m2)3·(-m3)2 ．(3)、[(m-n)2]5(n-m)3(4)、(-x2)5+(-x5)218. 已知在△ABC中，AB＝AC，且线段BD为△ABC的中线，线段BD将△ABC的周长分成12和6两部分，求△ABC三边的长．
19. 如图，在边长为1个单位长度的小正方形组成的网格中，点A、B、C在小正方形的顶点上．
(1)、在图中画出与 ABC关于直线l成轴对称的(2)、四边形 的面积为；(3)、在直线l上找一点P，使PA+PB的长最短．20. 如图，AD⊥BC于D，AD=BD，AC=BE．
(1)、请说明∠1=∠C；(2)、猜想并说明DE和DC有何特殊关系．21. 如图在△ABC中，AB＝AC，∠BAC＝120°，EF为AB的垂直平分线，EF交BC于点F，交AB于点E.求证：BF＝ FC.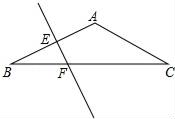
22.(1)、若2x+5y﹣3=0，求4x•32y的值．(2)、已知a3m=3，b3n=2．求（a2m）3+（bn）3-a2mbn·a4mb2n的值．23. 如图，已知AB＝CB，BE＝BF，点A，B，C在同一条直线上，∠1＝∠2.
(1)、证明：△ABE≌△CBF；(2)、若∠FBE＝40°，∠C＝45°，求∠E的度数．24. 已知点P在∠MON内．
(1)、如图1，点P关于射线OM的对称点是G，点P关于射线ON的对称点是H，连接OG、OH、OP．①若∠MON=50°，则∠GOH= ▲ ；
②若PO=5，连接GH，请说明当∠MON为多少度时，GH=10；
(2)、如图2，若∠MON=60°，A、B分别是射线OM、ON上的任意一点，当 PAB的周长最小时，求∠APB的度数．25. （阅读材料）小明同学发现这样一个规律：两个顶角相等的等腰三角形，如果具有公共的顶角的顶点，并把它们的底角顶点连接起来则形成一组全等的三角形，小明把具有这个规律的图形称为“手拉手”图形如图1，在“手拉手”图形中，小明发现若∠BAC=∠DAE，AB=AC，AD=AE，则 ABD≌ ACE．
(1)、（材料理解）
在图1中证明小明的发现．(2)、（深入探究）
如图2， ABC和 AED是等边三角形，连接BD，EC交于点O，连接AO，下列结论：①BD=EC；②∠BOC=60°；③∠AOE=60°，其中正确的有 ． (将所有正确的序号填在横线上）(3)、（延伸应用）
如图3，在四边形ABCD中，BD=CD，AB=BE，∠ABE=∠BDC=60°，试探究∠A与∠BED的数量关系，并证明．