2021-2022学年浙教版数学八年级上册期末检测卷1
试卷更新日期:2021-12-08 类型:期末考试
一、单选题
-
1. 下列图形中的曲线不能表示 是 的函数的是( )A、
 B、
B、 C、
C、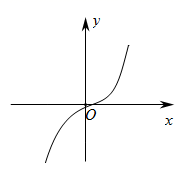 D、
D、 2. 若函数 是正比例函数,则 的值为( )A、 B、1 C、-1 D、23. 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若AB=8,△ABD的面积为16,则CD的长为( )
2. 若函数 是正比例函数,则 的值为( )A、 B、1 C、-1 D、23. 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若AB=8,△ABD的面积为16,则CD的长为( ) A、2 B、4 C、6 D、84. 如图,在△ABC和△ABD中,∠CAB=∠DAB,点A,B,E在同一条直线上,则添加以下条件,仍然不能判定△ABC≌△ABD的是( )
A、2 B、4 C、6 D、84. 如图,在△ABC和△ABD中,∠CAB=∠DAB,点A,B,E在同一条直线上,则添加以下条件,仍然不能判定△ABC≌△ABD的是( ) A、BC=BD B、∠C=∠D C、∠CBE=∠DBE D、AC=AD5. 如图,把含30°的直角三角板ABC绕点B顺时针旋转至如图△EBD,使BC在BE上,延长AC交DE于F,若AF=4,则AB的长为( )
A、BC=BD B、∠C=∠D C、∠CBE=∠DBE D、AC=AD5. 如图,把含30°的直角三角板ABC绕点B顺时针旋转至如图△EBD,使BC在BE上,延长AC交DE于F,若AF=4,则AB的长为( ) A、2 B、 C、 D、36. 下列条件中,不能判定△ABC是直角三角形的是( )A、a:b:c=5:12:13 B、b2=(a+c)(a﹣c) C、∠C=∠A﹣∠B D、∠A:∠B:∠C=3:4:57. 交通法规人人遵守,文明城市处处安全.在通过桥洞时,我们往往会看到如图所示的标志,这是限制车高的标志.则通过该桥洞的车高x(m)的范围在数轴上可表示为( )
A、2 B、 C、 D、36. 下列条件中,不能判定△ABC是直角三角形的是( )A、a:b:c=5:12:13 B、b2=(a+c)(a﹣c) C、∠C=∠A﹣∠B D、∠A:∠B:∠C=3:4:57. 交通法规人人遵守,文明城市处处安全.在通过桥洞时,我们往往会看到如图所示的标志,这是限制车高的标志.则通过该桥洞的车高x(m)的范围在数轴上可表示为( ) A、
A、 B、
B、 C、
C、 D、
D、 8. 随看科技的进步,我们可以通过手机APP实时查看公交车到站情况.小明想乘公交车,可又不想静静地等在A站.他从A站往B站走了一段路,拿出手机查看了公交车到站情况,发现他与公交车的距离为720m(如图),此时有两种选择:
8. 随看科技的进步,我们可以通过手机APP实时查看公交车到站情况.小明想乘公交车,可又不想静静地等在A站.他从A站往B站走了一段路,拿出手机查看了公交车到站情况,发现他与公交车的距离为720m(如图),此时有两种选择:
( 1 )与公交车相向而行,到A公交站去乘车;(2)与公交车同向而行,到B公交站去乘车.假设小明的速度是公交车速度的 ,若要保证小明不会错过这辆公交车,则A,B两公交站之间的距离最大为( )
A、240m B、300m C、320m D、360m9. 在平面直角坐标系xOy中,若点P在第四象限,且点P到x轴的距离为1,到y轴的距离为 ,则点P的坐标为( )A、( ) B、( ) C、( ) D、( )10. 在平面直角坐标系中,点 位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限二、填空题
-
11. 若不等式3x+a>2的解集是x>1,则a= .12. 如图在平面直角坐标系中,直线 与直线 交于点 ,C为直线 上一点,过点C作直线 轴于E,直线 交 于点D,当 时,则点 的坐标为.
 13. 将如图所示的“ ”笑脸放置在 的正方形网格中, 、 、 三点均在格点上.若 、 的坐标分别为 , ,则点 的坐标为.
13. 将如图所示的“ ”笑脸放置在 的正方形网格中, 、 、 三点均在格点上.若 、 的坐标分别为 , ,则点 的坐标为.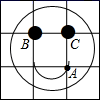 14. 如右图,一只蚂蚁沿着边长为2的正方体表面从点A出发,经过3个面爬到点B,如果它运动的路径是最短的,则此最短路径的长为.
14. 如右图,一只蚂蚁沿着边长为2的正方体表面从点A出发,经过3个面爬到点B,如果它运动的路径是最短的,则此最短路径的长为. 15. 如图,△ABC中,边AB的垂直平分线分别交BC、AB于点D、E,AE=3cm,△ABC的周长为17cm,则△ADC的周长是cm.
15. 如图,△ABC中,边AB的垂直平分线分别交BC、AB于点D、E,AE=3cm,△ABC的周长为17cm,则△ADC的周长是cm. 16. 如图所示, , , , , ,则 的度数是.
16. 如图所示, , , , , ,则 的度数是.
三、解答题
-
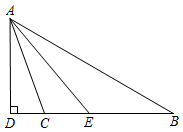
17. 解下列不等式(组),并把第(2)题的解集表示在数轴上.(1)、5x+3≤3(2+x);(2)、 .18. 如图,在△ABC中,∠B=30°,∠ACB=110°,AD是BC边上高线,AE平分∠BAC,求∠DAE的度数.
 19. 如图,一次函数y=﹣2x+3的图象交x轴于点A,交y轴于点B,点P在线段AB上(不与点A,B重合),过点P分别作OA和OB的垂线,垂足为C,D.当矩形OCPD的面积为1时,求此时P点的坐标.
19. 如图,一次函数y=﹣2x+3的图象交x轴于点A,交y轴于点B,点P在线段AB上(不与点A,B重合),过点P分别作OA和OB的垂线,垂足为C,D.当矩形OCPD的面积为1时,求此时P点的坐标. 20. 已知,如图,点A,D,B,E在同一条直线上, , 与 交于点G.
20. 已知,如图,点A,D,B,E在同一条直线上, , 与 交于点G. (1)、求证: ;(2)、当 时,求 的度数.21. 如图,A、B两点在射线OM、ON上,CF垂直平分AB,垂足为F, , ,垂足分别为D、E,且 .
(1)、求证: ;(2)、当 时,求 的度数.21. 如图,A、B两点在射线OM、ON上,CF垂直平分AB,垂足为F, , ,垂足分别为D、E,且 . (1)、求证:OC平分 ;(2)、如果 , ,求OD的长.22. 某校开学初在超市购进A、B两种品牌的消毒液,已知购买一瓶B品牌消毒液比购买一瓶A品牌消毒液多花30元.购买4瓶A品牌消毒液和5瓶B品牌消毒液需要花费600元.(1)、购买一瓶A品牌、一瓶B品牌消毒液各需多少元?(2)、该校为了防疫,决定再次购进A、B两种品牌的消毒液共50瓶,恰逢超市对这两种品牌消毒液的售价进行调整,A品牌消毒液售价比第一次购买时提高了8%,B品牌消毒液按第一次购买时售价的9折出售,如果该校此次购买的总费用不超过3260元,那么,最多可以购买多少瓶B品牌消毒液?23. 在平面直角坐标系中,点 的坐标是 .(1)、若点 在 轴上,求 的值及点 的坐标;(2)、若点 在第二象限且到 轴的距离与到 轴的距离相等,求 的值及点A的坐标.24. 在一条笔直的公路旁依次有 、 、 三个村庄,甲、乙两人同时分别从 、 两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向 村,最终到达 村.设甲、乙两人到 村的距离 , 与行驶时间 之间的函数关系如图所示,请回答下列问题:
(1)、求证:OC平分 ;(2)、如果 , ,求OD的长.22. 某校开学初在超市购进A、B两种品牌的消毒液,已知购买一瓶B品牌消毒液比购买一瓶A品牌消毒液多花30元.购买4瓶A品牌消毒液和5瓶B品牌消毒液需要花费600元.(1)、购买一瓶A品牌、一瓶B品牌消毒液各需多少元?(2)、该校为了防疫,决定再次购进A、B两种品牌的消毒液共50瓶,恰逢超市对这两种品牌消毒液的售价进行调整,A品牌消毒液售价比第一次购买时提高了8%,B品牌消毒液按第一次购买时售价的9折出售,如果该校此次购买的总费用不超过3260元,那么,最多可以购买多少瓶B品牌消毒液?23. 在平面直角坐标系中,点 的坐标是 .(1)、若点 在 轴上,求 的值及点 的坐标;(2)、若点 在第二象限且到 轴的距离与到 轴的距离相等,求 的值及点A的坐标.24. 在一条笔直的公路旁依次有 、 、 三个村庄,甲、乙两人同时分别从 、 两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向 村,最终到达 村.设甲、乙两人到 村的距离 , 与行驶时间 之间的函数关系如图所示,请回答下列问题: (1)、 、 两村间的距离为 , ;(2)、求出甲、乙两人到 村的距离 , 与行驶时间 之间的函数关系式,并求出图中点 的坐标;(3)、乙在行驶过程中,何时距甲 ?
(1)、 、 两村间的距离为 , ;(2)、求出甲、乙两人到 村的距离 , 与行驶时间 之间的函数关系式,并求出图中点 的坐标;(3)、乙在行驶过程中,何时距甲 ?