2022年苏科版初中数学《中考一轮复习》专题三 函数 3.3 反比例函数的图象与性质
试卷更新日期:2021-12-07 类型:一轮复习
一、单选题
-
1. 已知反比例函数y= ,则( )A、y随x的增大而增大 B、当x>-3且x≠0时,y>4 C、图象位于一、三象限 D、当y<-3时,0<x<42. 若双曲线y= 的图象的一支位于第三象限,则k的取值范围是( )A、k<1 B、k>1 C、0<k<1 D、无解3. 在反比例函数 ( 为常数)上有三点 , , ,若 ,则 , , 的大小关系为( )A、 B、 C、 D、4. 如图,正比例函数 的图象与反比例函数 的图象相交于A,B两点,点B的横坐标为2,当 时,x的取值范围是( )
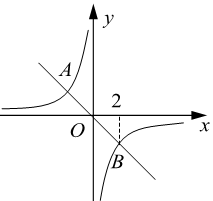 A、 或 B、 或 C、 或 D、 或5. 如图,点 和点 分别是反比例函数 和 的图像上的点, 轴,点 为 轴上一点,若 ,则 的值为( )
A、 或 B、 或 C、 或 D、 或5. 如图,点 和点 分别是反比例函数 和 的图像上的点, 轴,点 为 轴上一点,若 ,则 的值为( ) A、2 B、4 C、6 D、86. 如图,等边三角形OAB的一边OA在x轴上,双曲线y=在第一象限内的图象经过OB边的中点C,则点B的坐标是( )
A、2 B、4 C、6 D、86. 如图,等边三角形OAB的一边OA在x轴上,双曲线y=在第一象限内的图象经过OB边的中点C,则点B的坐标是( ) A、(1,) B、( , 1) C、(2,2) D、(2 , 2)7. 如图,在平面直角坐标系中,反比例函数 的图象交矩形OABC的边AB于点D交边BC于点E,且BE=2EC,若四边形ODBE的面积为8,则k的值为( )
A、(1,) B、( , 1) C、(2,2) D、(2 , 2)7. 如图,在平面直角坐标系中,反比例函数 的图象交矩形OABC的边AB于点D交边BC于点E,且BE=2EC,若四边形ODBE的面积为8,则k的值为( )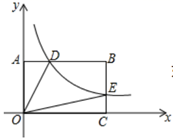 A、3 B、4 C、6 D、128. 如图,已知 , ( , ),反比例函数 的图象与线段 交于 , 两点,若 ,则 ( )
A、3 B、4 C、6 D、128. 如图,已知 , ( , ),反比例函数 的图象与线段 交于 , 两点,若 ,则 ( ) A、 B、4 C、3 D、9. 如图,平行四边形 的顶A在x轴的正半轴上,点 在对角线 上,反比例函数 的图像经过C、D两点.已知平行四边形 的面积是 ,则点B的坐标为( )
A、 B、4 C、3 D、9. 如图,平行四边形 的顶A在x轴的正半轴上,点 在对角线 上,反比例函数 的图像经过C、D两点.已知平行四边形 的面积是 ,则点B的坐标为( )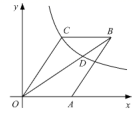 A、 B、 C、 D、10. 如图,在 轴正半轴上依次截取 ,过点 、 、 、…… 分别作 轴的垂线,与反比例函数 交于点 、 、 、…、 ,连接 、 、… ,过点 、 、…、 分别向 、 、…、 作垂线段,构成的一系列直角三角形(图中阴影部分)的面积和等于( ).
A、 B、 C、 D、10. 如图,在 轴正半轴上依次截取 ,过点 、 、 、…… 分别作 轴的垂线,与反比例函数 交于点 、 、 、…、 ,连接 、 、… ,过点 、 、…、 分别向 、 、…、 作垂线段,构成的一系列直角三角形(图中阴影部分)的面积和等于( ).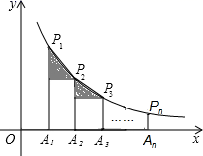 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 反比例函数的图象经过点 ,则这个反比例函数的解析式为 .12. 若点A(﹣1,y1)、B(1,y2)、C(3,y3)在反比例函数 的图象上,则y1、y2、y3的大小关系是.13. 已知点 在双曲线 上,点 在直线 上,则 的值为.14. 若直线 和双曲线 交于 两点,那么 .15. 如图,平面直角坐标系中,点A是x轴上任意一点, 轴,分别交 , 的图象于B、C两点,若 的面积为2,则k的值为 .
 16. 如图,点A在双曲线y= (x>0)上,点B在双曲线y= (x>0)上,且AB∥x轴,BC∥y轴,点C在x轴上,则△ABC的面积为 .
16. 如图,点A在双曲线y= (x>0)上,点B在双曲线y= (x>0)上,且AB∥x轴,BC∥y轴,点C在x轴上,则△ABC的面积为 . 17. 如图,点 在双曲线 上,点 在双曲线 上,点 在点 的左侧, 轴,点 , 在 轴上,若四边形 为面积是8的矩形,则 的值为 .
17. 如图,点 在双曲线 上,点 在双曲线 上,点 在点 的左侧, 轴,点 , 在 轴上,若四边形 为面积是8的矩形,则 的值为 . 18. 如图,菱形 顶点 在函数 的图象上,函数 的图象关于直线 对称,且经过点 , 两点,若 , ,则 的值为.
18. 如图,菱形 顶点 在函数 的图象上,函数 的图象关于直线 对称,且经过点 , 两点,若 , ,则 的值为.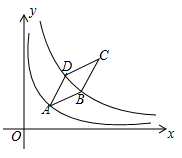
三、解答题
-
19. 已知函数 是反比例函数,求 的值.20. 已知反比例函数 的图象经过点 .(1)、试确定此反比例函数的解析式;(2)、设点 为图象上的一点,且 ,求 值.21. 如图,正比例函数y=kx(k>0)与反比例函数y= 的图象相交于A,C两点,过点A作x轴的垂线交x轴于点B,连接BC,则 的面积等于多少?
 22. 如图,一次函数 的图象与反比例函数 的图象交于A(2,4),B(8,n)两点.
22. 如图,一次函数 的图象与反比例函数 的图象交于A(2,4),B(8,n)两点. (1)、分别求出一次函数与反比例函数的解析式;(2)、求△OAB的面积.23. 如图,一次函数 的图象与反比例函数 的图象交于 , 两点.
(1)、分别求出一次函数与反比例函数的解析式;(2)、求△OAB的面积.23. 如图,一次函数 的图象与反比例函数 的图象交于 , 两点.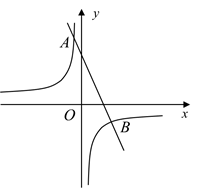 (1)、求一次函数和反比例函数的解析式;(2)、点 在 轴上,且满足 的面积等于4,请直接写出点 的坐标.24. 如图,已知反比例函数 的图象与一次函数 的图象在第一象限交于 两点
(1)、求一次函数和反比例函数的解析式;(2)、点 在 轴上,且满足 的面积等于4,请直接写出点 的坐标.24. 如图,已知反比例函数 的图象与一次函数 的图象在第一象限交于 两点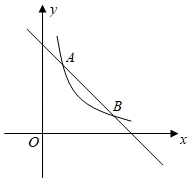 (1)、求反比例函数和一次函数的表达式;(2)、已知点 ,过点 作平行于 轴的直线,在第一象限内交一次函数 的图象于点 ,交反比例函数 上的图象于点 .若 ,结合函数图象直接写出 的取值范围.25. 如图,一次函数y= x+1的图象与轴交于点A , 与y轴交于点C , 与反比例函数y= (k≠0)的图象交于B , D两点,且AC=BC .
(1)、求反比例函数和一次函数的表达式;(2)、已知点 ,过点 作平行于 轴的直线,在第一象限内交一次函数 的图象于点 ,交反比例函数 上的图象于点 .若 ,结合函数图象直接写出 的取值范围.25. 如图,一次函数y= x+1的图象与轴交于点A , 与y轴交于点C , 与反比例函数y= (k≠0)的图象交于B , D两点,且AC=BC . (1)、写出点A , B的坐标;(2)、求出点D的坐标,并直接写出当 > x+1时,x的取值范围;(3)、若P是x轴上一点,PM⊥x轴交一次函数于点M , 交反比例函数于点N , 当O , C , M , N为顶点的四边形为平行四边形时,请直接写出点P的坐标.26. 如图,在直角坐标系xOy中,直线y=2x+6 与反比例函数 的图象交于点A(1,m),与x轴交于点B ,与y 轴交于点D .
(1)、写出点A , B的坐标;(2)、求出点D的坐标,并直接写出当 > x+1时,x的取值范围;(3)、若P是x轴上一点,PM⊥x轴交一次函数于点M , 交反比例函数于点N , 当O , C , M , N为顶点的四边形为平行四边形时,请直接写出点P的坐标.26. 如图,在直角坐标系xOy中,直线y=2x+6 与反比例函数 的图象交于点A(1,m),与x轴交于点B ,与y 轴交于点D . (1)、求m的值和反比例函数的表达式;(2)、在y轴上有一动点P(0,n),过点P作平行于x轴的直线,交反比例函数的图象于点M,交直线AB于点N,且点M在点A下方,连接BM.若 ,求n的值.27. 如图,在平面直角坐标系中,A (6,0)、B(0, 4)是矩形OACB的两个顶点,双曲线 (k≠0,x>0)经过AC的中点D,点E是矩形OACB与双曲线 的另一个交点,
(1)、求m的值和反比例函数的表达式;(2)、在y轴上有一动点P(0,n),过点P作平行于x轴的直线,交反比例函数的图象于点M,交直线AB于点N,且点M在点A下方,连接BM.若 ,求n的值.27. 如图,在平面直角坐标系中,A (6,0)、B(0, 4)是矩形OACB的两个顶点,双曲线 (k≠0,x>0)经过AC的中点D,点E是矩形OACB与双曲线 的另一个交点,
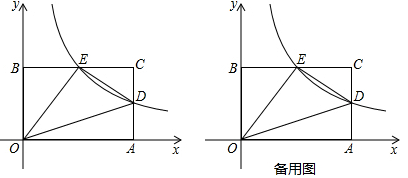 (1)、点D的坐标为 , 点E的坐标为.(2)、动点P在第一象限内,且满足 .
(1)、点D的坐标为 , 点E的坐标为.(2)、动点P在第一象限内,且满足 .①若点P在这个反比例函数的图象上,求点P的坐标;
②连接PO、PE,当PO-PE的值最大时,求点P的坐标;
③若点Q是平面内一点,使得以A、C、P、Q为顶点的四边形是菱形,请你直接写出满足条件的所有点Q的坐标.
28. 已知一次函数 和反比例函数 .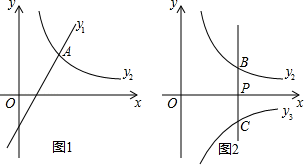 (1)、如图1,若 ,且函数 、 的图象都经过点 .
(1)、如图1,若 ,且函数 、 的图象都经过点 .①求 , 的值;
②直接写出当 时 的范围;
(2)、如图2,过点 作 轴的平行线 与函数 的图象相交于点 ,与反比例函数 的图象相交于点 .①若 ,直线 与函数 的图象相交点 .当点 、 、 中的一点到另外两点的距离相等时,求 的值;
②过点 作 轴的平行线与函数 的图象相交于点 .当 的值取不大于1的任意实数时,点 、 间的距离与点 、 间的距离之和 始终是一个定值.求此时 的值及定值 .