河南省南阳市2021-2022学年高二上学期数学期中考试试卷

试卷更新日期：2021-12-07 类型：期中考试

进入出卷网下载

一、单选题

1. 已知非零实数 $a$ ， $b$ ，若 $a > b$ ，则下列不等式成立的是（）

A、 $\frac{1}{a} > \frac{1}{b}$ B、 $a^{2} > b^{2}$ C、 $\frac{1}{a} < \frac{1}{b}$ D、 $a^{3} > b^{3}$

查看试题解析
2. 在数列{ ${a_{n}}$ 中， $a_{1} = 1$ ， $a_{n + 1} - a_{n} = 2$ ， $n \in N_{+}$ ，则 $a_{10}$ 的值为（）

A、17 B、18 C、19 D、21

查看试题解析
3. 《算法统宗》是中国古代数学名著，许多数学问题都是以歌诀形式呈现的.“九儿问甲歌”就是其中一首：一个公公九个儿，若问生年总不知，自长排来差三岁，共年二百又零七，借问小儿多少岁，各儿岁数要详推.这位公公年龄最小的儿子年龄为（）

A、8岁 B、9岁 C、11岁 D、12岁

查看试题解析
4. 在下列函数中，最小值是2的为（）

A、 $y = x + \frac{1}{x}$ B、 $y = 3^{x} + 3^{- x}$ C、 $y = \ln x + \frac{1}{\ln x} (1 < x < e)$ D、 $y = \sin x + \frac{1}{\sin x} (0 < x < \frac{π}{2})$

查看试题解析
5. 设变量 $x ， y$ 满足约束条件 ${\begin{matrix} x + y - 2 \geq 0 \\ x - 2 y + 4 \geq 0 \\ 2 x - y - 4 \geq 0 \end{matrix}$ ，则 $z = 2 x + y$ 的最小值为（）

A、2 B、4 C、-2 D、12

查看试题解析
6. 在 $△ A B C$ 中， $\sin A ： \sin B ： \sin C = 7 ： 5 ： 3$ ，则该三角形的最大内角是（）

A、135° B、120° C、84° D、75°

查看试题解析
7. 已知等差数列 ${a_{n}}$ 满足 $S_{9} = 27$ ， $S_{n} = 330$ ， $a_{n - 4} = 30$ ，则 $n$ 值为（）

A、20 B、19 C、18 D、17

查看试题解析
8. 已知 $△ A B C$ 的内角 $A$ ， $B$ ， $C$ 的对边分别为 $a$ ， $b$ ， $c$ ，若 $a = 2$ ， $b = 1$ ， $C = 2 B$ ，则 $△ A B C$ 外接圆半径为（）

A、2 B、 $\sqrt{3}$ C、 $\sqrt{2}$ D、1

查看试题解析
9. 已知数列 ${a_{n}}$ 是等差数列，若 $a_{9} + 3 a_{11} < 0$ ， $a_{10} \cdot a_{11} < 0$ ，且数列 ${a_{n}}$ 的前 $n$ 项和 $S_{n}$ 有最大值，那么 $S_{n}$ 取得最小正值时 $n$ 等于（）

A、19 B、20 C、21 D、22

查看试题解析
10. 在 $△ A B C$ 中， $a$ ， $b$ ， $c$ 分别是角 $A$ ， $B$ ， $C$ 对边的长，根据下列条件解三角形，有两解的是（）

A、 $a = 7$ ， $b = 14$ ， $A = 30 °$ B、 $a = 30$ ， $b = 25$ ， $A = 150 °$ C、 $a = 72$ ， $b = 50$ ， $A = 135 °$ D、 $a = 30$ ， $b = 40$ ， $A = 26 °$

查看试题解析
11. 在数列 ${a_{n}}$ 中， $a_{1} = 1$ ， $a_{2} = 3$ ， $a_{3} = 5$ ， $a_{n} a_{n + 3} = 1$ ，则 $\log_{5} a_{1} + \log_{5} a_{2} + \cdot \cdot \cdot + \log_{5} a_{2021} =$ （）

A、0 B、1 C、 $\log_{5} 3$ D、 $\log_{5} 15$

查看试题解析
12. 已知数列 ${a_{n}}$ 满足 $a_{1} = 1$ ， $a_{2 n} = a_{2 n - 1} + {(- 1)}^{n}$ ， $a_{2 n + 1} = a_{2 n} + 3^{n} (n \in N^{*})$ ，则数列 ${a_{n}}$ 的前2021项的和为（）

A、 $3^{1011} - 2022$ B、 $3^{1010} - 2022$ C、 $3^{1011} - 2020$ D、 $3^{1010} - 2020$

查看试题解析

二、填空题

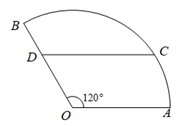
13. 已知关于 $x$ 的不等式 $x^{2} + b x + c > 0$ 的解集是{ $x | x < - 2$ 或 $x > - \frac{1}{2}$ }，则 $x^{2} - b x + c < 0$ 的解集为.

查看试题解析
14. $△ A B C$ 中， $\cos B = \frac{5}{13}$ ， $\sin A = \frac{3}{5}$ ，则在 $△ A B C$ 中， $\cos C =$ .

查看试题解析
15. 如图是某商业小区的平面设计图，初步设计该小区为半径是200米，圆心角是120°的扇形 $A O B$ . $O$ 为南门位置， $C$ 为东门位置，小区里有一条平行于 $A O$ 的小路 $C D$ ，若 $O D = \frac{200 \sqrt{6}}{3}$ 米，则圆弧 $A C$ 的长为米

查看试题解析
16. 正数 $a$ ， $b$ 满足 $\frac{1}{a} + \frac{9}{b} = 1$ ，若不等式 $a + b \geq - x^{2} + 4 x + 18 - m$ 对 $\forall x \in [- 3 ， - 1]$ 恒成立，则实数 $m$ 的取值范围是.

查看试题解析

三、解答题

17. 在△ABC中，角A，B，C所对的边分别为a，b，c，设S为△ABC的面积，满足 $S = \frac{\sqrt{3}}{4} (a^{2} + b^{2} - c^{2})$ ．
（Ⅰ）求角C的大小；

（Ⅱ）求 $\sin A + \sin B$ 的最大值．

查看试题解析
18. 设函数 $f (x) = a x^{2} - (a + 1) x + 1$ .当 $a \in R$ 时，求关于 $x$ 的不等式 $f (x) < 0$ 的解集.

查看试题解析
19. 若数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，且 $S_{n} = 2 a_{n} - 1$ ；数列 ${b_{n}}$ 满足 $b_{n - 1} - b_{n} = b_{n} b_{n - 1} (n \geq 2 ， n \in N)$ ， $b_{1} = 1$ .

(1)、求数列 ${a_{n}}$ ， ${b_{n}}$ 的通项公式；

(2)、求数列 ${\frac{a_{n}}{b_{n}}}$ 的前 $n$ 项和 $T_{n}$ .

查看试题解析
20. 设 $△ A B C$ 的内角A，B，C的对边分别为a，b，c ，且 $a \sin A - c \sin C = b (\sin A - \sin B)$ .

(1)、求角C；

(2)、若 $c = 1$ ，且 $△ A B C$ 的面积 $S \in (0 ， \frac{\sqrt{3}}{12})$ ，求 $△ A B C$ 的周长l的取值范围.

查看试题解析
21. 首届世界低碳经济大会在南昌召开，本届大会以“节能减排，绿色生态”为主题.某单位在国家科研部门的支持下，进行技术攻关，采用了新工艺，把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨，最多为600吨，月处理成本 $y$ （元）与月处理量 $x$ （吨）之间的函数关系可近似地表示为 $y = \frac{x^{2}}{2} - 200 x + 80000$ ，且每处理一吨二氧化碳得到可利用的化工产品价值为100元.

(1)、该单位每月处理量为多少吨时，才能使每吨的平均处理成本最低?

(2)、该单位每月能否获利?如果获利，求出最大利润；如果不获利，则需要国家至少补贴多少元才能使该单位不亏损?

查看试题解析
22. 设数列 ${a_{n}}$ 满足 $a_{1} = 3$ ， $a_{n + 1} = 2 a_{n} - n + 1$ .

(1)、证明数列 ${a_{n} - n}$ 为等比数列，并求数列 ${a_{n}}$ 的通项公式；

(2)、若 $c_{1} = 1$ ， $b_{n} = c_{n + 1} - c_{n} = \frac{1}{a_{n} - n}$ ， $d_{n} = \frac{1}{c_{n}} - \frac{1}{c_{n + 1}}$ .求证：数列 ${b_{n} \cdot d_{n}}$ 的前 $n$ 项和 $S_{n} < \frac{1}{4}$ .

查看试题解析