河南省开封市五县2021-2022学年高二上学期理数期中联考试卷

试卷更新日期：2021-12-07 类型：期中考试

进入出卷网下载

一、单选题

1. 椭圆 $\frac{x^{2}}{4} + \frac{y^{2}}{a^{2}} = 1$ 与双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{2} = 1$ 有相同的焦点，则实数a等于（）

A、 $\frac{1}{2}$ B、-1 C、1 D、-1或1

查看试题解析
2. 祖暅原理：“幂势既同，则积不容异”.意思是说：两个同高的几何体，如在等高处的截面积恒相等，则体积相等.设 $A$ 、 $B$ 为两个同高的几何体， $p :$ $A$ 、 $B$ 的体积不相等， $q :$ $A$ 、 $B$ 在等高处的截面积不恒相等.根据祖暅原理可知， $p$ 是 $q$ 的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
3. 已知 $x > 0$ ， $y > 0$ ， $x$ ， $a$ ， $b$ ， $y$ 成等差数列， $x$ ， $c$ ， $d$ ， $y$ 成等比数列，则 $\frac{c d}{{(a + b)}^{2}}$ 的最大值是（）

A、0 B、1 C、2 D、 $\frac{1}{4}$

查看试题解析
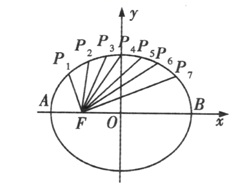4. 如图，把椭圆 $\frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$ 的长轴 $A B$ 分成8等份，过每个分点作 $x$ 轴的垂线分别交椭圆的上半部分于点 $P_{1}$ ， $P_{2}$ ，…， $P_{7}$ ， $F$ 是左焦点，则 $| P_{1} F | + | P_{2} F | + \cdot \cdot \cdot + | P_{7} F | =$ （）

A、21 B、28 C、35 D、42

查看试题解析
5. 在抚顺二中运动会开幕式中，某班级的“蝴蝶振翅”节目获得一致称赞，其形状近似于双曲线，在“振翅”过程中，双曲线的渐近线与对称轴的夹角 $α$ 为某一范围内变动， $\frac{π}{6} \leq α \leq \frac{π}{3}$ ，则该双曲线的离心率取值范围是（）

A、 $[\frac{4}{3} ， 4]$ B、 $[\frac{2 \sqrt{3}}{3} ， 4]$ C、 $[\frac{2 \sqrt{3}}{3} ， 2]$ D、 $[\frac{4}{3} ， 2]$

查看试题解析
6. 在 $△ A B C$ 中，角 $A$ ， $B$ ， $C$ 所对的边分别为 $a$ ， $b$ ， $c$ ，满足 $a \cos A = b \cos B$ ，则 $△ A B C$ 的形状为（）

A、等腰三角形 B、直角三角形 C、等腰直角三角形 D、等腰或直角三角形

查看试题解析
7. 已知 $x > 0 ， y > - 1$ ，且 $\frac{4}{x} + \frac{1}{y + 1} = 3$ ，则 $x + y$ 的最小值为（）

A、4 B、3 C、2 D、1

查看试题解析
8. “ $a = \frac{1}{2}$ ”是“直线 $l_{1}$ ： $2 a x + 4 y + 3 = 0$ 与直线 $l_{2}$ ： $x - {(a - 1)}^{2} y - 5 = 0$ 垂直”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
9. 北京天坛的圜丘坛为古代祭天的场所，分上、中、下三层，上层中心有一块圆形石板(称为天心石)，环绕天心石砌9块扇面形石板构成第一环，向外每环依次增加9块，下一层的第一环比上一层的最后一环多9块，向外每环依次也增加9块，已知每层环数相同，且下层比中层多729块，则三层共有扇面形石板(不含天心石)（）

A、3699块 B、3474块 C、3402块 D、3339块

查看试题解析
10. 下列五个命题：
①命题“若 $a = 0$ ，则 $a b = 0$ ”的否命题是“若 $a = 0$ ，则 $a b \neq 0$ ”；②若命题 $p$ ： $\exists x \in R$ ， $x^{2} + x + 1 < 0$ ，则 $\neg p$ ： $\forall x \in R$ ， $x^{2} + x + 1 \geq 0$ ；③若命题“ $\neg p$ ”与命题“ $p$ 或 $q$ ”都是真命题，则命题 $q$ 一定是真命题；④命题“若 $0 < a < 1$ ，则 $\log_{a} (a + 1) < \log_{a} (1 + \frac{1}{a})$ ”是真命题；⑤命题“集合 ${x | x^{2} - 2 x + 1 = 0 ， x \in R}$ 有2个子集”是假命题．其中正确命题的序号是（）

A、②③ B、①② C、④⑤ D、③④

查看试题解析
11. 太极图被称为“中华第一图”．从孔庙大成殿梁柱，到楼观台、三茅宫标记物；从道袍、挂摊、中医、气功、武术到韩国国旗……，太极图无不跃居其上．这种广为人知的太极图，其形状如阴阳两鱼互抱在一起，因而被称为“阴阳鱼太极图”．在某个太极图图案中，阴影部分可表示为 $A = {(x ， y) | x^{2} + {(y - 1)}^{2} \leq 1 或 {\begin{array}{l} x^{2} + y^{2} \leq 4 \\ x^{2} + {(y + 1)}^{2} \geq 1 \\ x \leq 0 \end{array}}$ ，设点 $(x ， y) \in A$ ，则 $z = 3 x + 4 y$ 的最大值与最小值之和为（）

A、-1 B、19 C、1 D、20

查看试题解析
12. 已知点 $A$ 是椭圆 $\frac{x^{2}}{2} + y^{2} = 1$ 的上顶点， $F_{1} ， F_{2}$ 分别是椭圆左右焦点，直线 $y = a x + b (a > 0)$ 将三角形 $A F_{1} F_{2}$ 分割为面积相等两部分，则 $b$ 的取值范围是（）

A、 $(0 ， 1)$ B、 $(1 - \frac{\sqrt{2}}{2} ， \frac{1}{2})$ C、 $(1 - \frac{\sqrt{2}}{2} ， \frac{1}{3}]$ D、 $[\frac{1}{3} ， \frac{1}{2})$

查看试题解析

二、填空题

13. 古希腊数学家阿波罗尼奥斯的著作《圆锥曲线论》中给出了圆的另一种定义：平面内，到两个定点 $A ， B$ 距离之比是常数 $λ (λ > 0 ， λ \neq 1)$ 的点 $M$ 的轨迹是圆，若两定点 $A ， B$ 的距离为3，动点 $M$ 满足 $| M A | = 2 | M B |$ ，则 $M$ 点的轨迹围成区域的面积为.

查看试题解析
14. 记不等式组 ${\begin{array}{l} x + y ⩾ 6 \\ 2 x - y \geq 0 \end{array}$ 表示的平面区域为 $D$ ，命题 $p ： \exists (x ， y) \in D ， 2 x + y ⩾ 9$ ；命题 $q ： \forall (x ， y) \in D ， 2 x + y ⩽ 12$ .给出了四个命题：① $p \lor q$ ；② $\neg p \lor q$ ；③ $p \land \neg q$ ；④ $\neg p \land \neg q$ ，这四个命题中，所有真命题的编号是

查看试题解析
15. 在 $△ A B C$ 中， $A ， B ， C$ 分别为 $a ， b ， c$ 边所对的角，若 $a ， b ， c$ 成等差数列，则 $B$ 的取值范围是．

查看试题解析
16. 函数 $y = \sqrt{x^{2} + 4} + \sqrt{x^{2} + 6 x + 18}$ 的最小值为．

查看试题解析

三、解答题

17. 已知命题 $p ： \exists x_{0} \in {x | - 1 \leq x \leq 1}$ ， $x_{0}^{2} - x_{0} - m \geq 0$ 是假命题.

(1)、求实数 $m$ 的取值集合 $B$ ；

(2)、设不等式 $(x - 3 a) (x - a - 2) < 0$ 的解集为 $A$ .若 $x \in B$ 是 $x \in A$ 的必要不充分条件，求实数 $a$ 的取值范围.

查看试题解析
18. 在△ABC中，a， b， c分别为内角A， B， C的对边，且 $2 a \sin A = (2 b + c) \sin B + (2 c + b) \sin C .$
（Ⅰ）求A的大小；

（Ⅱ）求 $\sin B + \sin C$ 的最大值.

查看试题解析
19. 设 ${a_{n}}$ 是首项为1的等比数列，数列 ${b_{n}}$ 满足 $b_{n} = \frac{n a_{n}}{3}$ ，已知 $a_{1}$ ，3 $a_{2}$ ，9 $a_{3}$ 成等差数列.

(1)、求 ${a_{n}}$ 和 ${b_{n}}$ 的通项公式；

(2)、记 $S_{n}$ 和 $T_{n}$ 分别为 ${a_{n}}$ 和 ${b_{n}}$ 的前n项和.证明： $T_{n}$ < $\frac{S_{n}}{2}$ .

查看试题解析
20. 等比数列 ${a_{n}}$ 的各项均为正数，且 $2 a_{1} + 3 a_{2} = 1, a_{3}^{2} = 9 a_{2} a_{6}$ .

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、设b_n＝log₃a₁＋log₃a₂＋…＋log₃a_n ，求数列 ${\frac{1}{b_{n}}}$ 的前 $n$ 项和 $T_{n}$ .

查看试题解析
21. 已知圆 $C_{1} ： x^{2} + y^{2} - 2 m x - 4 m y + 5 m^{2} - 4 = 0$ ，圆 $C_{2} ： x^{2} + y^{2} = 1$

(1)、若圆 $C_{1}$ 、 $C_{2}$ 相交，求 $m$ 的取值范围；

(2)、若圆 $C_{1}$ 与直线 $l ： x + 2 y - 4 = 0$ 相交于 $M$ 、 $N$ 两点，且 $| M N | = \frac{4 \sqrt{5}}{5}$ ，求 $m$ 的值；

(3)、已知点 $P (2 ， 0)$ ，圆 $C_{1}$ 上一点 $A$ ，圆 $C_{2}$ 上一点 $B$ ，求 $| \vec{P A} + \vec{P B} |$ 的最小值的取值范围．

查看试题解析
22. 已知斜率为 $k$ 的直线 $l$ 与椭圆 $C$ ： $\frac{x^{2}}{4} + \frac{y^{2}}{3} = 1$ 交于 $A$ ， $B$ 两点．

(1)、若线段 $A B$ 的中点为 $M (1 ， \frac{3}{4})$ ，求 $k$ 的值；

(2)、若 $O A ⊥ O B$ ，求证：原点 $O$ 到直线 $l$ 的距离为定值．

查看试题解析