浙江省金华市丽泽书院2021-2022学年八年级上学期数学期中独立作业试题卷
试卷更新日期:2021-12-07 类型:期中考试
一、选择题(每小题3分,共10小题).
-
1. 要使 有意义,则实数x的取值范围是( )A、x≥1 B、x≥0 C、x≥﹣1 D、x≤02. 已知三角形的两边长分别为 和 ,第三边长为整数,则该三角形的周长为( )A、 B、 C、 D、3. 在平面直角坐标系中,将点P(1,4)向左平移3个单位长度得到点Q,则点Q所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 若x>y,则下列式子错误的是( )A、x﹣2>y﹣2 B、 C、﹣x<﹣y D、1﹣x>1﹣y5. 如图是作△ABC的作图痕迹,则此作图的已知条件是( )
 A、已知两边及夹角 B、已知三边 C、已知两角及夹边 D、已知两边及一边对角6. △ABC三边长为a、b、c,则下列条件能判断△ABC是直角三角形的是( )A、a=7,b=8,c=10 B、a= ,b=4,c=5 C、a= ,b=2,c= D、a=3,b=4,c=67. 若直线y=kx+b经过一、二、四象限,则直线y=bx﹣k的图象只能是图中的( )A、
A、已知两边及夹角 B、已知三边 C、已知两角及夹边 D、已知两边及一边对角6. △ABC三边长为a、b、c,则下列条件能判断△ABC是直角三角形的是( )A、a=7,b=8,c=10 B、a= ,b=4,c=5 C、a= ,b=2,c= D、a=3,b=4,c=67. 若直线y=kx+b经过一、二、四象限,则直线y=bx﹣k的图象只能是图中的( )A、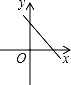 B、
B、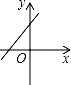 C、
C、 D、
D、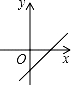 8. “三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动、C点固定,OC=CD=DE,点D、E可在槽中滑动.若∠BDE=75°,则∠CDE的度数是( )
8. “三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动、C点固定,OC=CD=DE,点D、E可在槽中滑动.若∠BDE=75°,则∠CDE的度数是( )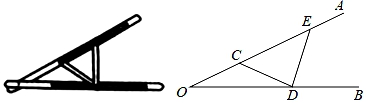 A、60° B、65° C、75° D、80°9. 关于x的不等式 有解,则a的取值范围是( )A、a<3 B、a≤3 C、a≥3 D、a>310. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点D在AB边上,AD=AC,AE⊥CD,垂足为F,与BC交于点E,则BE的长是( )
A、60° B、65° C、75° D、80°9. 关于x的不等式 有解,则a的取值范围是( )A、a<3 B、a≤3 C、a≥3 D、a>310. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点D在AB边上,AD=AC,AE⊥CD,垂足为F,与BC交于点E,则BE的长是( )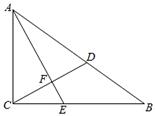 A、1.5 B、2.5 C、 D、3
A、1.5 B、2.5 C、 D、3二、填空题(每小题4分,共6小题)
-
11. 计算3 ﹣ 的结果是 .12. 如图,AD,BE是等边△ABC的两条高线,AD,BE交于点O,则∠AOB=度.
 13. 命题“若a2>b2则a>b”是命题(填“真”或“假”),它的逆命题是 .14. 如图,直线y=x+2与直线y=ax+c相交于点P(m,3).则关于x的不等式x+2≥ax+c的不等式的解为 .
13. 命题“若a2>b2则a>b”是命题(填“真”或“假”),它的逆命题是 .14. 如图,直线y=x+2与直线y=ax+c相交于点P(m,3).则关于x的不等式x+2≥ax+c的不等式的解为 .
 15. 如图,长方形ABCD中,AD=8,AB=4,BQ=5,点P在AD边上运动,当△BPQ为等腰三角形时,AP的长为 .
15. 如图,长方形ABCD中,AD=8,AB=4,BQ=5,点P在AD边上运动,当△BPQ为等腰三角形时,AP的长为 .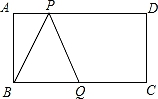 16. 如图,点E在△DBC边DB上,点A在△DBC内部,∠DAE=∠BAC=90°,AD=AE,AB=AC,给出下列结论,其中正确的是(填序号)
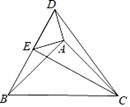
16. 如图,点E在△DBC边DB上,点A在△DBC内部,∠DAE=∠BAC=90°,AD=AE,AB=AC,给出下列结论,其中正确的是(填序号)①BD=CE;②∠DCB=∠ABD=45°;③BD⊥CE;④BE2=2(AD2+AB2).
三、解答题(共7小题)
-
17.(1)、化简: ﹣( ﹣ )(2)、解不等式组:18. 在平面直角坐标系中,点P(2﹣m,3m+6).(1)、若点P与x轴的距离为9,求m的值;(2)、若点P在过点A(2,﹣3)且与y轴平行的直线上,求点P的坐标.19. 某业主贷款88000元购进一台机器,生产某种产品,已知产品的成本是每个5元,售价是每个8元,应付的税款和其他费用是售价的10%,若每个月能生产、销售8000个产品,问至少几个月后能赚回这台机器贷款?(用列不等式的方法解决)20. 如图,∠ADB=∠ADC,∠B=∠C.
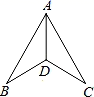 (1)、求证:AB=AC;(2)、连接BC,求证:AD⊥BC.21. 已知一次函数y1=kx+b(其中k、b为常数且k≠0)(1)、若一次函数y2=bx﹣k,y1与y2的图象交于点(2,3),求k,b的值;(2)、若b=k﹣1,当﹣2≤x≤2时,函数有最大值3,求此时一次函数y1的表达式.22. 如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D,E分别在AC,BC上,且CD=CE.
(1)、求证:AB=AC;(2)、连接BC,求证:AD⊥BC.21. 已知一次函数y1=kx+b(其中k、b为常数且k≠0)(1)、若一次函数y2=bx﹣k,y1与y2的图象交于点(2,3),求k,b的值;(2)、若b=k﹣1,当﹣2≤x≤2时,函数有最大值3,求此时一次函数y1的表达式.22. 如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D,E分别在AC,BC上,且CD=CE.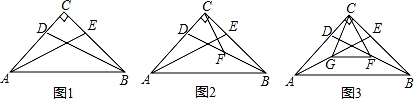 (1)、如图1,求证:∠CAE=∠CBD;(2)、如图2,F是BD的中点,求证:AE⊥CF;(3)、如图3,F,G分别是BD,AE的中点,若AC=2 ,CE=1,求△CGF的面积.23. 甲、乙两人相约周末沿同一条路线登山,甲、乙两人距地面的高度y(米)与登山时间x(分钟)之间的函数图象如图所示,根据图象所提供的信息解答下列问题
(1)、如图1,求证:∠CAE=∠CBD;(2)、如图2,F是BD的中点,求证:AE⊥CF;(3)、如图3,F,G分别是BD,AE的中点,若AC=2 ,CE=1,求△CGF的面积.23. 甲、乙两人相约周末沿同一条路线登山,甲、乙两人距地面的高度y(米)与登山时间x(分钟)之间的函数图象如图所示,根据图象所提供的信息解答下列问题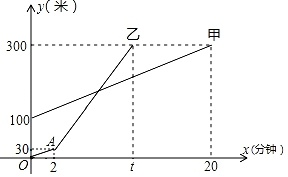 (1)、甲登山的速度是每分钟米;乙在A地提速时,甲距地面的高度为米;(2)、若乙提速后,乙的速度是甲登山速度的3倍;
(1)、甲登山的速度是每分钟米;乙在A地提速时,甲距地面的高度为米;(2)、若乙提速后,乙的速度是甲登山速度的3倍;①求乙登山全过程中,登山时距地面的高度y(米)与登山时间x(分钟)之间的函数解析式;
②乙计划在他提速后5分钟内追上甲,请判断乙的计划能实现吗?并说明理由;
(3)、当x为多少时,甲、乙两人距地面的高度差为80米?