浙江省宁波市鄞州区2021-2022学年九年级上学期期中考试数学试卷

试卷更新日期：2021-12-07 类型：期中考试

进入出卷网下载

一、选择题（每小题4分，共40分）

1. 抛物线 $y = 2 {(x - 3)}^{2} + 1$ 的顶点坐标是（）

A、(3，1) B、(3，-1) C、(－3，-1) D、(－3，1)

查看试题解析
2. 一条水管的截面如图所示，已知排水管的半径OB=10，水面宽AB=16，则截面圆心O到水面的距离OC的的长是（）

A、4 B、5 C、6 D、8

查看试题解析
3. 任意掷一枚骰子，下列情况出现的可能性比较大的是（）

A、面朝上的点数是3 B、面朝上的点数是奇数 C、面朝上的点数小于2 D、面朝上的点数不小于3

查看试题解析
4.
已知二次函数y=ax²+bx+c(a≠0)的图象如图所示，现有下列结论：① b²－4ac＞0 ② a＞0 ③ b＞0 ④ c＞0 ⑤9a+3b+c＜0，则其中结论正确的个数是（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
5. 如图，在Rt△ACB中，∠ACB=90°，∠A=35°，将△ABC绕点C逆时针旋转α角到△A₁B₁C的位置，A₁B₁恰好经过点B，则旋转角α的度数等（）

A、35° B、55° C、65° D、70°

查看试题解析
6. 从下列直角三角板与圆弧的位置关系中，可判断圆弧为半圆的是（）

A、 B、 C、 D、

查看试题解析
7. 如图所示，在正方形ABCD中，E是BC的中点，△DEF的面积等于2，则正方形ABCD的面积等于（）

A、6 B、12 C、16 D、20

查看试题解析
8. 如图，扇形AOB的圆心角为90°，四边形OCDE是边长为1的正方形，点C，E，D分别在OA，OB， $\overset{⌢}{A E}$ 上，过A作AF⊥ED交ED的延长线于点F，那么图中阴影部分的面积为（）

A、 $\frac{\sqrt{2}}{2}$ B、 $\sqrt{2} - 1$ C、 $2 - \sqrt{2}$ D、 $\sqrt{2}$

查看试题解析
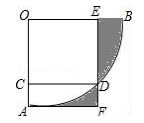9. 如图，C是以AB为直径的半圆O上一点，连结AC，BC，分别以AC，BC为斜边向外作等腰直角三角形△ACD，△BCE，弧AC和弧BC的中点分别是M，N．连接DM，EN，若C在半圆上由点A向B移动的过程中，DM∶EN的值的变化情况是（）

A、变大 B、变小 C、先变大再变小 D、保持不变

查看试题解析
10. 二维码已经给我们的生活带来了很大方便，它是由大小相同的黑白两色的小正方形（如图1中C）按某种规律组成的一个大正方形，现有25×25格式的正方形如图1，角上是三个7×7的A型大黑白相间正方形，中间右下一个5×5的B型黑白相间正方形，除这4个正方形外，若其他的小正方形白色块数y与黑色块数x正好满足如图2所示的函数图象，则该25×25格式的二维码共有多少块黑色的C型小正方形（）

A、153 B、218 C、100 D、216

查看试题解析

二、填空题（共6题，共30分）

11. 将抛物线y=4x²先向右平移一个单位，再向上平移3个单位，得到的抛物线是.

查看试题解析
12. 某中学七年级(2)班的“精英小组”有男生4人，女生3人，若选一人担任组长，则组长是男生的概率为.

查看试题解析
13. 已知正n边形的每一个内角都等于144°，则n的值为.

查看试题解析
14. 如图，在矩形ABCD中，AB=5，AD=2，点P是CD边上的一个动点，则当△ADP与△BCP相似时，DP=.

查看试题解析
15. 如图，点A是抛物线y=x²﹣4x对称轴上的一点，连接OA，以A为旋转中心将AO逆时针旋转90°得到AO′，当O′恰好落在抛物线上时，点A的坐标为.

查看试题解析
16. 如图，△ABC中，AB=4，∠ACB=75°，∠ABC=45°，D是线段BC上的一个动点，以AD为直径画⊙O分别交AB，AC于E，F，连接EF，则EF的最小值为。

查看试题解析

三、解答题（共8个小题，满分80分）

17. 已知a：b=3：2，求

(1)、 $\frac{a + b}{b}$

(2)、 $\frac{2 a - 7 b}{4 b}$ 的值；

查看试题解析
18. 如图，方格纸中的每个小正方形的边长都是1，△ABC是格点三角形（顶点在方格顶点处）．

(1)、求△ABC的面积；

(2)、在右边的格点图中画出一个格点△A₁B₁C₁ ，使得△A₁B₁C₁与△ABC相似，面积比为2：1．

查看试题解析
19. 现有4张正面分别写有数字1、2、3、4的卡片，将4张卡片的背面朝上，洗匀。

(1)、若从中任意抽取1张，抽的卡片上的数字恰好为3的概率是；

(2)、若先从中任意抽取1张（不放回），再从余下的3张中任意抽取1张，求抽得的2张卡片上的数字之和为3的倍数的概率。（请用“画树状图”或“列表”等方法写出分析过程）

查看试题解析
20. 小明同学在用描点法画二次函数y₁＝ax²+bx+c的图象时，由于粗心，他算错了一个y值，列出了下面表格：

x

…

-1

0

1

2

3

…

y＝ax²+bx+c

…

12

5

2

5

14

…

(1)、请求出这个二次函数解析式；

(2)、请指出这个错误的y值，并说明理由；

(3)、若直线 $y_{2} = m x + n$ 经过点（0，5）和（3，14）两点，则当 $y_{1} < y_{2}$ 时，请直接写出x的取值范围.

查看试题解析
21. 如图，在△ABC中，AB＝AC．以BC为直径画圆O分别交AB，AC与点D，E.

(1)、求证：BD＝CE；

(2)、当△ABC中 $∠ B = 70 °$ 且BC＝12时，求 $\overset{⌢}{D E}$ 的长．

查看试题解析
22. 某游乐场的圆形喷水池中心O有一雕塑OA，从A点向四周喷水，喷出的水柱为抛物线，且形状相同．如图，以水平方向为x轴，点O为原点建立直角坐标系，点A在y轴上，x轴上的点C，D为水柱的落水点，水柱所在抛物线（第一象限部分）的函数表达式为 $y = - \frac{1}{6} {(x - 5)}^{2} + 6$ ．

(1)、求雕塑高OA．

(2)、求落水点C，D之间的距离．

(3)、若需要在OD上的点E处竖立雕塑EF，OE＝10m，EF＝1.8m，EF⊥OD．问：顶部F是否会碰到水柱？请通过计算说明．

查看试题解析
23.

(1)、【基础巩固】如图1，点A，F，B在同一直线上，若∠A=∠B=∠EFC，求证：△AFE∽△BCF；

(2)、【尝试应用】如图2，AB是半圆⊙O的直径，弦长AC=BC=4 $\sqrt{2}$ ，E，F分别是AC，AB上的一点，若∠CFE=45°．若设AE=y，BF=x，求出y与x的函数关系及y的最大值．

(3)、【拓展提高】已知D是等边△ABC边AB上的一点，现将△ABC折叠，使点C与D重合，折痕为EF，点E，F分别在AC和BC上．如图3如果AD：BD=1：2，求CE：CF的值．

查看试题解析
24. 给出定义：有两个内角分别是它们对角的两倍的四边形叫做倍对角四边形．

(1)、如图1，在倍对角四边形ABCD中，∠D＝2∠B，∠A＝2∠C，求∠B与∠C的度数之和；

(2)、如图2，锐角△ABC内接于⊙O，若边AB上存在一点D，使得BD＝BO．∠OBA的平分线交OA于点E，连结DE并延长交AC于点F，∠AFE＝2∠EAF．
求证：四边形DBCF是倍对角四边形；

(3)、如图3，在（2）的条件下，过点D作DG⊥OB于点H，交BC于点G．当4DH＝3BG时，求△BGH与△ABC的面积之比．

查看试题解析

x	…	-1	0	1	2	3	…
y＝ax²+bx+c	…	12	5	2	5	14	…