浙江省宁波市镇海区蛟川书院2021-2022学年八年级上学期数学期中考试试卷

试卷更新日期：2021-12-07 类型：期中考试

进入 出卷网 下载

一、选择题：本题共10小题，每小题4分，共40分。

  • 1. 2021年是农历辛丑牛年，习近平总书记勉励全国各族人民在新的一年发扬“为民服务孺子牛、创新发展拓荒牛、艰苦奋斗老黄牛”精神，某社区也开展了“迎新春牛年剪纸展”，下面的剪纸作品是轴对称图形的是（   ）
    A、  B、 C、 D、

    查看试题解析

  • 2. 等腰三角形两条边长分别是6和8，则其周长为（   ）
    A、20 B、22 C、20或22 D、24

    查看试题解析

  • 3. 若a＞b，下列不等式不一定成立的是（   ）
    A、a﹣2021＞b﹣2021 B、﹣2021a＜﹣2021b    C、ac>bc D、a+c＞b+c

    查看试题解析

  • 4. 在平面直角坐标系中，点A（3，﹣2）所在的象限是（   ）
    A、一 B、二 C、三 D、四

    查看试题解析

  • 5. 根据下列条件不能判断△ABC是直角三角形的是（   ）
    A、∠A＝55°，∠B＝35° B、∠A：∠B：∠C＝7：4：3 C、AB＝3，BC＝4，CA＝ 7 D、AB＝m2﹣n2 ， BC＝4mn，AC＝m2+n2（m＞n＞0）

    查看试题解析

  • 6. 将直线y＝5x向下平移2个单位长度，所得直线的表达式为（   ）
    A、y＝5x﹣2 B、y＝5x+2 C、y＝5（x+2） D、y＝5（x﹣2）

    查看试题解析

  • 7. 直线y＝﹣2x+b上有三个点（- 2 ，y1），（﹣1.5，y2），（1.3，y3），则y1 ， y2 ， y3的大小关系是（   ）
    A、y1＞y2＞y3 B、y1＜y2＜y3 C、y2＞y1＞y3 D、y2＜y1＜y3

    查看试题解析

  • 8. 如图，已知∠AOB＝30°，点P在∠AOB内部，P1与P关于OB对称，P2与P关于OA对称，则P1 ， O，P2三点所构成的三角形是（   ）

    A、直角三角形 B、钝角三角形 C、等腰三角形 D、等边三角形

    查看试题解析

  • 9. 如图所示，有一块直角三角形纸片，∠C＝90°，AB＝5cm，BC＝3cm，将斜边AB翻折，使点B落在直角边AC的延长线上的点E处，折痕为AD，则CD的长为（   ）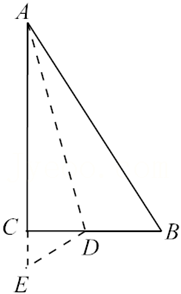

    A、1cm B、43 cm C、1.5cm D、53 cm

    查看试题解析

  • 10. 勾股定理是人类最伟大的科学发现之一，在我国古算书《周髀算经》中早有记载.如图以直角三角形的各边为边分别向同侧作正方形，若知道图中阴影部分的面积之和，则一定能求出（   ）

    A、正方形ABED的面积 B、正方形ACFG的面积 C、正方形BCMN的面积 D、△ABC的面积

    查看试题解析

二、填空题：本题共6小题，每小题5分，共30分。

  • 11. 函数y= x−1x−2 中，自变量x的取值范围是.

    查看试题解析

  • 12. 若一次函数y＝ax+b过第一、二、四象限，则y＝bx+a的图象不经过第象限.

    查看试题解析

  • 13. “等腰三角形两腰上的中线相等.”的逆命题是.

    查看试题解析

  • 14. 如果不等式组 {x+5<4x−1x>m 的解集是x＞2，则m的取值范围是.

    查看试题解析

  • 15. 如图，在△ABC中，AD平分∠BAC，BP⊥AD与点P，若∠ABC＝3∠C，则 AC−ABBP 的值为 .

    查看试题解析

  • 16. 如图，在△ABC中，∠ABC＝90°，∠C＝30°，点D是AC边上一动点（不与A、C重合），过点D作DE⊥AB于点E，联结BD，将△EBD沿直线BD翻折，点E落在点E′处，直线BE′与直线AC相交于点M，当△BDM为等腰三角形时，则∠ABD＝.

    查看试题解析

三、解答题：第17-19题各8分，第20题10分，第21题8分，第22、23题各12分，第24题14分，共80分

  • 17. 解下列不等式（组）：
    (1)、2x−13<3x−22 ﹣1；
    (2)、{3x−1≥x+1x+4>4x−2 .

    查看试题解析

  • 18. 如图，在△ABC中，AB＝AC，D是BC边的中点，过点D分别作DE、DF垂直AB、AC.

    (1)、求证：DE＝DF；
    (2)、若∠B＝30°，AE＝1，求BC.

    查看试题解析

  • 19. 已知y是关于x的一次函数，当x＝3时，y＝1，x＝﹣2时，y＝﹣14.
    (1)、求y关于x的函数解析式；
    (2)、当y≤2时，求x的取值范围.

    查看试题解析

  • 20. 如图，在平面直角坐标系中，A（﹣3，3），B（﹣4，4），C（0，﹣1）.

    ⑴在图中作出△ABC关于y轴对称的△A1B1C1 ， 并写出△A1B1C1顶点的坐标；

    ⑵求△ABC的周长；

    ⑶在x轴上求出点P坐标，使PB+PC最小.

    查看试题解析

  • 21. 如图，在△ABC中，∠BAC＝90°，延长CA至D使得CD＝BA，过D作DE⊥CD且满足CB＝CE，连接CE.

    (1)、求证：∠B＝∠DCE；
    (2)、延长BA交CE于点G，作∠BCA的平分线交AB于点F，若G为CE中点，连接EF，求∠EFC的度数.

    查看试题解析

  • 22. 某商店购进甲，乙两种商品，甲的进货单价比乙的进货单价高10元，已知20个甲商品的进货总价与30个乙商品的进货总价相同.
    (1)、求甲、乙商品的进货单价；
    (2)、若甲、乙两种商品共进货100件，甲商品按进价提高10%后的价格销售，乙商品按进价提高30%后的价格销售，若甲、乙两种商品全部售完，设甲商品进货x件，利润为y，求y关于x的函数关系式；
    (3)、在条件（2）下，要求两种商品全部售完后的销售总额不低于2950元，并且不再考虑其他因素，哪种方案利润最大？最大利润是多少？

    查看试题解析

  • 23. 定义：一次函数y＝ax+b和一次函数y＝﹣bx﹣a为“逆反函数”，如y＝3x+2和y＝﹣2x﹣3为“逆反函数”.
    (1)、点A（a，3）在y＝x+2的“逆反函数”图象上，则a＝；
    (2)、y＝4x+3图象上一点B（m，n）又是它的“逆反函数”图象上的点，求点B的坐标；
    (3)、若y＝﹣2x+b和它的“逆反函数”与y轴围成的三角形面积为3，求b的值.

    查看试题解析

  • 24. 如图，已知直线y＝﹣x+4与y轴交于点A，与x轴交于点B，过点C（1，0）作CD⊥x轴交直线AB于点D.点P是x轴上的一个动点，点E是BD的中点，在△PEF中（三顶点顺时针排列），∠PEF＝90°，PE＝EF.

    (1)、则A、B、D三点的坐标分别为：A ， B ， D.
    (2)、如图，当点P在线段CB上时，若CP＝2BP，求点F的坐标.
    (3)、当点P在射线CB上运动，连接AF.若S△AEF＝5S△PBE ， 求点P的坐标.

    查看试题解析