浙江省杭州市下城区2021-2022学年八年级上学期数学期中考试试卷
试卷更新日期：2021-12-07 类型：期中考试
一、选择题（每小题3分，共30分）
-
1. 做一个三角形的木架，以下四组木棒中，符合条件的是（ ）
A、3cm，2cm，1cm B、3cm，4cm，5cm C、5cm，12cm，6cm D、6cm，6cm，12cm2. 如果a＞b，那么下列结论一定正确的是（ ）A、a﹣3＜b﹣3 B、1+a＞1+b C、﹣3a＞﹣3b D、 ＜3. 等腰三角形的周长为9，一边长为4，则腰长为（ ）A、5 B、4 C、2.5 D、2.5或44. 根据下列已知条件，能唯一画出△ABC的是（ ）A、AB=3，BC=4，AC=8 B、AB=4，BC=3，∠A=30° C、∠A=60°，∠B=45°，AB=4 D、∠C=90°，AB=65. 不等式2x﹣6≤0的非负整数解的个数为（ ）A、1个 B、2个 C、3个 D、4个6. 如图，已知在△ABC中，CD是AB边上的高线，BE平分∠ABC，交CD于点E，BC＝5，DE＝2，则△BCE的面积等于（ ）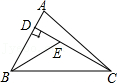
A、10 B、7 C、5 D、47. 如图，△ABC中，∠C＝90°，AB的中垂线DE交AB于E，交BC于D，若AB＝10，AC＝6，则△ACD的周长为（ ）
A、16 B、14 C、20 D、188. 下列命题：①成轴对称的两个三角形是全等三角形；②当a＞b时，若c＞0，则ac＞bc；③直角三角形中斜边上的中线等于斜边的一半；④内错角相等，其中原命题与逆命题均为真命题的个数是（ ）A、1个 B、2个 C、3个 D、4个9. 如图，在△ABC中，∠ACB＝90°，D在BC上，E是AB的中点，AD、CE相交于F，且AD＝DB.若∠B＝20°，则∠DFE等于（ ）
A、30° B、40° C、50° D、60°10. 如图，等腰Rt△ABC中，∠BAC＝90°，AD⊥BC于D，∠ABC的平分线分别交AC、AD于E、F两点，M为EF的中点，延长AM交BC于点N，连接DM.下列结论：①DF＝DN；③AE＝CN；③△DMN是等腰三角形；④∠BMD＝45°，其中正确的结论个数是（ ）
A、1个 B、2个 C、3个 D、4个二、填空题（每小题4分，共24分）
-
11. 请写出“等腰三角形的两底角相等”的逆命题：12. 如果不等式（b+1）x＜b+1的解集是x＞1，那么b的范围是 .13. 已知直角三角形的两条边长分别为6和8，那么该直角三角形斜边上的中线长是 ．14. 如图，∠ABC的平分线BF与△ABC的相邻外角∠ACG的平分线CF相交于F，过F作DF∥BC，交AB于D，交AC于E，若BD＝8cm，CE＝5cm，则DE的长为 .
15. 已知等腰△ABC，其腰上的高线与另一腰的夹角为35°，那么顶角为度数是.16. 如图，在Rt△ABC中，∠ABC＝90°，AB＝8，BC＝6，点D为直线AB上一动点，当BD＝时，△ADC为等腰三角形.
三、简答题（66分）
-
17. 解不等式，并把解集在数轴上表示出来.(1)、7x﹣2≤9x+2；(2)、1 .18. 如图所示，在△ABC中，AC＝8cm，BC＝6cm；在△ABE中，DE为AB边上的高，DE＝12cm，△ABE的面积S＝60cm2.
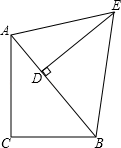(1)、求出AB边的长；(2)、你能求出∠C的度数吗？请试一试.19. 已知：如图，在△ABC中，AD平分∠BAC，BD＝CD，DE⊥AB于E，DF⊥AC于F.
(1)、求证：△ABC是等腰三角形.(2)、若AB＝13，BC＝10，求DE的长.20. 某校暑假准备组织该校的“三好学生”参加夏令营，由1名老师带队.甲旅行社说：“若老师买全票一张，则学生可享受半价优惠.”
乙旅行社说：“包括老师在内都6折优惠”
若全票价是1200元，则：
(1)、设三好学生人数为x人，则参加甲旅行社的费用是 1200+600x 元；参加乙旅行社的费用是元.(2)、当学生人数取何值时，选择参加甲旅行社比较合算？21. 如图，在△ABC中，AB＝AC ， D为BC上一点，∠B＝30°，连接AD ．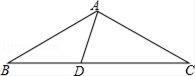
(1)、若∠BAD＝45°，求证：△ACD为等腰三角形；(2)、若△ACD为直角三角形，求∠BAD的度数．22. 如图，等腰直角三角尺△ABC与30°三角尺△ABD斜边AB重合，O为AB的中点，连接DC.
(1)、判断△OCD的形状；(2)、求∠COD的度数；(3)、若CO＝2，求△OCD的面积.23. 在△ABC中，AB＝AC，点D是直线BC上一点（不与B、C重合），以AD为一边在AD的右侧作△ADE，使AD＝AE，∠DAE＝∠BAC，连接CE.
(1)、如图1，当点D在线段BC上，如果∠BAC＝90°，则∠BCE＝度；(2)、设∠BAC＝α，∠BCE＝β.①如图2，当点D在线段BC上移动，则α，β之间有怎样的数量关系？请说明理由；
②当点D在直线BC上移动，则α，β之间有怎样的数量关系？请直接写出你的结论.