江苏省苏州市高新区新区2021年数学中考二模试卷
试卷更新日期:2021-12-07 类型:中考模拟
一、单选题
-
1. ﹣2021的相反数是( )A、﹣2021 B、2021 C、﹣ D、2. 中芯国际集成电路制造有限公司,是世界领先的集成电路晶圆代工企业之一,也是中国内地技术最先进、配套最完善、规模最大、跨国经营的集成电路制造企业集团,中芯国际第一代14纳米FinFET技术取得了突破性进展,并于2019年第四季度进入量产,代表了中国大陆自主研发集成电路的最先进水平,14纳米=0.000000014米,0.000000014用科学记数法表示为( )A、 B、 C、 D、3. 如图所示物体的左视图是( )
 A、
A、 B、
B、 C、
C、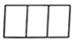 D、
D、 4. 校国旗班男生的身高如表:
4. 校国旗班男生的身高如表:身高
175
178
180
181
182
人数(名)
4
6
5
3
2
则这个国旗班20名男生身高的众数和中位数分别是( )
A、 B、 C、 D、5. 如图,点 、 、 在⊙O上, , ,则 的度数是( ) A、110° B、125° C、135° D、165°6. 如果解关于x的分式方程 时出现增根,那么m的值为( )A、-2 B、2 C、4 D、-47. 如图, 为等腰 内一点,过点 分别作三条边 、 、 的垂线,垂足分别为 、 、 ,已知 , ,且 ,则 的长为( )
A、110° B、125° C、135° D、165°6. 如果解关于x的分式方程 时出现增根,那么m的值为( )A、-2 B、2 C、4 D、-47. 如图, 为等腰 内一点,过点 分别作三条边 、 、 的垂线,垂足分别为 、 、 ,已知 , ,且 ,则 的长为( ) A、 B、 C、7 D、88. 使用家用燃气灶烧开同一壶水所需的燃气量 (单位: )与旋钮的旋转角度 (单位:度)( )近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度 与燃气量 的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为( )
A、 B、 C、7 D、88. 使用家用燃气灶烧开同一壶水所需的燃气量 (单位: )与旋钮的旋转角度 (单位:度)( )近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度 与燃气量 的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为( )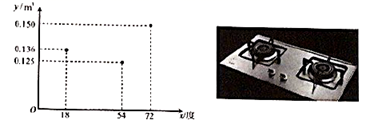 A、 B、 C、 D、9. 如图,直线 与双曲线 (k<0,x<0)交于点A,将直线 向上平移2个单位长度后,与y轴交于点C,与双曲线交于点B,若OA=2BC,则k的值为( )
A、 B、 C、 D、9. 如图,直线 与双曲线 (k<0,x<0)交于点A,将直线 向上平移2个单位长度后,与y轴交于点C,与双曲线交于点B,若OA=2BC,则k的值为( ) A、 B、-7 C、 D、10. 如图,矩形 中, ,以 为圆心,3为半径作 , 为 上一动点,连接 ,以 为直角边作 ,使 , ,则点 与点 的最小距离为( )
A、 B、-7 C、 D、10. 如图,矩形 中, ,以 为圆心,3为半径作 , 为 上一动点,连接 ,以 为直角边作 ,使 , ,则点 与点 的最小距离为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若 在实数范围内有意义,则x的取值范围是 .12. 计算 的结果等于.13. 设 是一元二次方程 两个根,则 .14. 若一个圆锥的底面半径为2,母线长为6,则该圆锥侧面展开图的圆心角是°.
15. 《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),则AB的长是寸. 16. 如图,抛物线 与直线 的两个交点坐标分别为 ,则方程 的解是.
16. 如图,抛物线 与直线 的两个交点坐标分别为 ,则方程 的解是.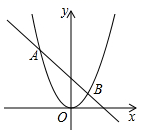 17. 如图,在正方形 外侧作直线 ,点 关于直线 的对称点为 ,连接 , .其中 交直线 于点 .若 ,则当 , 时,正方形 的边长为.
17. 如图,在正方形 外侧作直线 ,点 关于直线 的对称点为 ,连接 , .其中 交直线 于点 .若 ,则当 , 时,正方形 的边长为. 18. 在平面直角坐标系xOy中,已知点M,N的坐标为 , ,若抛物线 与线段MN有两个不同的交点,则a的取值范围是 .
18. 在平面直角坐标系xOy中,已知点M,N的坐标为 , ,若抛物线 与线段MN有两个不同的交点,则a的取值范围是 .三、解答题
-
19. 计算:(3﹣π)0﹣4cos30°﹣ +|1﹣ |.20. 解不等式组 并写出它的整数解21. 先化简,后求值:(1﹣ )÷ ,其中x= +3.22. 珠海市有A,B,C,D,E五个景区很受游客喜爱.对某小区居民在暑假期间去以上五个景区旅游(只选一个景区)的意向做了一次随机调查统计,并根据这个统计结果制作了如下两幅不完整的统计图.
 (1)、该小区居民在这次随机调查中被调查到的人数是人,m=;(2)、若该小区有居民1500人,试估计去C景区旅游的居民约有多少人?(3)、甲、乙两人暑假打算游玩,甲从B、C两个景点中任意选择一个游玩,乙从B、C 、E三个景点中任意选择一个游玩.求甲、乙恰好游玩同一景点的概率.23. 定义:一条对角线垂直平分另一条对角线的四边形叫做筝形,如图,筝形ABCD的对角线AC、BD相交于点O.且AC垂直平分BD.
(1)、该小区居民在这次随机调查中被调查到的人数是人,m=;(2)、若该小区有居民1500人,试估计去C景区旅游的居民约有多少人?(3)、甲、乙两人暑假打算游玩,甲从B、C两个景点中任意选择一个游玩,乙从B、C 、E三个景点中任意选择一个游玩.求甲、乙恰好游玩同一景点的概率.23. 定义:一条对角线垂直平分另一条对角线的四边形叫做筝形,如图,筝形ABCD的对角线AC、BD相交于点O.且AC垂直平分BD. (1)、请结合图形,写出筝形两种不同类型的性质:性质1:;性质2:.(2)、若AB∥CD,求证:四边形ABCD为菱形.24. 汉书《淮南万毕术》记载:取大境高悬,置水盆于下,则见四邻.如图1,这句话是说,利用高挂上面的镜子所成的像,再反射到水盆中,借此观察院墙外景象.相关光的路径和围墙等,用几何图形表示如图2,已知点 , , , 在同一条水平线上,点 在围墙 的正上方, 于点 , 于点 , , , 米, ,求点 到墙脚 的距离.(结果精确到0.1米.参考数据: , , , , , )
(1)、请结合图形,写出筝形两种不同类型的性质:性质1:;性质2:.(2)、若AB∥CD,求证:四边形ABCD为菱形.24. 汉书《淮南万毕术》记载:取大境高悬,置水盆于下,则见四邻.如图1,这句话是说,利用高挂上面的镜子所成的像,再反射到水盆中,借此观察院墙外景象.相关光的路径和围墙等,用几何图形表示如图2,已知点 , , , 在同一条水平线上,点 在围墙 的正上方, 于点 , 于点 , , , 米, ,求点 到墙脚 的距离.(结果精确到0.1米.参考数据: , , , , , )
 25. 某牧场准备利用现成的一堵“7”字型的墙面(如图中粗线 表示墙面,已知 , 米, 米)和总长为36米的篱笆围建一个“日”形的饲养场 (细线表示篱笆,饲养场中间 也是用篱笆隔开),如图,点 可能在线段 上,也可能在线段 的延长线上.
25. 某牧场准备利用现成的一堵“7”字型的墙面(如图中粗线 表示墙面,已知 , 米, 米)和总长为36米的篱笆围建一个“日”形的饲养场 (细线表示篱笆,饲养场中间 也是用篱笆隔开),如图,点 可能在线段 上,也可能在线段 的延长线上.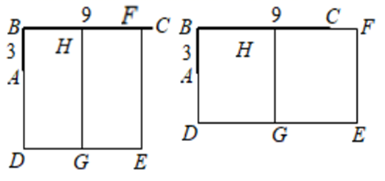 (1)、当点 在线段 上时,
(1)、当点 在线段 上时,①设 的长为 米,则 ▲ 米(用含 的代数式表示);
②若要求所围成的饲养场 的面积为66平方米,求饲养场的宽 ;
(2)、饲养场的宽 为多少米时,饲养场 的面积最大?最大面积为多少平方米?26. 如图,在 中, 是 边上的点,过点 作 交 边于点 ,垂足为 ,过点 作 ,垂足为 ,连接 ,经过点 , , 的 与边 另一个公共点为 . (1)、连接 ,求证 ;(2)、若 , , .
(1)、连接 ,求证 ;(2)、若 , , .①当 时,求 的半径;
②当点 在 边上运动时, 半径的最小值为 ▲ .
27. 如图1,抛物线 交 轴于 , 两点( 在 的左侧),与 轴交于点 ,且 .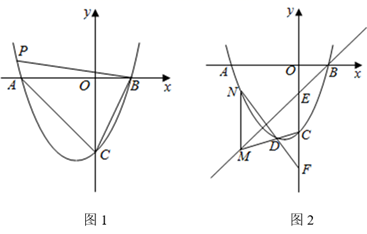 (1)、求抛物线的解析式;(2)、连接 , ,点 在抛物线上,且满足 ,求点 的坐标;(3)、如图2,直线 交 轴于点 ,过直线 上的一动点 作 轴交抛物线于点 ,直线 交抛物线于另一点 ,直线 交 轴于点 ,试求 的值.28. 定义:三角形一边上的点将该边分为两条线段,且这两条线段的积等于这个点到这边所对顶点连线的平方,则称这个点为三角形该边的“好点”.如图1, 中,点 是 边上一点,连接 ,若 ,则称点 是 中 边上的“好点”.
(1)、求抛物线的解析式;(2)、连接 , ,点 在抛物线上,且满足 ,求点 的坐标;(3)、如图2,直线 交 轴于点 ,过直线 上的一动点 作 轴交抛物线于点 ,直线 交抛物线于另一点 ,直线 交 轴于点 ,试求 的值.28. 定义:三角形一边上的点将该边分为两条线段,且这两条线段的积等于这个点到这边所对顶点连线的平方,则称这个点为三角形该边的“好点”.如图1, 中,点 是 边上一点,连接 ,若 ,则称点 是 中 边上的“好点”.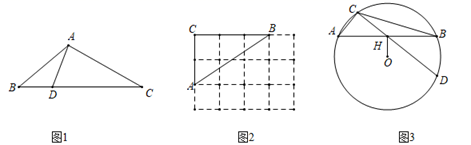 (1)、如图2, 的顶点是 网格图的格点,请仅用直尺画出(或在图中直接描出) 边上的“好点”;(2)、 中, , , ,点 是 边上的“好点”,求线段 的长;(3)、如图3, 是⊙O的内接三角形,点 在 上,连结 并延长交⊙O于点 .若点 是 中 边上的“好点”.
(1)、如图2, 的顶点是 网格图的格点,请仅用直尺画出(或在图中直接描出) 边上的“好点”;(2)、 中, , , ,点 是 边上的“好点”,求线段 的长;(3)、如图3, 是⊙O的内接三角形,点 在 上,连结 并延长交⊙O于点 .若点 是 中 边上的“好点”.①求证: ;
②若 ,⊙O的半径为 ,且 ,求 的值.